Методика дослідження, Процесс побудови математичної моделі за допомогою методу кінцевих різниць - Застосування комп'ютерно-інтегрованих систем в технології лиття
Процесс побудови математичної моделі за допомогою методу кінцевих різниць
У цій методиці дослідження ми опишемо один з найбільш універсальних методів вирішення графічних завдань. Метод кінцевих різниць - це один з найпоширеніших методів рішення. Цей метод часто використовують для задач в основі яких лежить диференціальне рівняння. Сама велика перевага цих методів в тому, що диференціальні рівняння до вирішення систем алгебраїчних рівнянь по відношенню використовуваної функції. У такому випадку це буде вироблено шляхом заміни похідних.
У даній роботі ми маємо лінійне диференціальне рівняння другого порядку, яке розглянемо за допомогою методу кінцевих різниць.

Де P(x),q(x),f(x) - відомі функції;
Таким чином граничні умови в загальному вигляді виражаються:



- задані постійні, причому виконується умова

.
Необхідно виконати наступні дії, щоб вирішити завдання (2.1) (2.2) (2.3) методом кінцевих різниць.
Для побудови сітки на відрізки (a, b) будуеться:

Вивести де - вузли сітки, I=0,1,...,n; точки и - це граничні вузли сітки, всі інші кути називаються внутрішніми. Потрібно замінити область безперервної зміни дискретною безліччю точок. Для вирішення завдання кількості та рішення вузлів сітки вибираємо в залежності від необхідної точності.

Величина I=0,1,...,n-1 називаеться кроеом сітки.

В даному випадку сітка вибирається рівномірно і крок сітки в цьому випадку вибирається як H=(b-a)/n.
Для того, щоб вирішити систему алгебраїчних рівнянь знадобиться замінити диференціальні рівняння (2.1) і граничні умови (2.2) (2.3) різницевими рівняннями:



1. Для цього, в кожному вузлів сітки i, визначимо сіткову функцію, також замінити значення похідної методом кінцевих різниць. Переходимо від безперервного диференціального рівняння, до різницевої задачі щодо сіткової функції ; які в підсумку замінюють граничну задачу (2.1) - (2.3) систем алгебраїчний рівнянь.

2. Необхідно вирішити систему алгебраїчних рівнянь щодо сіткової функції тим самим знайти таблицю значень цієї сіткової функції, що є наближеним рішенням вихідної крайової задачі. Необхідно вирішити систему алгебраїчних рівнянь щодо сіткової функції і тим самим знайти таблицю значень цієї сіткової функції, що є наближеним рішенням вихідної крайової задачі.
Є різні способи побудови кінцево - різницевих систем, але найпростішим з них з них є заміна функції у вузлах сітки.
Розкладань функції u (x) в ряд Тейлора можуть бути отримані такі співвідношення як: права різницева схема і ліва різницева схема з першим порядком апроксимації по h; центрально-різницева схема з другим порядком апроксимації по h.



У i-том вузлі сітки, похідну замінимо формулою другого різницевої похідної, з другим порядком апроксимації по h. (2.7)

Опис формули наведені для рівномірної сітки. Порядок апроксимуючих виразів буде залежати від розподілу вузлів сітки. Можемо припустити, що, для цього виберемо довільний вузол з номером i = 1,2, ..., n-1 і скористаємося співвідношеннями (2.6) і (2.7). Запишемо рівняння (2.1)

Наводимо подібні:

Де,



Для цього ми розповсюдили різницеве рівняння на всі внутрішні вузли сітки, так як вузол сітки вибирався довільно. для апроксимації другого порядку точності вибиралися звичайно-різницеві співвідношення, тобто. Припустимо, що, тобто апроксимуємо функцію правій частині. Для цього зобов'язані записати кінцево-різницеву апроксимацію для граничних умов (2.2) - (2.3).
Зі співвідношень (2.4) - (2.5), отримуємо:


Перетворимо:

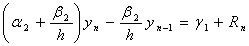
Звідси і. Можемо відкинути похибка апроксимації Ri, i = 0,1,2, ..., n при досить малих h і отримаємо кінцево-різницеву схему першогопорядку апроксимації по h.


Розглядаючи диференціальні рівняння (2.1) - (2.3) прийшли до рішення, що це система алгебраїчних рівнянь (2.15) - (2.17). Така система може бути як лінійної, так і нелінійної, залежно від того, яке вихідне диференціальне рівняння.

За нормою вектора судимо про близькості завдання (2.15)-(2.17) до вихідної задачі (2.1) - (2.3). Кажуть, що побудована різницева схема (2.15) - (2.17) апроксимує вихідну крайову задачу (2.1) - (2.3), якщо норма цього вектора || R || ®0 при H®0. Також при цьому виконується умова, тоді різницева задача (2.15) - (2.17) апроксимує вихідну диференціальну задачу (2.1) - (2.3). Маючи похибка першого порядку, граничні умови замінялися співвідношеннями першого порядку апроксимації по h. Досить замінити першу похідні на кінцях відрізка і для підвищення порядку апроксимації. Виходячи з цього, використовуємо наступні формули:


Для того, щоб знайти наближене рішення вихідні завдання (2.1) - (2.3) потрібно вирішити систему (2.15) - (2.17) які надають собою систему алгебраїчних рівнянь.
При використанні методу сіток алгоритм яких ми розглянемо, виникають часто такі питання:
- 1. Якими методами варто знаходити це рішення. 2. Якщо рішення системи алгебраїчних рівнянь, які ми описали (2.15) - (2.17).
Існує єдине рішення системи (2.15) - (2.17) так як вихідна задача (2.1) - (2.3) є лінійною, а система (2.15) (2.17) є трьох діагональною матрицею і при виконанні умови діагонального переважання рішення самої системи, існує і є єдиним, а таке рішення системи називається методом прогону.
Граничні умови є крайовими умовами першого роду, то при h>0 різницеве рішення рівномірно сходиться до точного зі швидкістю, так як Q(x)=0, а P(x), f(x) є двічі безперервно диференційованими функціями.
Дуже важливо провести розрахунки для різних значень кроку, не менше 3, після цього переконатися в тому, що в одних і тих же вузлах значення близькі між собою. ливарний комп'ютерний виливка корпус
На основі звичайного диференціального рівняння другого порядку для нелінійної задачі розглядається питання її апроксимації, також досліджується питання про похибки такої апроксимації, порядку. Для того щоб не виникало труднощів з розрахунками то потрібно провести розрахунок на декількох сітках з різними кроками. Якщо різницеві рішення близькі між собою, то це є свідченням гарної стійкості.
Похожие статьи
-
Комп'ютерне моделювання стає невід'ємною частиною процесів конструювання нових деталей і проектування технологічних процесів їх виготовлення. Воно...
-
Вступ - Застосування комп'ютерно-інтегрованих систем в технології лиття
Актуальність комп'ютерно-інтегрованих технологій, для виготовлення деталей, займає дуже важливе місце в світі. На заході вже протягом багатьох років...
-
Методы настройки двухсвязных систем регулирования - Автоматические регуляторы
Из общего числа систем регулирования около 15% составляют двухсвязные системы регулирования (рис.11). В таких системах даже при наличии устойчивой...
-
При создании и эксплуатации автоматических систем необхо-димо стремиться обеспечить заданную, а иногда и максимальную надежность системы при...
-
Векторная схема и вывод векторного уравнения задачи прицеливания Векторная схема задачи прицеливания при стрельбе из авиационного артиллерийского оружия...
-
ПОВЫШЕНИЕ НАДЕЖНОСТИ СИСТЕМ ПРИ ЭКСПЛУАТАЦИИ. - Надежность систем автоматизации
Если в результате проектирования нерезервированной системы не удается обеспечить требуемую безотказность, можно применять следующие методы повышения...
-
Метод акустической эмиссии - Диагностика газораспределительных трубопроводов
Метод акустической эмиссии относится к диагностике и направлен на выявление состояния предразрушения трубоопровода путем определения и анализа шумов,...
-
В зависимости от числа постов для данного вида ТО и уровня их специализации различают два основных метода организации работ по техническому обслуживанию...
-
В инженерной практике принято промышленные холодильные камеры описывать линейным дифференциальным уравнением 1-го порядка с постоянными коэффициентами....
-
Общие рекомендации по повышению прогнозируемой надежности блока согласования каналов сводятся к следующему: - Для выявления ранних отказов необходимо...
-
Передаточную функцию системы по задающему воздействию - главную передаточную функцию получаем следующим образом: Передаточная функция системы по...
-
Класс в Rational Rose -- это описание общей структуры (данных и связей) для дальнейшего создания объектов. Для того чтобы генератор Rational Rose имел...
-
После описания звеньев системы определяем ее передаточную функцию, которая представляет собой произведение всех ПФ звеньев: (2.10) Подставляем в...
-
Описание задачи проектирования Данная система предназначена для установки "Cannon Viking Maxfoam", которая в свою очередь предназначена для производства...
-
Выбор метода организации технологического процесса на объекте проектирования Основные задачи, которые ставятся перед инженерно-технологической службой...
-
Цели метода конструирование, в конечном счете, следующие: - получение более лучших и более экономичных изделий; - рационализация и создание предпосылки...
-
Система автоматизированной оценки эффективности тепловых процессов влажно-тепловой обработки
Введение На современном этапе развития легкой промышленности большое внимание уделяется улучшению уровня качества выпускаемой продукции и повышению...
-
Методика приготовления опытных сплавов Для приготовления опытных сплавов использовалась электрическая печь сопротивления шахтного типа мощностью 10 КВт с...
-
При разработке проекта автоматизации в первую очередь необходимо решить вопросы выбора структуры управления. Под структурой управления понимается...
-
Системы автоматизированного проектирования (САПР) в настоящее время являются во многих случаях единственно возможными методами при конструировании новых...
-
Введение - Методология создания сложных технологических систем
Современный системный анализ - прикладная наука, которая ориентирована на прояснение причин возникновения проблем и на формирование вариантов их...
-
Основным технологическим средством автоматизации проектирования в машиностроении является цифровая ЭВМ, оперирующая с информацией, представленной в...
-
Введение - Разработка системы поверки манометров
Одной из главных форм государственного метрологического надзора и ведомственного контроля, направленных на обеспечение единства измерений в стране, как...
-
Анализ проблемы - Выбор варианта автоматизации процесса конструирования
Рассматривая появление новых технических изделий на рынке, пусть это будет сравнительно простой технический предмет потребления или сложная...
-
При выполнении данной работы была спроектирована система автоматизированного управления установкой для нейтрализации азотной кислоты аммиаком. Была...
-
Технология - это лесенка, ведущая к намеченной цели. Современный изобретатель фильтрует варианты, отбрасывая то, что кажется ему неудачным. Увеличение...
-
Экспериментальные методы настройки регулятора - Автоматические регуляторы
Для значительного числа промышленных объектов управления отсутствуют достаточно точные математические модели, описывающие их статические и динамические...
-
В ходе данной работы необходимо установить свойства системы автоматического управления, определить ее временные и частотные характеристики, а также...
-
Системный подход позволяет найти оптимальное, в широком смысле, решение задачи Проектирования за счет всестороннего, целостного рассмотрения, как...
-
Введение - Цифровая система автоматического регулирования температуры воды в баке
Проблема автоматизации в различных отраслях народного хозяйства является в настоящее время одной из ключевых и ее решение относится к одному из...
-
Краткие сведения об источниках и системах водоснабжения, очистке воды - Инженерные сети
Системы питьевого водоснабжения должны обеспечивать водопотребление на: -- питьевые и хозяйственные нужды населения (в жилых зданиях, на общественных...
-
Кучное биовыщелачивание - Кучное биовыщелачивание
Кучное биовыщелачивание -- способ переработки химическим или бактериальным выщелачиванием попутно добытых забалансовых и бедных балансовых...
-
Спечені алюмінієві сплави (САС) отримують брикетуванням, спіканням і деформацією порошків алюмінію та легуючих елементів або порошків стандартних...
-
Модель системы в надсистеме (МСН): Модель системы представляет собой графическое отражение основных элементов подсистемы, в которую входит изучаемый...
-
В процессе копчения происходит реакция между функциональными группами белков и отдельными составными частями дыма. О взаимодействии компонентов дыма с...
-
Для анализа кристаллизационного процесса был выполнен ДТА сплавов системы Al - Si с содержанием Si: 0.25, 0.5, 1.0, 3.0 и 5.0 %. Основные параметры...
-
Для подтверждения данных, полученных методом исследования опытных сплавов по кольцевой пробе, был использован метод дифференциального термического...
-
Проверяем пригодность роликоподшипников конических однорядных по ГОСТ 333-79, условное обозначение - 7202. Проверим пригодность подшипника по [8;c.103]:...
-
Комп'ютерні дослідження процесу піноутворення у рідинно-газовому пристрої ежекційного типу
Вступ Освоєння свердловин - комплекс робіт з викликання припливу пластового флюїду із продуктивних пластів на поверхню з метою досягнення проектної...
-
Системный анализ многоуровневых иерархических структур Современный этап развития автоматизации производства характеризуется внедрением сложных систем...
Методика дослідження, Процесс побудови математичної моделі за допомогою методу кінцевих різниць - Застосування комп'ютерно-інтегрованих систем в технології лиття