Параллельный алгоритм выделения дольного графа - Многокритериальная постановка задачи выбора проектов целевых программ

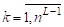
Рассмотрим взвешенный предфрактальный граф, порожденный затравкой и K процессоров, где.

Параллельный алгоритм выделения дольного графа основан на процедуре, которая выделяет двудольный граф, состоящий из двух частей.

Процедура состоит из двух шагов.

На первом шаге выделяем максимальное паросочетание максимального веса (МПМВ) используя алгоритм, предложенный Эдмондсом [7].

Второй шаг состоит в следующем.

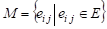
В МПВП входят множество ребер. Разобьем вершины на множества по принципу: одну вершину, инцидентную ребру включим во множество, другую - во множество, оставшиеся вершины графа включим во множество. Множества и выделенное множество ребер задают некоторый двудольный граф. Ребра, инцидентные вершинам множества и, инцидентные вершинам удаляем.

Множество вершин объединяем с множеством или двудольного графа по принципу:

    1. Eсли все вершины смежны с вершинами только множества или только множества, то множество вершин объединяем с множеством или множеством соответственно. При этом инцидентные им ребра сохраняем. 2. Вершины могут быть смежны с вершинами и множества и множества. Тогда считаем сумму весов ребер, инцидентных этой вершине, смежных с вершинами множества и аналогичную сумму соответственно для множества. Выбираем ребра, суммарный вес которых максимален. Включая эти ребра в двудольный граф, получая тем самым новый двудольный граф, определяем принадлежность этих вершин к долям.

Опишем принцип работы алгоритма.

Количество процессоров равно количеству всех затравок L-ого ранга, то есть. Тогда каждый из процессоров назначим одной из затравок, .

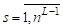
Каждая подграф-затравка, рассматривается как отдельно взятый граф. Все процессоров параллельно независимо друг от друга находят двудольный граф, каждый на назначенной ему затравке. Поиск двудольного графа на отдельно взятой подграф-затравке осуществляется с помощью процедуры. Далее каждую подграф-затравку

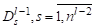
, стягиваем в одну вершину. Тогда мы получаем новый предфрактальный граф Аналогично предыдущему шагу, каждый процессор назначаем на одну из затравок. Аналогично, применяя процедуру находим двудольный граф. Общий тый шаг работы алгоритма представляет собой выделение двудольных графов. на затравках, .

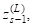
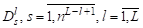
Далее на предфрактальном графе работа алгоритма на каждом том шаге заключается в объединении выделенных двудольных графов по принципу смежности вершин. Объединение двудольных графов будем обозначать.

Алгоритм заканчивает свою работу на м шаге, когда на последней исходной затравке выделяем двудольный граф. Тем самым, объединив все выделенные двудольные затравки на всех шагах работы алгоритма, получим дольный граф.

АЛГОРИТМ

Вход: взвешенный предфрактальный граф.

Выход: дольный граф

ШАГ 1. Параллельно и независимо друг от друга процессоров для каждой затравки, находят двудольный граф с помощью процедуры. На шаге 1 получаем двудольный граф максимальной затравки.

Шаг 2. Объединяя эти двудольные графы получаем покрытие предфрактального графа двудольными графами, которое дает в объединении дольный граф.

Процедура.

Вход: взвешенный предфрактальный граф.

Выход: двудольный граф.

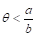
Теорема 1. Алгоритм Выделяет Дольный Граф () на предфрактальном - Графе , Порожденном Затравкой , , , С Коэффициентом Подобия .

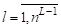
Доказательство. На первом шаге процессоров находят двудольные графы, используя процедуру.

На последнем шаге построения предфрактального графа все вершины замещаются затравкой, тогда каждая вершина - ого ранга принадлежит какой-либо подграф-затравке. Найдя двудольный граф на затравке, покроем все вершины, принадлежащие этой затравке.

Таким образом, на том шаге процессоры с помощью процедуры выделили двудольные графы на всех затравках.

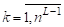
Дальнейшая работа алгоритма: на шаге используя те же процессоры, закрепляя их затравках предпоследнего ранга, применяя процедуру к каждой затравке, опять получим двудольный граф. Будем помнить, что каждая вершина этой затравки содержит внутри себя двудольный граф. Тогда если мы развернем эти двудольные графы, находящиеся внутри затравки, то у нас в покрытии получатся 4х - дольные графы. Продолжая этот процесс, на том шаге () получаем, что, на затравках применяя тот же принцип распределения процессоров и процедуру, опять получаем двудольные графы. Тогда на последнем шаге будет выделена последняя двудольная затравка и, объединяя выделенные затравки мы получим дольный граф (). Тем самым мы доказали, что алгоритм выделяет дольный граф. <

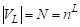
Теорема 2. Вычислительная сложность параллельного алгоритма выделения дольного графа () на предфрактальном - графе, порожденном затравкой, ,, где, равна.

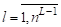
Доказательство. Алгоритм представляет собой, по существу многократное выполнение шага 1, т. е. поиск двудольного графа для каждой подграф-затравки, а их. Шаг 1 потребует выполнения операций на каждой подграф-затравке - столько операций выполняет алгоритм Эдмондса.

Тогда. Таким образом, вычислительная сложность алгоритма равна.

Сравнив вычислительную сложность параллельного алгоритма с вычислительной сложностью алгоритма Эдмондса, получим: , то есть ускорение вычисления параллельного алгоритма относительно алгоритма Эдмондса ~ . <

Примечание 1. Вычислительная Сложность Параллельного Алгоритма Меньше Вычислительной Сложности Алгоритма Эдмондса, В Раз На Предфрактальном - Графе . <

Теорема 3. Временная сложность параллельного алгоритма, где имеется процессоров, , равна.

Доказательство. Алгоритм выполняет шаг 1 параллельно, каждым из процессоров. Для выполнения шага 1 потребуется [7] времени (столько времени требуют процедура Эдмондса). Но все процессоры работают параллельно, то есть они закончат свою работу: "выполнение шага 1" в худшем случае за время. Таким образом, временная сложность алгоритма равна. <

Сравнив временную сложность параллельного алгоритма с вычислительной сложностью алгоритма Эдмондса, получим: .

Примечание 2. Временная Сложность Параллельного Алгоритма Меньше Временной Сложности Алгоритма Эдмондса, В Раз. <

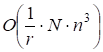
Теорема 4. Временная сложность параллельного алгоритма, где используется процессоров, , равна.

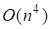
Доказательство. Алгоритм выполняет шаг 1 параллельно, каждым из процессоров. Для выполнения шага 1 требуется времени. Но все процессоры работают параллельно, т. е. все процессоров закончат свою работу: "выполнение шага 1" - одновременно, за время. Шаг 1 будет выполнен ровно раз. Тогда, получим:

.

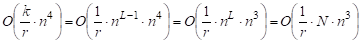
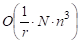
Получаем, что временная сложность алгоритма в случае использования процессоров, равна. <

Примечание 3. Временная Сложность Параллельного Алгоритма , Где Используется Процессоров , , Меньше Временной Сложности Алгоритма Эдмондса, В Раз. <

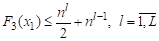
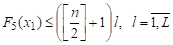
Теорема 5. Алгоритм выделяет покрытие на предфрактальном - графе, порожденном полной вершинной затравкой, ,, оптимальное по критериям и оцениваемое по третьему и пятому. (целая часть числа )

Доказательство. Доказательство оптимальности по критерию следует из структуры работы алгоритма. Алгоритм выделяет один дольный граф, то есть состоит из одной компоненты.

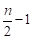
Для того, чтобы доказать оптимальность по критерию покажем, что на полном графе максимальное число ребер выделенного двудольного графа достигается, если доли равны (в случае, если делится пополам) или же доли будут равны и (если не делится пополам).

Для доказательства этого утверждения сформулируем и докажем предложение.

Предложение. Двудольный Граф На Графе , , Будет Наибольшим По Количеству Ребер, Если

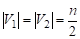
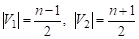
(в Случае, Когда Четно) И Если (в Случае, Когда Нечетно).

Доказательство. Докажем первую часть предложения.

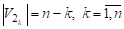
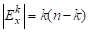
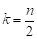
Если - четно, обозначим, тогда и максимальное количество ребер достигается при.

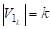
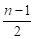
Если - нечетно, то одну вершину выделяем в сторону. Тогда число вершин четно и доли должны быть равны. Так как рассматриваем полный граф, то эту вершину относим в одну из долей и получаем максимальное число ребер. <

На основании доказанного предложения на каждой затравке алгоритм выделяет максимальное число ребер. На основании полученного результата и работы алгоритма на всех затравках на шаге 1, выделяется наибольшее количество ребер.

Аналогично рассуждая, видим, что на каждом шаге алгоритм выделяет максимальное число ребер, что доказывает оптимальность критерия.

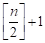
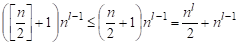
Дадим оценку. Согласно нашей модели, главными исполнителями является одна из долей выделенного двудольного графа. Максимальное число долей выделенного двудольного графа на затравке будет равна, а количество всех затравок на последнем шаге равноТогда общее количество исполнителей будет меньше либо равно.

Для оценки критерия последовательно оценим результат критерия по шагам работы алгоритма.

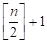
На первом шаге работы алгоритма, максимальная степень выделенного двудольного графа на затравке будет равна. На каждом алгоритм не запрещает увеличение степени вершины на. Аналогично рассуждая, на м шаге максимальная степень вершины может достичь.<

Похожие статьи




Параллельный алгоритм выделения дольного графа - Многокритериальная постановка задачи выбора проектов целевых программ

Предыдущая | Следующая