Прогнозирование сезонных колебаний объема перевозок - Статистика грузового автотранспортного предприятия
В статистике важной задачей является анализ и прогнозирование сезонной неравномерности перевозок. Отрицательно сказываются сезонная неравномерность на экономических показателях работы предприятия. Анализ необходим для оперативного планирования, для рациональной работы. Статистика ставит перед собой задачуопределить сезонные колебания и установить их размеры. Выявить наличие сезонных колебаний можно, построив график изменения среднесуточного объема перевозок по месяцам (рис. 19). Изменяются сезонные колебания при помощи индексов сезонности
IC = (QI/Q0) * 100 %,
Где QI - среднесуточный объем перевозок в i-ом месяце, т; Q0 - общее среднее значение объема перевозок за исследуемый период, т.
Среднесуточный объем перевозок в i-ом месяце
QI=QM/ДК, Т,
QI 2013=5745/31=185,32, т;
QI 2014=6105/31=196,94, т;
QI 2015=6527/31=210,55, т.
Дальнейшие расчеты сведены в табл. 19.
Общее среднее значение объема перевозок за исследуемый период
Q0= (QI 2013+QI 2014+ QI 2015) /12, т,
Q0= (3615,68+3804,32+3985,15) /12=316,81, т;
IC1= (197,6/316,81) *100%=62,37, %.
Дальнейшие расчеты сведены в табл. 19.
Таблица 19
Среднесуточные объемы перевозок и индексы сезонности
|
Месяцы |
Среднесуточный объем перевозок, т |
IС,% | |||
|
2013 |
2014 |
2015 |
Q | ||
|
1 |
185,32 |
196,94 |
210,55 |
197,60 |
62,37 |
|
2 |
258,93 |
282,50 |
295,29 |
278,90 |
88,04 |
|
3 |
278,52 |
264,71 |
250,87 |
264,70 |
83,55 |
|
4 |
293,07 |
317,73 |
341,53 |
317,44 |
100, 20 |
|
5 |
302,42 |
323,87 |
321,42 |
315,90 |
99,71 |
|
6 |
364,50 |
375,47 |
358,23 |
366,07 |
115,55 |
|
7 |
314,68 |
322,90 |
316,45 |
318,01 |
100,38 |
|
8 |
326,13 |
350,16 |
372,03 |
349,44 |
110,30 |
|
9 |
358,50 |
335,93 |
361,93 |
352,12 |
111,15 |
|
10 |
367,10 |
407,10 |
442,65 |
405,61 |
128,03 |
|
11 |
316, 20 |
361,43 |
376,23 |
351,29 |
110,88 |
|
12 |
250,32 |
265,58 |
337,97 |
284,62 |
89,84 |
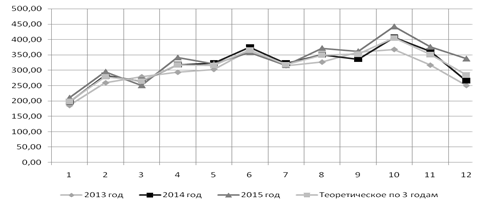
Рис. 22. Изменение среднесуточного объема перевозок по месяцам за 2013, 2014 и 2015 год
График иллюстрирует сезонную неравномерность объема перевозок, на котором видно, что несмотря на некоторые несущественные изменения объема перевозок от года к году, максимальные и минимальные объемы перевозок приходятся на одни и те же месяцы.
На январь приходятся самые низкие значения объемов перевозок. Это может быть связано с уменьшением количества заказов на перевозку и уменьшение количества рабочих дней в году.
Самые высокие значения приходятся на октябрь, это связано с большим числом заказов.
Для анализа и прогнозирования сезонных колебаний используется метод установления гармоник ряда Фурье:
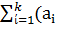
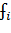
Yt= Q0 + *sin 2Пt +bI*cos 2Пt), т,
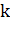
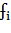
Где Q0 - Среднее значение исследуемого ряда динамики (среднемесячный объем перевозок); a и b - гармонические коэффициенты ряда Фурье; - номер гармоники, определяющий степень точности модели; - частота гармоник, определяющаяся:
=i/n,
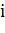
Где n - объем выборки; (=1...4)
Aиb определяют методом наименьших квадратов:
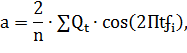
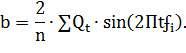
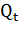
Где n - число месяцев в году; - исходный исследуемый ряд динамики (фактические месячные объемы перевозок)
Анализ неравномерности месячных объемов перевозок грузов проводится при k=1 и k=2.
Отклонение значения месячного объема перевозок от среднемесячного за год определяется
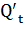
=QT-Q0, т,
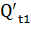
=197,6-316,81=-119,21, т;
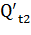
=278,9-316,81= - 37,91, т;
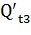
=264,7-316,81= - 52,11, т.
Все рассчитанные значения отклонений представлены в табл. 20.
Таблица 20
|
QT |
Q0 | |
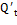
197,60 |
316,81 |
-119,21 |
|
278,90 |
316,81 |
-37,91 |
|
264,70 |
316,81 |
-52,11 |
|
317,44 |
316,81 |
0,63 |
|
315,90 |
316,81 |
-0,91 |
|
366,07 |
316,81 |
49,26 |
|
318,01 |
316,81 |
1, 20 |
|
349,44 |
316,81 |
32,63 |
|
352,12 |
316,81 |
35,31 |
|
405,61 |
316,81 |
88,80 |
|
351,29 |
316,81 |
34,48 |
|
284,62 |
316,81 |
-32, 19 |
Гармонические коэффициенты ряда Фурье:
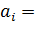
2/12* (-145,55) =-24,26
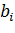
=2/12* (-302,65) =-50,44
Гармоническая функция при k=1:
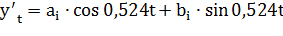
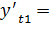
(-24,26) *0,866+ (-50,44) *0,500= - 46,23
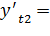
(-24,26) **0,499+ (-50,44) **0,866= - 55,79
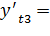
(-24,26) ** (-0,001) + (-50,44) **0,999= - 50,37
Рассчитанные значения представлены в табл.21.
I. Определение искомой теоретической кривой
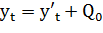
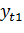
=-46,23+316,81=308,2
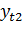
=-55,79+316,81=298,64
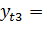
-50,37+316,81=304,065
Рассчитанные значения представлены в табл.21.
Таблица 21
Расчет значений теоретической функции (yT) при k=1
|
Месяцы |
Объемы перевозок, тонны (QT) |
Объем перевозок после вычитания среднемесячного значения (Q'T) |
Cos (0,524*t) |
Sin (0,524*t) |
Q'T * cos (0,524*t) |
Q'T * sin (0,524*t) |
Y'T, т. |
YT, т. |
|
1 |
197,6 |
-119,2 |
0,866 |
0,500 |
-103,236 |
-59,605 |
-46,229 |
270,581 |
|
2 |
278,9 |
-37,91 |
0,499 |
0,866 |
-18,917 |
-32,830 |
-55,787 |
261,023 |
|
3 |
264,7 |
-52,11 |
-0,001 |
0,999 |
0,052 |
-52,058 |
-50,365 |
266,445 |
|
4 |
317,44 |
0,63 |
-0,501 |
0,865 |
-0,316 |
0,545 |
-31,476 |
285,334 |
|
5 |
315,9 |
-0,91 |
-0,867 |
0,498 |
0,789 |
-0,453 |
-4,086 |
312,724 |
|
6 |
366,07 |
49,26 |
-0,999 |
-0,002 |
-49,211 |
-0,099 |
24,337 |
341,147 |
|
7 |
318,01 |
1,2 |
-0,865 |
-0,502 |
-1,038 |
-0,602 |
46,306 |
363,116 |
|
8 |
349,44 |
32,63 |
-0,497 |
-0,868 |
-16,217 |
-28,323 |
55,839 |
372,649 |
|
9 |
352,12 |
35,31 |
0,003 |
-0,999 |
0,106 |
-35,275 |
50,317 |
367,127 |
|
10 |
405,61 |
88,8 |
0,503 |
-0,864 |
44,666 |
-76,723 |
31,377 |
348,187 |
|
11 |
351,29 |
34,48 |
0,868 |
-0,496 |
29,929 |
-17,102 |
3,961 |
320,771 |
|
12 |
284,62 |
-32, 19 |
0,999 |
0,004 |
-32,158 |
-0,129 |
-24,438 |
292,373 |
|
Итого |
3801,719 |
- |
0,008 |
0,001 |
-145,550 |
-302,654 |
- |
- |
Таблица 22
Расчет значений теоретической функции (yT) при k=2
|
Месяцы |
Объемы перевозок, тонны (QT) |
Объем перевозок после вычитания среднемесячного значения (Q'T) |
Cos (1,047 *t) |
Sin (1,047*t) |
Q'T * cos (1,047*t) |
Q'T * sin (1,047*t) |
Y'T, т. |
YT, т. |
|
1 |
197,6 |
-119,2 |
0,500 |
0,866 |
-59,605 |
-103,236 |
-34,357 |
282,453 |
|
2 |
278,9 |
-37,91 |
-0,499 |
0,873 |
18,917 |
-33,095 |
-26,163 |
290,647 |
|
3 |
264,7 |
-52,11 |
-0,999 |
0,022 |
52,058 |
-1,146 |
7,672 |
324,482 |
|
4 |
317,44 |
0,63 |
-0,500 |
-0,851 |
-0,315 |
-0,536 |
33,835 |
350,645 |
|
5 |
315,9 |
-0,91 |
0,499 |
-0,883 |
-0,454 |
0,804 |
26,511 |
343,321 |
|
6 |
366,07 |
49,26 |
0,999 |
-0,043 |
49,211 |
-2,118 |
-6,941 |
309,869 |
|
7 |
318,01 |
1,2 |
0,501 |
0,840 |
0,601 |
1,008 |
-33,461 |
283,349 |
|
8 |
349,44 |
32,63 |
-0,498 |
0,893 |
-16,250 |
29,139 |
-26,868 |
289,942 |
|
9 |
352,12 |
35,31 |
-0,999 |
0,065 |
-35,275 |
2,295 |
6,176 |
322,986 |
|
10 |
405,61 |
88,8 |
-0,502 |
-0,828 |
-44,578 |
-73,526 |
33,052 |
349,862 |
|
11 |
351,29 |
34,48 |
0,498 |
-0,903 |
17,171 |
-31,135 |
27,216 |
344,026 |
|
12 |
284,62 |
-32, 19 |
0,999 |
-0,086 |
-32,158 |
2,768 |
-5,445 |
311,365 |
|
Итого |
3801,719 |
- |
-0,001 |
-0,035 |
-50,676 |
-208,780 |
- |
- |
Гармонические коэффициенты ряда Фурье:
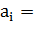
2/12* (-50,676) = - 8,446;
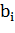
=2/12* (-208,78) = - 34,797.
Гармоническая функция при k=2 принимает вид
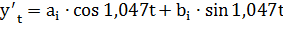
.
Значения представлены в табл.22.
Определение искомой теоретической кривой:
Значения представлены в табл.22
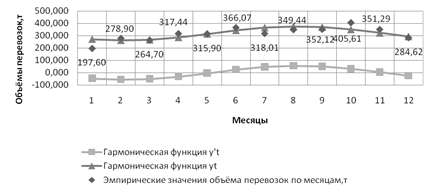
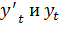
Рис. 23. График гармонических функций: при k = 1

Рис. 24. График гармонических функций: при k = 2
Рассчитываем корреляционное отношение (k=1):
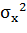
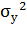
=14398,231=33214, 205
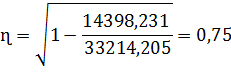
Это свидетельствует о относительно высокой степени корреляции.)
Стандартная ошибка аппроксимации:
, т.
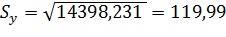
Похожие статьи
-
Соблюдение планового ритма перевозок на любом транспортном предприятии способствует выполнению плана, поэтому должно подвергаться постоянному...
-
Прогнозирование годового объема перевозок По динамике объема перевозок грузов и грузообороту можно сделать анализ, который служит для обоснования планов...
-
Контроль за выполнением плана по перевозкам - Статистика грузового автотранспортного предприятия
При изучении перевозок грузов и пассажиров статистика прежде всего определяет объемные и качественные показатели по перевозкам за отчетный период по...
-
Все процессы производства, в том числе и транспортный, планируются, измеряются и оцениваются с помощью определенной системы показателей и измерителей....
-
Введение - Статистика грузового автотранспортного предприятия
Успешная работа отраслей производственной инфраструктуры, а в первую очередь работа грузового транспорта, отражает свое влияние на задачах экономического...
-
Заключение - Статистика грузового автотранспортного предприятия
В курсовом проекте были проведены статистический анализ и оценка производственно-хозяйственной деятельности ГАТП. По полученным данным, можно сказать,...
-
Для определения влияния различных факторов на изменение грузооборота применяют последовательно-цепной индексный метод. Развернутая модель формирования...
-
Оценка эффективности работы предприятия - Статистика грузового автотранспортного предприятия
Статистическое изучение подразумевает уровень эффективности, характеристику его динамики и определяет факторы, обеспечивающие динамику. Понятия:...
-
Расчет фонда заработной платы водителей Р 1 2 3 4 5 6 7 8 9 Т. к 1,0 1,36 1,69 1.91 2,16 2,44 2,76 3,12 3,53 За месяц 33120 37440 №п/п Должность, вид...
-
Статистические методы изучения сезонных колебаний - Программа статистического наблюдения
Изучение сезонных колебаний проводится с целью выявления закономерно повторяющихся различий в уровне рядов динамики в зависимости от времени года. Так,...
-
Анализ сезонных колебаний динамического ряда - Ряды динамики
Расчет индексов сезонности 1) по способу переменной средней Расчет индексов сезонности объема розничной торговли проводим по формуле: I Sij = Х Ij / Х Р...
-
Годовой объем работ T2=(N*L*t(3))/1000 T2 - годовой объем работ, N - Число обслуживаемых авто-1500, L - Среднегодовой пробег авто-20000, T - Удельная...
-
Перечень профессий работников и их разряды. Наименование профессии Диапазон разрядов Слесарь-ремонтник 4 Слесарь по ремонту автомобилей 5 Машинист...
-
Расчет производственной программы ТО и ТР Наименование Показателей Показатели. Обозначение Норматив Ные Скорректирован Ные Принятые к расчету Годовой...
-
Годовой план заработной платы представляет собой сумму выплат работникам данного участка за год. Расчет фонда заработной платы ремонтных рабочих....
-
На основании данных годового отчета можно сравнить показатели объема производства товарной продукции и реализации в прошлом и отчетном году. Группировку...
-
3.1 Разработка проекта по повышению эффективности хозяйственной деятельности исследуемого предприятия ОАО "ПБТФ" намерено приобрести новую...
-
Платежеспособность -- это возможность предприятия расплачиваться по своим обязательствам. Предприятие является платежеспособным даже, когда свободных...
-
Расчет стоимости здания Фср. г = S x Ц S - Площадь здания - 1035, Ц - Цена за м2 20000, Фср. г = 1030х20.000. Стоимость здания =20.600.000 руб. Стоимость...
-
Существует два основных вида стимулирования торгового персонала в розничной организации с целью увеличение объемов продаж: - материально-денежное...
-
Плановая - расчетная цена - Показатели работы автотранспортного предприятия
Сводный расчет себестоимости транспортных услуг по маркам автомобилей: №п/п Статьи расходов ТАТРА TI58 руб MAN TGS руб. 1 Зарплата водителей с соц....
-
Мероприятия по повышению эффективности стимулирования торгового персонала розничной организации с целью увеличения объема В ОАО "Магнит" встречается...
-
Расчет себестоимости 1 часа обслуживания - Показатели работы автотранспортного предприятия
Себестоимость - все затраты на производство и реализацию продукции (услуг) Калькуляция - расчет себестоимости единицы продукции. Все расходы на...
-
Показатели производительности труда Основной экономической категорией, которая характеризует эффективность использования трудовых ресурсов, является...
-
С процессуальной точки зрения управление затратами предприятия начинается с планирования. Именно на стадии планирования определяются цели управления, как...
-
Построение аналитической группировки по уровню производительности труда работников в отрасли животноводства по хозяйствам Южной лесостепной зоны На этапе...
-
Точка безубыточности (break-even point) это минимальный объем производства и реализации товаров (работ, услуг), при котором расходы будут компенсированы...
-
Средняя арифметическая форма общего индекса Является преобразованием от агрегатной формы. Средняя арифметическая форма общего индекса качественных...
-
Расчет себестоимости товарного выпуска продукции участка цеха за плановый период производится по формуле (10.1): , (10.1) Где Cn. j - полная...
-
Уровень рентабельности единицы продукции ( Ури ) можно принять равным 30-50% от полной себестоимости. Тогда размер нормативной прибыли на единицу...
-
Ориентировочно величина показателя "чистые активы" может быть найдена как разность между собственным капиталом и суммы накопленным убытком (по балансу)....
-
Согласно штатному расписанию ГУП ВО "Облкоммунсервис", на конец 2015 года на предприятии было занято 365 работников. Численность работников в каждом...
-
1) ?К = ЗКап Где ?К - изменение капитальных затрат, руб./год; ЗКап - общая стоимость дополнительных капитальных затрат, руб./год (взять из...
-
Согласно штатному расписанию ГУП ВО "Облкоммунсервис", на конец 2015 года на предприятии было занято 365 работников. Численность работников в каждом...
-
Затратный подход к оценке стоимости предприятия - Методы (подходы) оценки стоимости фирмы (бизнеса)
Оценка бизнес стоимость линия Затратный (имущественный) подход рассматривает стоимость предприятия с точки зрения понесенных издержек на его...
-
Введение - Показатели работы автотранспортного предприятия
Результаты работы парка подвижного состава любой АТО оцениваются системой технико - эксплуатационных показателей (ТЭП), характеризующих количество и...
-
При определении потребности в смазочных материалах необходимо учитывать, что своевременная и качественная смазка агрегатов и деталей значительно удлиняет...
-
Стимулирование торгового персонала розничной торговли с целью увеличения объема продаж вторговой организации ОАО "Магнит" состоит из административных,...
-
Организационно-экономическая характеристика ОАО "Магнит" Компания отсчитывает свою историю с 1994 года, когда ее нынешний владелец Сергей Галицкий...
-
1. Абалонин С. М. "Коммерческая деятельность на автотранспорте": Учеб. пособие. - Саратов: СГТУ, 2011. 2. Бучин Е. Д., Костров В. Н. "Маркетинг на...
Прогнозирование сезонных колебаний объема перевозок - Статистика грузового автотранспортного предприятия