Булево линейное программирование. Решение транспортной задачи с замкнутым маршрутом и возвращением в исходный пункт

Это задача оптимизации, в которой переменные принимают только два значения: "единица - ноль". Пример - задача "коммивояжера".

Цель работы: минимизировать продолжительность замкнутого маршрута при выезде из начального пункта, проезде через все заданные пункты с возвратом в него.

Программное обеспечение: программа линейного математического программирования "LINDO (LINGO".

Условия задачи. Всего 5 пунктов, включая начальный пункт N1. Дана таблица (матрица) времени, затрачиваемого на переезд из каждого пункта (i) в каждый из остальных пунктов (j) - TIj и наоборот (табл.1).

Таблица 1 Таблица времени, затрачиваемого на переезд из одного пункта в другой

Из пункта I	В пункт J
1	2	3	4	5
1 2 3 4 5	0 1 8 14 10	10 0 9 10 8	25 10 0 24 25	25 15 20 0 27	10 2 10 15 0

Для составления математической модели необходимо ввести булевы переменные следующим образом: Принимаем, что

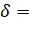
1, если из пункта I едем в пункт J; 0 - в противном случае (обратно).

Из пункта 1 можно выехать в любой из пунктов 2-5 или остаться в пункте 1. Но при этом можно выехать только в одном направлении. Это условие можно записать так:

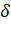
11 + 12 + 13 +14 + 15 = 1 или 1j =1.

Если из пункта i выехать в произвольный J- ый пункт, то запишем:

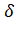
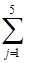
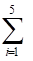
Ij =1, J = 1,...,5.

В результате задачу математически можно записать следующим образом:

XIjij min. - целевая функция.

Ограничения: Ij =1, J = 1,...,5; - выезд из пункта I;

Ij =1, I = 1,...,5; - въезд в пункт J.

Конкретно для представленной таблицы времени целевая функция выглядит так:

F = t1111 + t1212 + t1313 + t1414 + t15 15 + t2121 + t2222 + ... + t5555 min.

Значения t берутся из таблицы, а Ij являются искомыми переменными. Это булевы переменные. Они могут иметь 2 значения: 1 или 0.

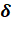
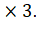
Для простоты демонстрации решения задачи воспользуемся только тремя пунктами: 1, 2 и 3 из табл.1, т. е. рассмотрим матрицу 3 В таком случае целевую функцию можно представить следующим образом:

F = 1012 + 2513 + 121 + 1023 + 831 + 9 32 min

Ограничения:

Из пункта 1: 12 + 13 = 1; в пункт 1: 21 + 31 = 1;

Из пункта 2: 21 + 23 = 1; в пункт 2: 12 + 32 = 1;

Из пункта 3: 31 + 32 = 1; в пункт 3: 13 + 23 = 1.

Граничные условия: Ij >0, Ij <0.

Для программы LINDO (LINGO) дополнительно после END можно обозначить эти величины как целые: GIN 12, 13, GIN 32.

Результаты: 12 =1, 13 =0, 21 =0,23 =1, 31 =1, 32 =0.

Значит, наиболее быстрый маршрут: пункты 1 > 2 > 3 > 1.

Минимальное время: 10 +10 +8 = 28 единиц времени.

Далее представлен листинг программы LINDO (LINGO) для решения представленного примера решения задачи.

Листинг программы.

MIN 1012 + 2513 + 121 + 1023 + 831 + 9 32 - целевая функция

SUBJECT TO

12 + 13 = 1; - ограничения 21 + 31 = 1; 21 + 23 = 1; 12 + 32 = 1; 31 + 32 = 1; 13 + 23 = 1. 12 >0 - граничные условия 12 13 >0 13 21 >0 21 23 >0 23 31 >0 31 32 >0 32

END

GIN 12 - обозначения целых величин

GIN 13

GIN 21

GIN 23

GIN 31

GIN 32

Задание: в соответствии с представленным примером минимизировать замкнутый маршрут по 5 пунктам, т. е. по данным всей матрицы, представленной в табл.1.

Оптимизация функционирования системы при заданных ресурсных ограничениях

Цель работы: оптимизировать систему с ресурсными ограничениями.

Все, что необходимо для производственного процесса (финансы, рабочая сила, сырье и т. п.) можно объединить понятием "ресурсы", среди которых можно выделить три основные группы: трудовые, материальные и финансовые. Большинство задач, возникающих в производстве можно рассматривать как преобразование ресурсов в результат (получение продукта и его реализацию). Поэтому значительная часть задач, возникающих при управлении производством, относится к классу задач распределения ресурсов.

Программное обеспечение: программа линейного математического программирования "LINDO (LINGO".

В настоящей лабораторной рассматриваются два основных варианта задач.

Первый вариант: Максимизировать полученный результат - R (количество продуктов или прибыль) при заданных ресурсах (Q).

Модель оптимизируемой системы:

Модель целевой функции (F):

F=R= J max (прибыль),

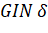
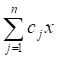
Где: cJ - прибыль, получаемая от единицы j-ой продукции;

XJ - количество продукции j - го вида;

N - количество видов продукции.

Модель ограничений (ресурсов):

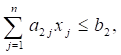
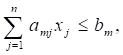
Где: аIj - количество i - го ресурса, необходимого для изготовления еди ницы j - го вида продукции;

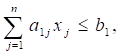
BI - запас i - го ресурса;

M - количество видов ресурсов.

Граничные условия: xJmin ? xJ? xJmax.

Решение первого варианта задачи:

Все исходные данные приведены в табл. 1.

Таблица 1 Исходные данные

Ресурсы	Вид продукции	Располагаемый ресурс
П1	П2	П3	П4
Трудовые	1	2	3	4	40
Материальные	6	5	4	3	110
Финансовые (на единицу продукции)	4	6	8	12	100 Сумма 250
Граница выпуска: Нижняя Верхняя	1 12	0 -	2 -	3 3
План выпуска	X1	X2	X3	X4
Прибыль от единицы продукции	60	70	120	130

Задача: рассчитать такой план выпуска продукции, который обеспечит максимум прибыли при заданных ограничениях (ресурсах).

Листинг программы "LINDO"

MAX 60x1 + 70x2 +120x3 +130x4

SUBJECT TO

X1+2X2+3X3+4X4 <=40

6X1+5X2+4X3+3X4 <= 110 4x1+6x2+8x3+12x4 <= 100

X1>=1

X1<=12

X2>=0

X3>=2

X4=3

END

Результаты:*

1350 - максимальная прибыль

X1 = 12

X2 = 0 > оптимальное количество выпускаемой продукции

X3 = 2

X4 = 4

*На остальные цифры не обращать внимания

Далее необходимо подсчитать затраченные ресурсы (Q) как сумму произведений затраты ресурсов на единицу соответствующей продукции на вычисленное количество выпуска этой продукции: 30 + 89 +100 = 219

Коэффициент эффективности системы: 1350/219=6,16.

Второй вариант:

При заданной прибыли, например, R=1350 минимизировать используемые ресурсы Q.

C этой целью в модель вводятся дополнительные переменные: Y1, Y2, Y3.

Каждая из этих переменных является оценкой соответствующего неиспользуемого ресурса, т. е. разностью между располагаемым и потребленным ресурсом. Эта величина должна быть минимизирована. Следовательно, Модель целевой функции имеет следующий вид:

F = Y1+Y2+Y3 > max

В результате Модель ограничений приобретает следующий вид:

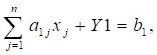
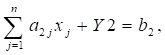
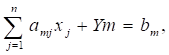
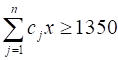
Сюда же добавляется еще одно ограничение по прибыли (R):

Граничные условия сохраняются.

Листинг программы:

MAX Y1+Y2+Y3

SUBJECT TO

X1 + 2X2 + 3X3 + 4X4 + Y1 = 40

6X1 + 5X2 + 4X3 + 3X4 + Y2 =110 4X1 + 6X2 + 8X3 + 12X4 +Y3 =100 60X1 + 70X2 + 120X3 +130X4 >=1350

X1>=1

X1<=12

X2>=0

X3>=2

X4 = 3

END

Результаты:

69,5 (сумма неиспользованного ресурса, т. е. Y1+Y2+Y3)

Y1 = 4,5

Y2 = 65

Y3 = 0

X1 = 1

X2 = 0

X3 = 7,5

X4 = 3

В итоге:

1) прибыль (R) равна 1350 ед. 2) количество используемых ресурсов: Q = 250 - 69,5 = 180,5 3) план выпуска продукции: X1 = 1, X2 = 0, X3 = 7,5, X4 =3 4) коэффициент эффективности k = 1350/180,5 = 7,48.

Таким образом, в результате проведения двухступенчатой оптимизации удалось рассчитать такой план выпуска продукции, который обеспечит получение максимально возможной при заданных ресурсах прибыли при максимально возможной экономии ресурсов.

Задание: в соответствии с представленным примером оптимизировать план выпуска продукции, прибыль от единицы которой составляет 60, 70, 130, 150 для каждого продукта. Остальные параметры системы сохранены без изменений.

Многокритериальная оптимизация. Реализация метода последовательных приближений в задаче с ресурсными ограничениями

Цель работы: решить задачу оптимизации системы с ресурсными ограничениями, имеющую две целевые функции - прибыль от реализации продукции и затраты ресурсов.

Программное обеспечение: программа линейного математического программирования "LINDO (LINGO". Приведен листинг программы.

Исходные условия задачи. Для изготовления двух видов продукции (x1, x2) используются два вида ресурсов (y1, y2). Дано количество ресурсов в условных единицах, затрачиваемых на изготовление единицы продукции:

Таблица 1. Исходные данные для решения задачи оптимизации

Вид ресурса

Запас ресурса

Число единиц ресурсов, затраченное на изготовление единицы продукции

18 16

1 2

3 1

Даны также запасы ресурсов в условных единицах: S1 ? 18, S2 ? 16.

Прибыль получается от единицы продукции (x1,x2) соответственно 2 и 3 денежные единицы.

Необходимо рассчитать такой план выпуска продукции (x1, x2), который обеспечит Максимум прибыли (первая целевая функция) и минимум затраченных ресурсов (вторая целевая функция).

Алгоритм решения поставленной задачи:

1. Построить модель системы. 2. Последовательное нахождение таких значений величин x1 и x2, которые обеспечат минимизацию затрат ресурсов при различных заданных величинах прибыли, например: 900, 950, 1000, 1050, 1100 денежных. ед., пока будет хватать ресурсов. С этой целью целесообразно использовать программу линейного программирования LINDO (LINGO), листинг которой приведен ниже. На каждом этапе расчетов определяется коэффициент эффективности. 3. Все результаты расчетов, выполненные в предыдущем пункте, сводятся в таблицу, на основе которой осуществляется процедура выбор адекватного варианта решения.

Пример решения поставленной задачи.

Первый этап. Моделирование системы.

На рис.1 приведена блок-схема объекта исследования:

Рис.1. Блок-схема объекта исследования.

Функция прибыли: y1= 2x1 + 3x2 .

Функции потребления ресурсов: y2 = x1 +3x2 18,

(модели ограничений ресурсов) y3 = 2x1 + X2 16.

Второй этап. Последовательное проведение минимизации затраченных ресурсов для следующей последовательности зафиксированных значений прибыли: 10, 15, 17 и т. д. денежных единиц до конца имеющихся ресурсов. C этой целью в модель вводятся дополнительные переменные: z2, z3. Каждая из этих переменных является оценкой соответствующего неиспользуемого ресурса, т. е. разностью между располагаемым и потребленным ресурсом. Эта величина должна быть минимизирована. Следовательно, Модель целевой (минимизируемой) функции имеет следующий вид:

F = z2+ z3 > max.

В результате Модели ограничений ресурсов приобретают следующий вид:

Y2 = x1 +3x2 + z2 = 18,

Y3 = 2x1 + X2 + z3 =16.

Сюда добавляется функция ограничения по прибыли (yОгр) :

Y1= 2x1 + 3x2 ? yОгр

Ниже представлен листингпрограммы LINDO, с помощью которой последовательно проводится минимизация затрат при различных заданных значениях прибыли: 10, 15, 17, 22 и 24 ден. ед. Каждый раз вычисляются затраты ресурсов и коэффициент эффективности (Кэф.), равный отношению прибыли к затратам. Результаты сведены в табл.2.

Листинг программы LINDO (LINGO):

MAX Z2+ Z3

SUBJECT TO

X1 + 3X2 + Z2 = 181

2X1 + X2 + Z3 = 16 2X1 + 3X2 >=10 (начальная величина зафиксированной прибыли)

X1>=1 граничные условия

X2>=1

END1

GIN X1 обозначения целых величин

GIN X2

Таблица 2 Результаты экспериментов

Прибыль	10	15	17	22	24
Затраты	14	21	23	33	34
Кэф	0,71	0,71	0,74	0,67	0,70
Выпуск продукции (x1,x2)	2 2	3 3	1 5	5 4	6 4

На основании сравнительного анализа результатов необходимо принять решение о выборе одного из двух вариантов плана выпуска продукции (x1, x2) : при максимальной эффективности производства (третья колонка) или при максимальной прибыли, но не самой высокой эффективности (последняя колонка).

Задание: осуществить оптимизацию представленной системы в соответствии с приведенным примером, но с измененными данными об ограничениях по ресурсам: 20 вместо 18 по одному (y2) и 18 вместо 16 по другому (y3) ресурсу.

Решение транспортной задачи на основе метода линейного программирования

Цель работы: минимизировать суммарные транспортные расходы в соответствии с представленной на рис.1 схемой.

Программное обеспечение: программа линейного программирования LINDO. маршрут ограничение транспортный задача

Необходимо перевезти продукцию от поставщика (склады A1 A2) к потребителю в три точки: B1 B2 B3, как показано на схеме:

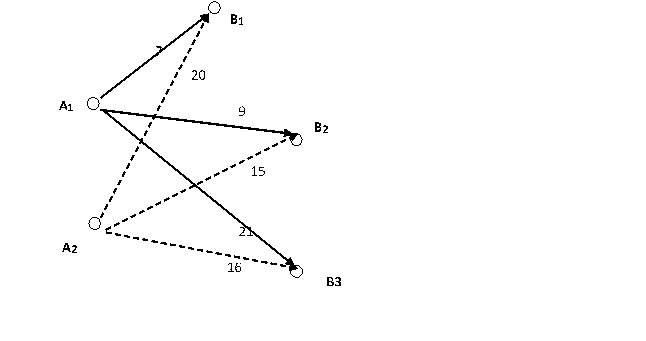
Рис.1. Схема доставки груза. Цифрами отмечены транспортные затраты на перевозку единицы груза

Таблица условий

Поставщик	Потребитель (заказчик)	Запасы
В1	В2	В3
А1	7 X11	9 X12	21 X13	100
А2	20 X21	15 X22	16 X23	200
Заявки	80	130	90	300

Примечания: 1) xIj - число единиц груза, которые i - ый поставщик должен отправить j - му потребителю; 2) в углах ячеек представлены транспортные затраты на перевозку единицы груза в соответствующем направлении.

Задача: минимизировать суммарные транспортные расходы.

Модель системы:

Целевая функция (F):

F = 7x11 +9 x 12 +21 x 13 +20 x 21 +15 x 22 +16 x 23 > min.

Ограничения:

X11 + x12 + x13 = 100,

X21 + x22 + x23 = 200,

X11 + x21 = 80,

X12 + x22 = 130,

X13 + x23 = 90.

Граничные условия: xIj ? 0, где i = 1, 2 ; j = 1, ..., 3.

Решение задачи: листинг программы Lindo (Lingo)

MIN 7x11 +9 x 12 +21 x 13 +20 x 21 +15 x 22 +16 x 23 - целевая функция

SUBJECT TO

X11 + x21 = 80 - ограничения

X12 + x22 = 130

X13 + x23 = 90

X11 + x12 + x13 = 100

X21 + x22 + x23 = 200

X11 >=0 x21 >=0 - граничные условия

X12 >=0 x22 >=0

X13 >=0 x23>=0

END

Результаты: минимальные суммарные транспортные расходы (FMin) составляют 3830 денежных единиц. Такой результат может быть достигнут при перевозке груза в следующих пропорциях:

X11 = 80; x21 = 0;

X12 = 20; x22 = 110;

X13 = 0; x23 = 90;

Задание: рассчитать минимальные транспортные расходы и оптимизировать перевозку груза в соответствии со схемой, представленной на рис.2.

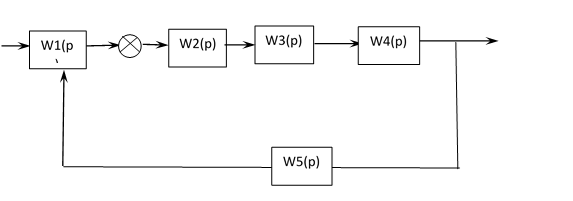
Рис.2. Схема доставки груза для выполнения лабораторной работы

Булево линейное программирование. Решение транспортной задачи с замкнутым маршрутом и возвращением в исходный пункт

Похожие статьи