Постановка задачи, Случаи вырождения и способы их преодоления - Транспортная задача линейного проектирования
Цель работы.
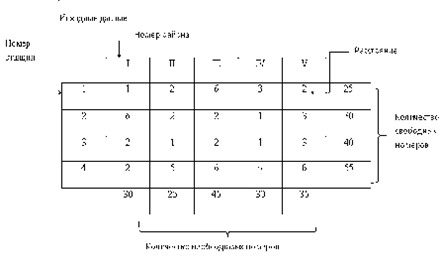
В городе имеется четыре АТС со свободной номерной емкостью (1,2,3,4). Известно количество свободных телефонных номеров на каждой станции. Также имеется пять районов (1,2,3,4,5), которые требуют телефонизации. Известно также расстояние от каждой АТС до центра каждого района. Нужно разделить имеющуюся телефонную емкость между районами так, чтобы расход кабеля и стоимость всей операции были минимальными. (Номера от одной АТС могут попадать в разные районы).
Определение транспортной задачи.
Такого рода задачи решаются с помощью алгоритма, который называется транспортной задачей линейного программирования. Существуют два типа транспортной задачи: открытая и закрытая. Транспортная задача называется открытой, если сумма запасов отличается от суммы заявок. Транспортная задача называется закрытой, если сумма запасов равняется сумме заявок. Решение существует только для закрытой транспортной задачи, поэтому, если транспортная задача открытая, то ее надо привести к закрытому типу. Для этого в случае, если количество запасов превышает количество заявок, вводят фиктивного потребителя, который выбирает весь избыток запасов. В случае же, если заявок больше, чем запасов, то вводят фиктивного поставщика, с фиктивным количеством запасов. В обоих случаях в матрице тарифов перевозок данному складу или потребителю проставляется нулевая цена перевозок.
Подсчитаем суммы номерных емкостей: количество необходимых номеров: 30+25+45+30+35=165; количество свободных номеров: 25+30+40+55=150. Т. к. в нашем случае число заявок превышает количество свободных номеров, то задача является открытой. Значит, какие-то районы недополучат требуемых телефонных номеров. Чтобы сбалансировать задачу, необходимо ввести фиктивную строку с нулевыми расстояниями. Тогда задачу можно представить в виде матрицы следующего вида: сверху в строку пишем районы, которые нуждаются в телефонизации, в первый столбец пишем станции 1,2,3,4,5, в нижней строке и соответствующем столбце пишем потребность районов в телефонных номерах. В последнем столбце пишем свободную номерную емкость. Матрица имеет вид:
Таблица 1
|
Телефонные станции |
Районы |
Свободные номера | ||||
|
I |
II |
III |
IV |
V | ||
|
1 |
1 |
2 |
6 |
3 |
2 |
25 |
|
2 |
6 |
2 |
2 |
1 |
3 |
30 |
|
3 |
2 |
1 |
2 |
1 |
3 |
40 |
|
4 |
2 |
5 |
6 |
4 |
6 |
55 |
|
5 |
0 |
0 |
0 |
0 |
0 | |
|
Заявки |
30 |
25 |
45 |
30 |
35 |
Целью решения задачи является отыскание такого распределения ресурсов по работам, при котором либо минимизируются общие затраты, связанные с выполнением работ, либо максимизируется получаемый в результате общий доход.
Поставим эту задачу как задачу линейного программирования. Обозначим xij - количество номеров, отдаваемых i-й телефонной станцией j-району. Неотрицательные переменные xij тоже можно записать в виде матрицы:
X11 x12 ...x1n
X21 x22 ...x2n (1)
................
Xm1 xm2 ...xmn,
Которая коротко обозначается (xij). Совокупность чисел (xij) называется "планом перевозок", а сами величины xij - "перевозками". Эти неотрицательные переменные должны удовлетворять следующим условиям:
1. Суммарное количество номеров, отдаваемых каждой АТС во все районы, должно равняться количеству свободных номеров в данной АТС. Это даст нам m условий-равенств:
X11+x12+...+x1n=a1,
X21+x22+...+x2n=a2, (2)
.......................
Xm1+xm2+...+xmn=am.
2. Суммарное количество номеров, отдаваемых в каждый район от всех АТС, должно быть равно заявке, поданной данным районом. Это даст нам n условий-равенств:
X11+x12+...+x1n=b1,
X21+x22+...+x2n=b2, (3)
.......................
Xm1+xm2+...+xmn=bm.
3. суммарная стоимость всех операций, т. е. сумма величин xij, умноженных на соответствующие стоимости сij, должна быть минимальной:
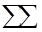
S=cijxij=min, (4)
I=1 j=1
Где знак двойной суммы означает, что суммирование производится по всем комбинациям индексов i и j.
У нас задача линейного программирования с условиями-равенствами (2), (3) и минимизируемой линейной функцией (4). Все коэффициенты в условиях (2), (3) равны единице. Условия-равенства (2), (3) не являются линейно-независимыми. Число линейно-независимых среди уравнений (2), (3) равно m+n-1. Общее число переменных xij в нашей задаче равно m*n, число базисных переменных будет равно m+n-1, а число свободных переменных k=m*n-(m+n-1)=(m-1)*(n-1).
Любой план перевозок называется допустимым, если он удовлетворяет условиям (2), (3) (все заявки удовлетворены, все запасы исчерпаны). Допустимый план будет называться опорным, если в нем отличны от нуля не более m+n-1 базисных перевозок, а остальные перевозки равны нулю. План будет называться оптимальным, если он, среди всех допустимых планов, приводит к минимальной суммарной стоимости перевозок.
Случаи вырождения и способы их преодоления
Выше отмечалось, что число занятых мест в таблице должно быть равно m+n-1. Однако на практике встречаются случаи, когда в процессе решения оно сокращается.
Это явление называется вырождением. Для преодоления этого в одну из освободившихся клеток ставится 0 и эта клетка считается занятой. Иногда приходится встречаться с вырождением уже при составлении исходного решения. Вырождения в этом случае можно избежать, переставляя местами столбцы и строки.
Похожие статьи
-
Транспортная задача (Т. З.) является одной из распространенных задач линейного программирования специального вида. Эта задача такого наиболее...
-
Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования,...
-
Введение - Транспортная задача линейного проектирования
В настоящее время оптимизация находит применение в науке, технике и в любой другой области человеческой деятельности. Оптимизация - целенаправленная...
-
Транспортная задача - Линейное программирование
Одна из наиболее распространенных задач математического программирования -- транспортная задача. В общем виде ее можно представить так: требуется найти...
-
Разработать и создать аналог системной утилиты "Диспетчер задач" по дисциплине "Системное программирование". "Диспетчер задач" должен содержать следующие...
-
Теорема. Чтобы транспортная задача была разрешима, необходимо и достаточно, чтобы выполнялось условие: (1.5) Доказательство: Необходимость. Пусть...
-
Постановка задач на проектирование Мотивация: В настоящее время есть возможность улучшить эффективность управлением временем и коммуникацией между...
-
Транспортная задача оптимальность Поставим в соответствие поставщикам потенциалы Ui, , а потребителям - Vj, . В оптимальном плане для всех базисных...
-
Признак оптимальности плана перевозок T. З. устанавливает теорема. Теорема. Для того, чтобы некоторый допустимый план X = (xij)m-nT. З. был оптимальным,...
-
Анализ предметной области Описание ПО решаемой задачи Предметной областью задачи № 2 также является процесс оплаты денежных средств по кредиту. Решается...
-
Задача Разработать автоматизированное рабочее место медицинского работника дошкольного учреждения. Постановка задачи Информация о функционировании...
-
Методы разработки вычислительной сети: 1. Экспериментальный метод - персонал предприятия закупает "новинки" рынка компьютерной техники. Такой метод -...
-
Формулировка задачи - Линейное программирование
Даны линейная функция Z=С1 х1 +С2 х2 +...+СN xN (1.1) И система линейных ограничений A11 x1 + a22 x2 +... + a1N ХN = b1 A21 x1 + a22 x2 +... + a2N ХN =...
-
Методика решения задач ЛП графическим методом - Линейное программирование
I. В ограничениях задачи (1.2) заменить знаки неравенств знаками точных равенств и построить соответствующие прямые. II. Найти и заштриховать...
-
Анализ предметной области Предметной областью задачи является процесс определения суммы налога на дарение. Известны сумма подарков в МРОТ (минимальный...
-
Специфика транспортной задачи позволяет находить новое опорное решение задачи и новый базис по правилу более простому, чем в симплекс-методе. Пусть...
-
Пересчет симплекс-таблицы. - Транспортная задача
Формируем следующую часть симплексной таблицы. Вместо переменной x в план 1 войдет переменная x1 . Строка, соответствующая переменной x1 в плане 1,...
-
Вычислить максимум функции F(x)=-L(x1)x2+3.1L(x2)x+5 на отрезке [a;b] с точностью е. L(x1), L(x2) - значения интерполяционного многочлена, построенного...
-
"РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ MICROSOFT EXCEL" Цель работы Приобретение навыков решения задач линейного программирования...
-
Целью дипломного проекта "Калькулятор коммунальных услуг" является разработка программного средства "Calculation. exe". Для достижения цели дипломного...
-
Постановка задачи Основная задача автоматизации документооборота в работе состоит в оптимизации бизнес-процесса на уровне обработки документов...
-
В настоящей главе будет произведен разбор частного случая задачи оптимальной фильтрации. На примере будет разобран ход построения алгоритма, будут...
-
Организационно-экономическая сущность задачи Основные организационно - экономические показатели: сокращение времени разработки документации предприятия...
-
Целью данного курсового проекта является разработка и описание работы устройства управления, вырабатывающего заданную по варианту последовательность...
-
Метод конечных элементов (МКЭ) жесткости возник в аэрокосмической отрасли. Исследователи рассматривали различные подходы к анализу сложных частей...
-
Оргтехника, ПК, телефонные аппараты На данный момент начальник ДЧ ЛОП использует комплекс технических средств, который предназначен для обработки...
-
Задачи и функции линейного отдела полиции Отдел возглавляет начальник, назначаемый на должность и освобождаемый от должности в установленном порядке....
-
Практическая часть, Постановка задачи, Инструмент рендеринга - Моделирование эффектов
Постановка задачи В качестве практической задачи необходимо разработать следующий алгоритм. Вход: - фотография, в которую будет вставлен синтетический...
-
Необходимо исследовать зависимость влияния различных факторов на параметр, характеризующий производство. В качестве такого параметра было выбрано...
-
Построение модели предметной области с помощью описания структур данных и программного кода является классическим подходом в разработке ИС. Зачастую...
-
В клубе несколько команд (дети, юноши, дубль, основа). Каждая команда имеет своего тренера и базу. В каждой команде есть несколько футболистов разных...
-
На рисунке 1 представлен фрагмент электронной таблицы, в которой содержаться исходные данные для решения задачи. Рисунок 1 - Фрагмент электронной...
-
Постановка задачи На стадии оперативного управления возможна замена материалов и комплектующих, указанных в спецификациях, их аналогами. Аналогами...
-
1.2.1 Уточнение постановки задачи Для анализа в рамках проекта выберем очень простые, но от этого не менее актуальные , задачи БД отеля. 1. Добавление...
-
Постановка задачи Назначением сайта является помощь пользователям интернета в короткие сроки находить ответ на интересующий вопрос. Пользователи,...
-
Постановка задачи - Расчет трудоемкости средствами Ms Excel
Необходимо рассчитать нормативную трудоемкость квартальной и месячной производственной программы цеха по деталям. Для этого необходимо перемножить...
-
Аннотация В статье рассматриваются два способа уменьшения времени вычисления дерева решений для задач линейного параметрического программирования с...
-
Постановка задачи Имеющаяся база данных SQL имеет недостаточное количество полей и таблиц, не имеет упорядоченной структуры пользователей для работы с...
-
Постановка задачи Основной целью дипломной работы является создание комплексной системы информационной безопасности предприятия на примере информационной...
-
Аналитический способ решения задачи №3 представляет собой проверку вычислений: - для лица Лушников В. В. сумма налога на дарение составит 0, т. к. сумма...
Постановка задачи, Случаи вырождения и способы их преодоления - Транспортная задача линейного проектирования