Модель управления обучением - Методология моделирования процессов управления в социально-экономических системах
В качестве примера конкретной модели процесса управления обсудим модель распределения времени между овладением знаниями и развитием умений, впервые кратко рассмотренную в [26]. При моделировании исходим из того, что любое знание состоит частично из "информации" ("чистое знание") и частично из "умения" ("знаю как"). Умение - это мастерство, это способность использовать имеющиеся у вас сведения для достижения своих целей; умение можно еще охарактеризовать как совокупность определенных навыков, в конечном счете, умение - это способность методически работать [27, с.308].
Пусть X(T) - объем сведений, накопленных учащимся к моменту времени T ("чистое знание"), Y(T) - объем накопленных умений: умений рассуждать, решать задачи, разбираться в излагаемом преподавателем материале; U(T) - доля времени, отведенного на накопление знаний в промежутке времени (T; t + Dt).
Примем в модели в качестве исходного положения, что увеличение X(T + Dt) - X(T) объема знаний учащегося пропорционально потраченному на это времени U(T)Dt и накопленным умениям Y(T). Следовательно,
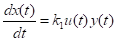
, (1)
Где коэффициент k1 > 0 зависит от индивидуальных особенностей учащегося.
Примем также, что увеличение знаний за то же время пропорционально потраченному на это времени (1 - U(T))Dt, имеющимся умениям Y(T) и знаниям X(T). Следовательно,
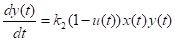
. (2)
Коэффициент K2 > 0 также зависит от индивидуальности. Учащийся тем быстрее приобретает умения, чем больше он уже знает и умеет. Тем быстрее усваивает знания, чем больше умеет. Но нельзя считать, что чем больше они запомнил, тем быстрее запоминает. На правую часть уравнения (1) влияют только приобретенные в прошлом активные знания, примененные при решении задач и перешедшие в умения. Отметим, что модель (1) - (2) имеет смысл применять на таких интервалах времени, чтобы, например, пять минут можно было считать бесконечно малой величиной.
Можно управлять процессом обучения, выбирая при каждом T значение функции U(T) из отрезка [0; 1]. Рассмотрим две задачи.
- 1. Как возможно быстрее достигнуть заданного уровня знаний X1 и умений Y1? Другими словами, как за кратчайшее время перейти из точки фазовой плоскости (X0; Y0) в точку (X1; Y1)? 2. Как быстрее достичь заданного объема знаний, т. е. выйти на прямую X = X1?
Двойственная задача: за заданное время достигнуть как можно большего объема знаний. Оптимальные траектории движения для второй задачи и двойственной к ней совпадают (двойственность понимается в обычном для математического программирования смысле [28]).
С помощью замены переменных Z = K2X, W = K1K2Y перейдем от системы (1) - (2) к более простой системе дифференциальных уравнений, не содержащей неизвестных коэффициентов:
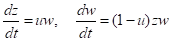
. (3)
(Описанная линейная замена переменных эквивалентна переходу к другим единицам измерения знаний и умений, своим для каждого учащегося.)
Решения задач 1 и 2, т. е. наилучший вид управления u(t), находятся с помощью математических методов оптимального управления, а именно, с помощью принципа максимума Л. С. Понтрягина [29]. В задаче 1 для системы (3) из этого принципа следует, что быстрейшее движение может происходить либо по горизонтальным (U = 1) и вертикальным (U = 0) прямым, либо по особому решению - параболе W = Z2 (U = 1/3). При движение начинается по вертикальной прямой, при - по горизонтальной, при - по параболе. По каждой из областей {Z2 > W} и {Z2 < W} проходит не более одного вертикального и одного горизонтального отрезка оптимальной траектории.
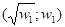
Используя теорему о регулярном синтезе [29, с.266], можно показать, что оптимальная траектория выглядит следующим образом. Сначала надо выйти на "магистраль" - добраться до параболы W = Z2 по вертикальной (U = 0) или горизонтальной (U = 1) прямой. Затем пройти основную часть пути по магистрали (U = 1/3). Если конечная точка лежит под параболой, добраться до нее по горизонтали, сойдя с магистрали. Если она лежит над параболой, заключительный участок траектории является вертикальным отрезком. В частности, в случае оптимальная траектория такова. Сначала надо выйти на магистраль - добраться по вертикальной (U = 0) прямой до параболы. Затем двигаться по магистрали (U = 1/3) от точки до точки. Наконец, по горизонтали (U = 1) выйти в конечную точку.
В задаче 2 из семейства оптимальных траекторий, ведущих из начальной точки (Z0; W0) в точки луча (Z1; W1), W0 < W1 < +?, выбирается траектория, требующая минимального времени. При Z1 < 2Z0 оптимально W1 = Z0 (Z1 - Z0), траектория состоит из вертикального и горизонтального отрезков. При Z1 > 2Z0 оптимально, траектория проходит по магистрали W = Z2 от точки до точки. Чем большим объемом знаний Z1 надо овладеть, тем большую долю времени надо двигаться по магистрали, отдавая при этом 2/3 времени увеличению умений и 1/3 времени - накоплению знаний.
Полученное для основного участка траектории оптимального обучения значение U = 1/3 можно интерпретировать приблизительно так: на одну лекцию должно приходиться два семинара, на 15 мин. объяснения 30 мин. решения задач. Результаты, полученные в математической модели, вполне соответствуют эмпирическим представлениям об оптимальной организации учебного процесса. Кроме того, модель определяет численные значения доли времени (1/3), идущей на повышение знаний, и доли материала (1/2), излагаемого на заключительных лекциях (без проработки на семинарах).
При движении по магистрали, т. е. в течение основного периода учебного процесса, оптимальное распределение времени между объяснениями и решением задач одно и то же для всех учащихся, независимо от индивидуальных коэффициентов K1 и K2. Этот факт устойчивости оптимального решения показывает возможность организации обучения, оптимального одновременно для всех учащихся. При этом время движения до выхода на магистраль зависит, естественно, от начального положения (X0; Y0) и индивидуальных коэффициентов K1 и K2.
Таким образом, модель процесса управления обучением (1) - (2) позволила получить ряд практически полезных рекомендаций, в том числе выраженных в числовой форме. При этом не понадобилось уточнять способы измерения объемов знаний и умений, имеющихся у учащегося. Достаточно было согласиться с тем, что эти величины удовлетворяют качественным соотношениям, приводящим к уравнениям (1) и (2).
Многочисленные модели процессов управления описаны в литературе [2, 14, 17, 18, 21, 24, 16]. Их практическим использованием обычно занимаются информационно-аналитические подразделения, службы контроллинга, качества и надежности, маркетинга и др. К тематике настоявшей статьи непосредственное отношение имеют работы А. М. Новикова и Д. А. Новикова по методологии [30] и Д. А. Новикова по методологии управления [31].
Похожие статьи
-
Модель в общем смысле (обобщенная модель) есть создаваемый с целью получения и (или) хранения информации специфический объект (в форме мысленного образа,...
-
Программное управление является приемлемым подходом во многих прикладных ситуациях. На этом принципе основаны, например, простые металлорежущие станки...
-
Моделирование процессов управления предполагает последовательное осуществление трех этапов исследования. Первый - от исходной практической проблемы до...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
СПОСОБЫ ОПИСАНИЯ СТРУКТУР. МОРФОЛОГИЯ СОЦИАЛЬНО-ПОЛИТИЧЕСКОЙ И ЭКОНОМИЧЕСКОЙ СФЕР Структурное моделирование. Структурный анализ Основная цель...
-
Программное управление Относительно просто может быть сформулирована так называемая задача программного управления. В ней предполагается, что управляющие...
-
Математическое моделирование экономических явлений и процессов с целью оптимизации процессов управления - область научно-практической деятельности,...
-
Обычно субъект экономической жизни стремится достичь сразу многих целей. Например, он стремится одновременно следовать и внутренним, и внешним целям, тем...
-
МЕТОДЫ ОПИСАНИЯ СОЦИАЛЬНО-ПОЛИТИЧЕСКИХ И ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ Динамический образ системы. Системный процесс В своей повседневной жизни процессами люди...
-
Конкретные модели процессов управления в социальных и экономических системах исходят из общей методологии, которую и формулируем в настоящей статье....
-
Принципы оптимальности в изучении социально-экономических процессов рынка труда
Принципы оптимальности в изучении социально-экономических процессов рынка труда Муравьева Мария Петровна С точки зрения системного анализа рынок труда...
-
Рассмотрим две проблемы сравнительной оценки эффективности различных подходов к оптимизации управления экономическими системами. Сравнение по...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Теоретическое обоснование математического моделирования - Математические методы и модели в экономике
Коммерческая деятельность в том или ином виде сводится к решению таких задач: как распорядиться имеющимися ресурсами для достижения наибольшей выгоды или...
-
В большинстве случаев структурная неопределенность вызвана неполнотой знания аналитической структуры уравнений модели объекта управления. При не...
-
Построение, или моделирование, конечной факторной системы для анализируемого экономического показателя хозяйственной деятельности можно осуществить как...
-
Необходимо составить математическое описание теплообменника, в котором жидкий продукт нагревается насыщенным водяным паром (расход, кг/с), до температуры...
-
При управлении подвижными объектами (такими, например, как мобильные роботы, подводные аппараты и т. п.) часто имеет место неопределенность цели, когда...
-
Экономико-математические методы представляют собой совокупность математических методов (математического программирования, теории вероятностей, теории...
-
Модели теории игр. Основные определения и термины В разных областях целенаправленной деятельности, например при разработке и эксплуатации АСУ, часто...
-
Литература - Методология моделирования процессов управления в социально-экономических системах
1. Орлов А. И. Проблемы управления экологической безопасностью. Итоги двадцати лет научных исследований и преподавания. - Saarbrьcken: Palmarium Academic...
-
Модели и моделирование - Экономико-математические методы
Одним из основных методов научного познания является эксперимент, а самой распространенной его разновидностью - метод моделирования систем. В процессе...
-
Календарный производственный программирование однооперационный Все существующие методы решения задач календарного планирования3 по степени достижения...
-
Детерминированные модели, Модель Уилсона - Экономико-математические модели управления запасами
Чрезвычайно трудно построить обобщенную модель управления запасами, которая учитывала бы все разновидности условий, наблюдаемых в реальных системах. Но...
-
Как известно, человечество в своем стремительном развитии старается все более расширить сферы своей деятельности, сталкиваясь при этом с множеством новых...
-
Модели и моделирование. Классификация моделей - Моделирование экономических систем
Первоначально моделью называли некое вспомогательное средство, объект, который в определенных ситуациях заменял другой объект. Например, манекен в...
-
Пусть { , , ..., } - множество возможных состояний некоторой физической системы. В любой момент времени система может находиться только в одном...
-
На основании проведенного моделирования можно сделать выводы: - происходящие тепловые процессы скоротечны и не приводят к перегреву конструкции блока...
-
Моделирование в условиях противодействия, игровые модели - Основы теории систем и системного анализа
Как уже неоднократно отмечалось, системный анализ невозможен без учета взаимодействий данной системы с внешней средой. Ранее упоминалась необходимость...
-
Совершенствование системы управления - сложный и непрерывный процесс воздействия, направленный на более целесообразную организацию управляющей системы...
-
Основные направления совершенствования организационной структуры предприятия ОАО "Огонек". Любую перестройку структуры управления необходимо оценивать, в...
-
Организационная характеристика ОАО "Огонек". ОАО "Огонек" является юридическим лицом. Оно имеет самостоятельный баланс, расчетный счет в банке, печать со...
-
Наиболее ранним способом формализации экономико-математических и ТС является представление физических явлений с помощью систем дифференциальных...
-
Формирование цен различных товаров зависит от большого числа факторов, совокупное влияние которых не может быть детерминировано в рамках общей модели без...
-
Завод по изготовлению телевизоров, находясь в состоянии 1, может увеличить спрос путем организации рекламы. Это требует добавочных затрат и уменьшает...
-
Цепи Маркова служат хорошим введением в теорию случайных процессов, т. е. теорию простых последовательностей семейств случайных величин, обычно зависящих...
-
Функционирование СЭС предусматривает соблюдение четких требований к направлениям ее деятельности. Требуется разработать математический аппарат оценки...
-
Основные понятия и обозначения Динамическое программирование как самостоятельная дисциплина сформировалась в пятидесятых годах двадцатого века. Большой...
-
Введение - Модели оптимального плана управления запасами
Экономико-математической теории управления запасами в 2015 г. исполняется 100 лет (отсчитывая с работы Ф. Харриса [1]). Она входит в логистику - одну из...
-
Этапы моделирования - Общая схема и этапы процесса экономико-математического моделирования
Проанализируем последовательность и содержание этапов одного цикла экономико-математического моделирования. 1. Постановка экономической проблемы и ее...
Модель управления обучением - Методология моделирования процессов управления в социально-экономических системах