Анализ алгоритмов построения сеток - Программное обеспечение расчета конструкций
Общая последовательность построения состоит в следующем. В начале с помощью CAD-системы создается геометрическая 2D-модель исследуемой конструкции. Для этого на данном этапе можно использовать "средние" системы типа AutoCAD, SolidWorks, КОМПАС-3D и др., оснащенные вполне развитым аппаратом двухмерного параметрического моделирования. В отдельных случаях исходную геометрическую модель необходимо перестроить в модель, удобную для построения конечно элементной сетки с учетом особенностей термомеханического нагружения. Затем, уже адаптированная геометрическая модель разбивается на конечные элементы.
В простейшем случае разбивку на четырехузловые конечные элементы можно выполнить, поступив следующим образом. Исследуемая конструкция с помощью пакета AutoCAD "вручную" разбивается на достаточно крупные геометрические примитивы, которые в плане можно рассматривать как 8- и 6-узловые квадратичные конечные элементы, а затем эти геометрические примитивы уже в автоматическом режиме разбиваются на конечные элементы. После этого выполняется процедура автоматической сшивки конечно элементных моделей выделенных геометрических примитивов.
В тех случаях, когда по ходу проведения расчета необходимо перестраивать сетку, например, при исследовании кинетики напряженно-деформированного состояния в процессе обработки материала давлением, всякие "ручные" процедуры, за исключением этапа подготовки начальной геометрии, должны быть исключены. В рамках данной работы предлагается алгоритм, позволяющий автоматически строить конечноэлементные модели, состоящие в основном из четырехузловых конечных элементов и некоторого весьма ограниченного количества трехузловых конечных элементов. Алгоритм реализуется в два этапа: на первом - триангулируется область анализа, а на втором - треугольная сетка перестраивается в четырехугольную.
Начальной информацией является информация о контуре области. Контур области задается в виде линий, каждая из которых рассматривается как одномерный квадратичный конечный элемент (Рис.10а). Нумеруются начальный, конечный и некоторый средний узел каждой линии. В соответствии с конечно элементной технологией в пределах каждой контурной линии узлы имеют локальную нумерацию, а в пределах всего контура те же узлы имеют глобальную нумерацию (таблица 1, Рис.10б). Кроме того, каждому узлу в описании контура ставятся в соответствие координаты и размер шага сетки (таблица 2). Для контура, изображенного на Рис. 10б. .
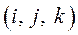
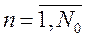
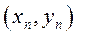
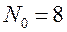
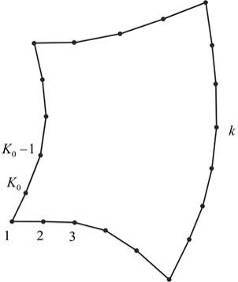
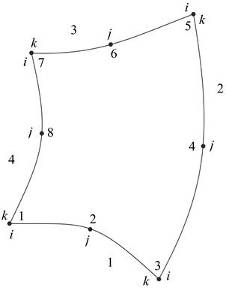
А) б)
Рис. 10. Начальное описание контура и его разбивка
Таблица 1. Описание контурных линий (в соответствии с Рис. 11)
|
Номер Контурной линии |
Локальные узлы | ||
|
1 |
1 |
2 |
3 |
|
2 |
3 |
4 |
5 |
|
3 |
5 |
6 |
7 |
|
4 |
7 |
8 |
1 |
Таблица 2. Описание узлов контурных линий.
|
Номер узла |
|
1 |
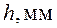
2 |
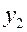
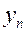
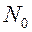
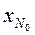
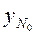
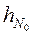
Далее, все контурные линии последовательно разбиваются на отрезки прямых с учетом размеров заданных шагов. Таким образом, формируется массив контурных узлов исходной области
(Рис.10а).
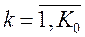
Далее выполняется триангуляция области. Алгоритм триангуляции состоит в следующем. Рассматривается текущий контур, на котором размещены контурные узлы. На первом шаге текущий контур, естественно, совпадает с исходным контуром, который ограничивает триангулируемую область. На контуре определяются три последовательных узла, например, , и, имеющие минимальный угол между построенными на них векторами и (Рис.11). Далее, анализируется геометрическое расположение оставшихся контурных узлов относительно трех выделенных узлов. При этом устанавливается: попадает ли рассматриваемый контурный узел, например, в сектор анализа, характеризуемый величиной угла, и если да, то вычисляются расстояния между узлами, и : и. Если хотя бы одно из этих расстояний меньше максимальной длины векторов и, то проверяются две возможности построения треугольников, показанные на Рис.12. Выбирается та, которая обеспечивает минимум максимального угла в треугольниках. Кроме того, проверяется пересекаемость ребрами треугольников контура. Если построение проходит, то текущий контур разбивается на два подконтура, а затем каждый анализируется отдельно.
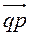
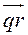
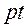
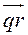
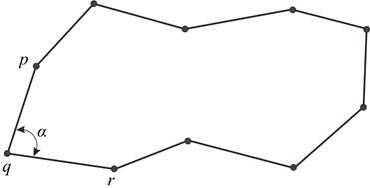
Рис.11. Поиск минимального угла.
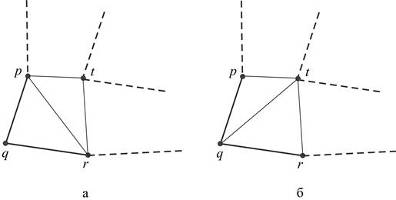
Рис.12. Построение элементов: случай, когда на контуре найден узел.
В том случае, когда не находится узла, который попадал бы в сектор, характеризуемый величиной угла, или расстояния, соединяющие узлы, больше максимальной длины векторов и, то выполняется построение на основе выделенных узлов, и. В зависимости от величины угла возможны два варианта построения, если угол, то треугольник строится на выделенных узлах, , и узел из описания контура исключается (Рис.13а). В противном случае, когда определяется новый узел путем деления угла пополам и строятся два треугольника (Рис 13б), при этом проверяется пересекаемость ребрами треугольников контура. Если построение не проходит, то узел размещается на середине отрезка. Далее узел вводится в описание текущего контура, а узел во всех случаях из описания контура исключается.
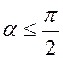
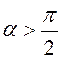
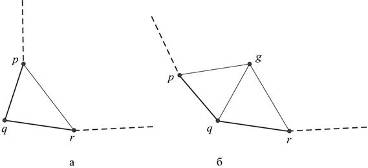
Рис.13. Построение элементов.
После построения конечно элементной модели выполняется ее оптимизация. Оптимизация состоит в коррекции координат внутренних узлов, то есть тех узлов, которые были построены внутри триангулируемых подобластей. Координаты узлов, расположенных на исходном контуре, не изменяются. Оптимизация координат внутренних узлов выполняется следующим образом. Определяются номера конечных элементов, в состав узлов которых входит данный узел, и их число, то есть, фактически определяются все конечные элементы, которые окружают данный узел. Затем, вычисляются координаты центров тяжести всех найденных конечных элементов. В качестве новых координат узла принимаются координаты, вычисленные как среднее арифметическое координат центров тяжести конечных элементов, в состав узлов которых входит данный узел. Эта процедура выполняется несколько раз. Как показывают исследования, для оптимизации необходимо выполнить 5 - 7 итераций. Кроме того, при оптимизации необходимо оценивать соотношение длин сторон треугольников. Если максимальное отношение длин сторон треугольника превышает некоторую заданную величину(обычно ), то наибольшая по длине сторона треугольника делится пополам и соседние треугольники разбиваются на два.
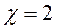
Построение треугольной сетки и ее оптимизация завершают первый этап. На втором этапе треугольная сетка перестраивается в четырехугольную. Перестроение реализуется следующим образом. Последовательно рассматриваются треугольники исходной сетки и их соседи, которые с данным треугольником имеют общие стороны. В качестве примера на Рис. 14. показан рассматриваемый треугольник, имеющий узлы, , и три соседних треугольника, и. Четырехузловой конечный элемент можно построить, объединяя треугольник, например, с треугольником или или. Выбирается комбинация, у которой минимален максимальный угол в четырехугольнике. Треугольники, формирующие четырехугольник из дальнейшего геометрического анализа исключаются.
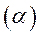
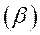
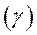
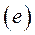
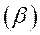
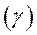
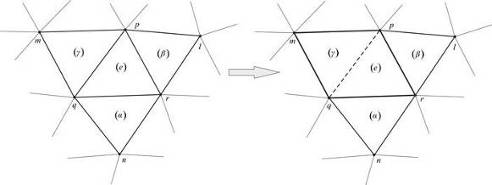
Рис.14. Перестроение сетки.
После процедуры перестроения треугольной сетки в четырехугольную, состоящей в объединении выбранных пар треугольников, может остаться некоторое количество треугольников, которые не удалось объединить. Как показывают исследования, количество треугольных конечных элементов составляет не более 5 - 7 % от общего числа конечных элементов, формирующих конечно элементную модель, и не оказывает заметного влияния на результаты численных исследований.
Второй этап построения сетки также завершается итерационной процедурой коррекции координат внутренних узлов. Определяются номера всех конечных элементов, в состав узлов которых входит рассматриваемый узел, и их общее число. Затем, вычисляются координаты центров тяжести всех найденных конечных элементов. В качестве новых координат узла принимаются координаты, вычисленные как среднее арифметическое координат центров тяжести конечных элементов, содержащих данный узел. Эта процедура выполняется несколько раз. Как показывают исследования, для оптимизации необходимо выполнить 3 - 5 итераций.
Если процесс решения прикладной задачи предусматривает перестроение конечно элементной модели после нескольких этапов нагружения, то геометрической основой построения новой сетки являются узлы тех конечных элементов, стороны которых образуют внешний контур области.
Изложенный алгоритм был реализован в виде комплекса прикладных программ "SETKA-4N-2D". На рисунках 15 и 16 показаны увеличенные фрагменты конечно элементных моделей, построенных с помощью данного комплекса. В канонических областях сетки имеют выраженный структурированный характер, а в областях с криволинейной границей сетки отличаются некоторой нерегулярностью.
Таким образом, разработанный алгоритм позволяет строить сетки в геометрически сложных двухмерных областях и может быть использован при создании алгоритмов для построения сеток в трехмерных областях.
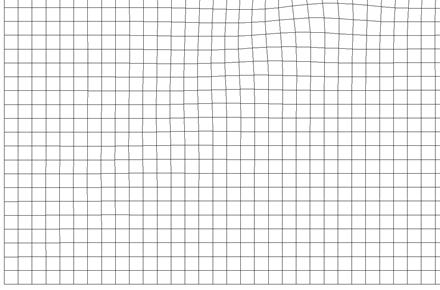
Рис.15. Сетка в канонической области.
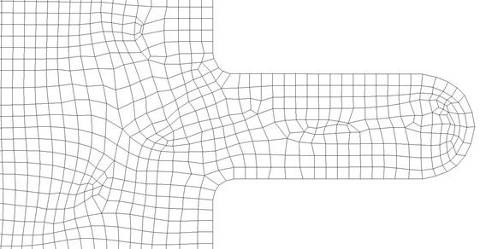
Рис.16. Сетка в области с криволинейной границей.
Многие инженерные задачи и научные исследования требуют решения сложных дифференциальных уравнений с частными производными для трехмерных объектов. В таких случаях обычно используются численные методы математического моделирования, требующие дискретизации исследуемых объектов. Если объектов несколько и форма их сложная, чаще всего применяется метод конечных элементов (МКЭ). В данном методе трехмерные объекты делятся на малые выпуклые многоугольники с фиксированным числом граней, называемые конечными элементами. На практике генерация трехмерной конечно элементной сетки является фундаментальной геометрической проблемой в применении МКЭ [1].
С проблемой генерации сетки тесно связана и проблема ввода и хранения геометрической формы, исследуемых объектов, а во многих случаях еще и вывода результатов в графической форме. Естественным выбором сегодня является какая-либо САПР, которая могла бы взять на себя полное или частичное решение этих задач. Современный рынок программных продуктов предоставляет большое количество разнообразных по возможностям САПР [2]. Большинство из них, малые и средние САПР, обеспечивают только ввод-вывод и хранение геометрической и графической информации. В то же время предлагается и несколько "тяжелых" САПР (ANSYS™, и др.) и несколько специализированных САПР (NASTRAN™, ABAQUS™ и др.), обладающих большими возможностями. Они позволяют выполнить три перечисленные задачи и, кроме того, провести численное моделирование в определенных рамках с помощью того же МКЭ. Большие возможности этих программных пакетов имеют высокую стоимость, требуют мощную вычислительную технику и затраты на обучение. Проведенный анализ показывает, что большинство исследователей предпочитают разрабатывать собственные программы для решения своих задач.
Разрабатывать программу ввода и хранения геометрической формы трехмерных объектов слишком сложно, да и нет необходимости. Проще и эффективней использовать готовую САПР. Поэтому данные задачи были возложены на AutoCAD.
Область исследования и разработки алгоритмов генерации, двухмерных и трехмерных сеток является сегодня одной из самых динамичных и востребованных в численных методах математического моделирования. Постоянное развитие и совершенствование самих численных методов, и расширение сферы их применения требует развития и разработки алгоритмов генерации сеток. Наработанный материал позволяет сделать выбор основной идеи алгоритма и характеристик, которыми он должен обладать. Хотя в конечном итоге конкретная сфера и цель применения определяют необходимые требования к алгоритму и генерируемой сетке.
В общем случае МКЭ позволяет решать задачи в двухмерной (2D) и трехмерной (3D) постановках. Использовать в нем можно прямолинейные и криволинейные конечные элементы. В двухмерных задачах применяются треугольники и четырехугольники, в трехмерных - тетраэдры, призмы и параллелепипеды. Кроме того, прямолинейные элементы всегда двухузловые, а криволинейные элементы могут быть трехузловыми и четырехузловыми (имеется в виду число узлов на каждом ребре). Несмотря на такое разнообразие элементов, чаще всего используются линейные треугольные элементы. Их легче генерировать и использовать, ими можно хорошо дискретизировать криволинейные объекты вместо использования криволинейных элементов. В МКЭ генерация сетки является задачей, не зависимой от остальных процессов, и требования к быстродействию не столь высоки. Более важными являются характеристики генерируемой сетки конечных элементов и требования к геометрической форме исследуемых объектов.
Требования, которым должен удовлетворять современный алгоритм генерации трехмерной конечно элементной сетки.
Прежде всего, генератор должен обслуживать исследуемые объекты, обладающие следующими характеристиками:
- - объектов может быть несколько; - они должны быть трехмерными и твердотельными, то есть физические характеристики объекта предполагаются неизменными в любой точке объекта; - объекты могут быть произвольной формы - выпуклые и невыпуклые, содержать криволинейные поверхности и линии, иметь различные сквозные отверстия; - должно учитываться взаимное расположение объектов и их расположение относительно центра координат.
Характеристики генерируемой сетки и элементов следующие: элементы должны быть тетраэдрами и обладать хорошим коэффициентом формы; сетка должна быть сбалансированной и единой для всей группы исследуемых объектов.
Сам алгоритм должен: использовать возможности САПР, в которой он будет работать, и обеспечивать хорошее быстродействие.
В основу алгоритма положена идея из [5], состоящая в том, чтобы разделить исследуемые объекты с помощью генерируемых кубов на множество компонентов, удовлетворяющих определенным требованиям, а затем эти компоненты разделить на тетраэдры (конечные элементы), которые и составят трехмерную треугольную сетку. Основной структурой данных алгоритма является восьмеричное дерево, состоящее из узлов.
С каждым узлом связывается выпуклый многоугольник, представляющий собой трехмерный куб, пересекающий один из исследуемых объектов. Все кубы строго ориентированы по осям общей системы координат. Каждый узел дерева может быть либо концевой вершиной, либо содержащим восемь узлов-потомков. Укладка из восьми потомков представляет собой восемь кубов, занимающих тот же объем. Логически эта укладка получается с помощью деления куба владельца пополам по каждому измерению. Любой из узлов-потомков также может быть либо концевой вершиной, либо укладкой из восьми своих потомков. Узел может содержать список узлов-дубликатов.
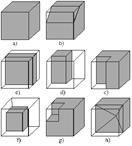
Рис.17. Простые компоненты.
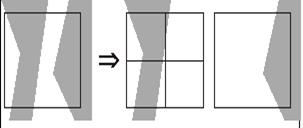
Рис.18. Создание дубликата.
Каждый из узлов может быть дублирован несколькими узлами-дубликатами. Дубликат - это точная копия узла, которая создается всякий раз, когда пересечение куба основного узла с исследуемыми объектами имеет несколько отдельных компонентов. Такое возможно при наличии нескольких объектов исследования и отверстий в них. Каждый дубликат связан только с одним компонентом пересечения (рис.18). При этом все дубликаты в алгоритме рассматриваются как самостоятельные узлы и также могут делиться.
Для функционирования алгоритма важны еще две категории узлов.
Соседними называются узлы, кубы которых имеют хотя бы одну общую точку. Примыкающими называются соседние узлы, компоненты, пересечения которых имеют хотя бы одну общую точку. Таким образом, первая фаза алгоритма генерации трехмерной сетки выглядит следующим образом.
Для начала необходимо указать объекты, которые будут исследоваться. Используя размеры и положение выбранных объектов, определяют размер и положение первого куба, который должен охватывать собой эти объекты. Первый куб является и первым узлом восьмеричного дерева. Начиная с этого узла, генерируется дерево.
На каждом шаге генерации дерева находится пересечение куба данного узла с исследуемыми объектами, при необходимости узел дублируется и делится. Процесс рекурсивно продолжается до тех пор, пока все концевые вершины не станут защищенными узлами. Защищенным называется узел, содержащий простой компонент, который не нужно делить. Узел, не пересекающий ни одного объекта, удаляется из дерева.
В процессе генерации дерева каждый узел делится, если:
- - размер куба больше заданного максимального размера; - компонент пересечения не является простым компонентом; - компонент простой, но его центр масс находится за пределами самого компонента; - компонент простой, но узкий - центр масс куба не находится в пределах компонента; - компонент простой, но его грани содержат внутренние контуры; - размер куба больше размера линеаризации, при условии, что компонент простой и содержит криволинейные поверхности.
Цель деления узлов и генерации дерева - разделить исследуемые объекты на малые и простые компоненты, которые затем было бы просто разделить на тетраэдры.
Простыми компонентами называются компоненты пересечения какого-либо куба с исследуемыми объектами, удовлетворяющие следующим требованиям:
- - компонент равен кубу (рис. 17a); - внутри куба находится одна грань компонента (рис. 17b); - внутри куба находится одно ребро компонента и две образующие ребро грани (рис. 17e, d); - внутри куба находится одна вершина компонента и несколько образующих вершину граней (рис. 17f, g, h).
Первая фаза алгоритма выглядит довольно простой, однако в ней есть несколько особенностей, порождающих большие последствия. Это связано с высокими требованиями, предъявляемыми к генерируемой сетке.
Первой проблемой (и на это указывают исследователи [3,4]) является наличие у объектов криволинейных поверхностей. У многих исследователей она вызывает большие трудности, но в основном из-за того, что они одновременно решают задачу ввода и обработки геометрической формы объектов. В нашем случае проблема решена довольно легко введением размера линеаризации, который по сути является шагом дискретизации кривых линий. Так как всю работу с геометрической формой объектов берет на себя САПР, и структура алгоритма генерации тетраэдров из простых компонентов такова, что новые узлы не создаются, а используются только существующие вершины компонентов, на фазе деления объектов происходит автоматическая линеаризация кривых и поверхностей.
Второй важной проблемой является коэффициент формы генерируемых тетраэдров. Тетраэдры не должны иметь очень острые углы и по форме должны быть как можно ближе к равносторонним тетраэдрам. Для МКЭ очень важно, чтобы сетка была сбалансированной. Качество конечных элементов и сбалансированность сетки очень сильно определяют качество дальнейших расчетов в МКЭ [1], особенно при необходимости добиться от метода высокой точности и сходимости. Сбалансированности генерируемой сетки можно достичь, если каждый узел в дереве будет удовлетворять условию баланса.
Условие баланса. Каждый соседний узел непременно делится, если он больше данного узла более чем в два раза. Это условие можно ввести еще на стадии деления узлов, а можно оформить отдельной операцией после фазы деления. В результате в сетке не образуются "дыры" - большой тетраэдр, окруженный маленькими тетраэдрами.
Коэффициент формы неявно учитывается во многих местах алгоритма. Это отказ от узких компонентов, выпуклость формы компонентов, близость формы компонентов к кубу. Учитывается он и на фазе генерации тетраэдров.
На практике в связи с коэффициентом формы выявилась такая проблема, которая не обсуждается в литературе. Дело в том, что в процессе деления узлов могут появиться компоненты с гранями, контур которых невыпуклый (рис. 2e, g). В этих случаях грани трудно триангулировать. Генерируемые тетраэдры получаются острыми и не образуют форму исходного компонента. Усиленное деление такого узла не только измельчает сетку и перегружает алгоритм, но и не имеет полного эффекта. Такой узел остается, и его приходится каким-то образом "линеаризовать". Для этого необходимо выявить подобные узлы и разделить компоненты на выпуклые элементы, например, их внутренними плоскостями.
Программная реализация первой фазы алгоритма не вызывает больших трудностей. Так, для генерации кубов, пересечения объектов, определения центров масс и выпуклости граней и других геометрических операций можно использовать библиотечные функции и объекты. Для определения простого компонента можно определять количество граней и вершин компонента, находящихся внутри куба, но не учитывать ребра. В этом случае компонент на рисунке 2c оказывается в группе с внутренним ребром, но это не оказывает никакого влияния на вторую фазу алгоритма.
Вторая фаза алгоритма генерирует тетраэдры из простых компонентов, полученных в первой фазе. Суть этой фазы состоит в том, чтобы разделить каждую грань компонентов на плоские треугольники, а затем добавить к ним центры масс компонентов в качестве четвертой вершины. В результате получаются тетраэдры.
Требований к треугольникам только два: они должны покрывать полностью всю грань и быть по форме близкими к равносторонним треугольникам. Если усиленно добиваться идеального коэффициента формы и для этого, проводя математические вычисления, добавлять новые вершины в компонент, то алгоритм станет сильно перегруженным. Быстродействие тоже является важной характеристикой алгоритма. Необходимо оптимальное решение. К тому же необходимо учесть, что в МКЭ не может быть независимой сетки для каждого исследуемого объекта, тем более если объекты соприкасаются и образуют границу раздела сред. Узлы, получаемые на такой границе, должны относиться к обоим объектам. При создании новых узлов их необходимо переносить и на компоненты соседних объектов.
В силу этого целесообразней использовать только существующие вершины. Более того, следует еще привести в соответствие все существующие вершины на всех компонентах, чтобы в сетке не появились пробелы - области объектов, не занятые тетраэдрами. Для этого необходимо провести предварительную процедуру по добавлению вершин. Для каждого узла необходимо отыскать примыкающие узлы и добавить компоненту данного узла вершины компонента примыкающего узла, отсутствующие у первого. В этом случае сетка гарантирована от пробелов.
Что касается триангуляции граней, то, как уже указывалось, наработаны алгоритмы двухмерной триангуляции плоских объектов, хотя и слишком общие для данной задачи. Для нашей задачи квалифицированный специалист может разработать свой алгоритм, более удовлетворяющий его.
Авторы использовали два алгоритма. В одном берется центр грани и от него проводятся лучи ко всем вершинам. А во втором вершины обходятся по спирали и соединяются в треугольники. Разные алгоритмы использовались для различных узлов, с целью лучшего баланса сетки.
На последнем этапе треугольники каждого компонента формируются в тетраэдры с помощью центра масс компонента. При этом следует учесть два момента. Во-первых, так как еще на этапе деления объектов проверяется условие нахождения центра масс, в пределах компонента, то никаких неожиданностей с формированием тетраэдров не возникнет. Во-вторых, при формировании сетки из тетраэдров необходимо учитывать, что МКЭ использует не сами тетраэдры, а узлы сетки и, соответственно, глобальную нумерацию узлов сетки для всей группы исследуемых объектов. Нумерация узлов сетки - важный момент в применении МКЭ, от нее зависит разреженность глобальной матрицы уравнений. Поэтому необходимо реализовать либо отдельную процедуру нумерации, либо при формировании сетки сразу нумеровать узлы сетки.
Таким образом, разработан практичный и простой в реализации алгоритм генерации трехмерной сетки. Основными достоинствами алгоритма являются:
- - отсутствие ограничений на геометрическую форму исследуемых объектов; - высокое качество генерируемой сетки элементов; - простота реализации.
Алгоритм не отличается высоким быстродействием. Однако следует учитывать, что быстродействие программы зависит от производительности компьютера. Поэтому авторы не посчитали этот критерий столь существенным. Алгоритм опробован на практике и удовлетворяет сформулированным требованиям.
Разработка технического задания на программу
Назначение и область применения.
Программа предназначена для разбиения конструкций сеткой на плоские конечные элементы.
Описание объектов проектирования.
Конструкция представлена в виде плоской фигуры, которую в дальнейшем разбивают на плоские конечные элементы. Разбиение производится с определенной погрешностью, которую задает пользователь.
Похожие статьи
-
Описание основных возможностей МКЭ МКЭ представляет собой эффективный метод решения инженерных задач. Область применения метода от анализа напряжений в...
-
Введение - Программное обеспечение расчета конструкций
Метод конечных элементов является одним из наиболее распространенных методов решения задач математической физики. Это связано с большой универсальностью...
-
Типы конечных элементов - Программное обеспечение расчета конструкций
Простейшим среди элементов является одномерный элемент. Схематически он обычно изображается в виде отрезка, хотя и имеет поперечное сечение. Площадь...
-
Для реализации поставленной задачи методом конечных элементов будут использованы следующие программные обеспечения (ПО): - MATLAB - ПО и одноименный язык...
-
Рис. 9 Пример B+ дерева, связывающего ключи 1-7 с данными d1-d7. Связи (выделены красным) позволяют быстро обходить дерево в порядке возрастания ключей....
-
Общее описание программного обеспечения, реализующего разработанный алгоритм Основной идеей дипломного проекта, является реализация алгоритма...
-
Теоретические аспекты поставленной задачи В этой части проекта будут объяснены этапы применения МКЭ для плоской фермы. В первой главе было рассмотрено...
-
ЛИРА - Программное обеспечение расчета конструкций
Программный комплекс ЛИРА-САПР является современным инструментом для численного исследования прочности и устойчивости конструкций и их...
-
Существует множество систем конечно-элементных расчетов, таких как ANSYS, NASTRAN, ЛИРА. ANSYS Технологии компьютерного моделирования ANSYS позволяют...
-
Цель Работы - научиться использовать операции динамического выделения и освобождения памяти на примере работы с одномерными и двумерными массивами, а...
-
Каждая диаграмма состояний в UML описывает все возможные состояния одного экземпляра определенного класса и возможные последовательности его переходов из...
-
Кластеризация (или кластерный анализ) -- это задача разбиения множества объектов на группы, называемые кластерами. Внутри каждой группы должны оказаться...
-
Понятие Data Mining Средства Data Mining включают в себя очень широкий класс различных технологий и инструментов. Средства Data Mining на рынке...
-
Рис. 7 Пример двоичного дерева поиска Двоичное дерево поиска (binary search tree, BST) -- это двоичное дерево, для которого выполняются следующие...
-
NASTRAN - Программное обеспечение расчета конструкций
NASTRAN - это одна из лучших на рынке конечно-элементная система. MSC Nastran вот уже более 40 лет доказывает свою точность и эффективность. Постоянно...
-
Коллекция транзакций хранится в файле на диске. Алгоритм читает каждую транзакцию t последовательно и присоединяет t к существующему кластеру, или...
-
Цель Работы - изучить основные способы работы с пользовательским типом данных "класс", его объектами, методами и способы доступа к ним. - Теоретические...
-
В работе использовались следующее программное обеспечение для решения поставленных задач: AutoCAD, ANSYS Workbench, ANSYS Icepak. Система AutoCAD...
-
Метод конечных элементов является численным методом для нахождения приближенных решений физических задач. В основе этого метода лежит разделение...
-
Метод конечных элементов (МКЭ) жесткости возник в аэрокосмической отрасли. Исследователи рассматривали различные подходы к анализу сложных частей...
-
Допустим, что MinSupi = и * |Ci|. Поддержка данного предмета в Ci характеризует число транзакций в этом кластере, которые содержат этот предмет. Поэтому...
-
В данной части работы будут рассмотрены основные бизнес-процессы этапа разработки программного обеспечения в рамках учебных проектов в университете. В...
-
Подход, основанный на "больших" предметах и функциональный критерий кластеризации Поддержка предмета в кластере Ci есть относительное число транзакций в...
-
Термин "транзакция" относится к подмножеству предметов из общей совокупности с переменным числом предметов (мощностью подмножества). Транзакциями...
-
Вычислительная сложность алгоритмов Алгоритм кластеризации Вычислительная сложность Иерархический O(n2) K-средних O(nkl), где k - число кластеров, l -...
-
Данная глава посвящена описанию автоматизированного тестирования, его типам, выявлению достоинств и недостатков в автоматизации тестирования. Более того...
-
Для того, чтобы использовать симметричные алгоритмы шифрования, необходимо безопасно обменяться ключами. Протокол Диффи - Хеллмана позволяет двум и более...
-
В наше время все большее количество компаний, стремясь к повышению эффективности и прибыльности бизнеса пользуются цифровыми (автоматизированными)...
-
Базовый интерфейс двоичного дерева поиска состоит из трех операций: - FIND(K) -- поиск узла, в котором хранится пара (key, value) с key = K. - INSERT(K,...
-
IDEF0 - графическая нотация, предназначенная для формализации и описания бизнес-процессов. Отличительной особенностью IDEF0 является ее акцент на...
-
Работа с программой будет начинаться с отображения главного меню программы и дисков компьютера в дереве папок. Далее мы сможем выбрать на какой диск...
-
Модернизация обобщенного алгоритма кластеризации состоит в использовании вместо обычных бинарных деревьев сбалансированных бинарных деревьев(B+ tree)....
-
1.1 Характеристика предметной области Программный обеспечение база данные Представим предметную область "Программное обеспечение ЦЗН" как взаимодействие...
-
Алгоритм для обновления дан на рис.6. Для каждого предмета е в t отыскивается Hashi. Если е найдено хэше кластера, то увеличиваем на 1 его sup в Btreei....
-
Программы-оболочки - Программное обеспечение компьютера
Операционная система МS-DOS позволила успешно работать с персональными компьютерами на протяжении почти 15 лет. Тем не менее, эту работу нельзя назвать...
-
Модификации алгоритма Лемпеля-Зива, предложенная Терри Уэлчем - Анализ алгоритма Лемпеля-Зива
В 1984 году Терри Уэлч (Terry Welch) предложил адаптивный сброс словаря для алгоритма LZ78 [3]. В этом случае при заполнении словаря сброс словаря не...
-
Наиболее распространенной реализацией МКЭ является метод прямой жесткости, применяемый для компьютерного моделирования сложных структур. Это матричный...
-
Для оценки возможности выполнения проекта имеющимся в распоряжении разработчика штатным составом исполнителей, нужно рассчитать их среднее количество,...
-
Рассмотрим особенности программирования под Android. Класс Activity - самый важный класс, из которого строится приложение Android. Этот класс...
-
Цель Работы - изучить приемы создания и использования шаблонов классов. - Теоретические сведения Достаточно часто встречаются классы, объекты которых...
Анализ алгоритмов построения сеток - Программное обеспечение расчета конструкций