Типовые дискретные звенья - Теория дискретных систем

Сложную передаточную функцию дискретной системы удобно представлять в виде произведения передаточных функций типовых звеньев не выше второго порядка, как это делалось для непрерывных систем. Так как передаточная функция К*(z), записанная формулой (1.23), по своей структуре аналогична передаточной функции непрерывной системы

Kyx(p) = y(p)

X(p) = b0 + b1 p + ... + bm pm

C0 + c1 p + ... + cn pn = P(p)

D(p)

Где роль р играет разностный оператор (1-z-1), то выражения типовых дискретных звеньев остаются похожими на соответствующие выражения непрерывных. Классификация типовых дискретных звеньев и некоторые их характеристики даются в табл. П. 4. Аналогия между дискретными и непрерывными звеньями имеет не только внешний, но и существенный характер. Особенно наглядно это видно на примере частотных характеристик, которые для дискретных звеньев получаются заменой z = e jщTn в передаточной функции К*(z). Особенность этих выражений состоит в том, что параметр ф в них является безразмерной величиной, поскольку оператор (1 - z-1) также не имеет размерности. Называть поэтому параметр ф постоянной времени можно лишь условно. Несмотря на указанное отличие, между типовыми дискретными и непрерывными звеньями существует глубокая аналогия, которая наглядно видна при сравнении частотных характеристик. Напомним, что для получения частотной характеристики дискретной системы надо в передаточной функции К*(z) заменить

Z = e jщTn

Или вместо разностного оператора (1 - z-1) взять

(1 - e - jщTn).

Если щTn << 1, что соответствует низким частотам щ << Щ, то оператор

1 - e - jщTn > jщTn,

А это приводит к практически полному совпадению с частотными характеристиками типовых непрерывных звеньев с постоянной времени

T = ф Tn,

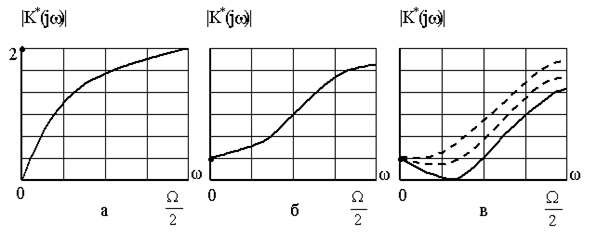
Таким образом, в области щ, близких к нулю, частотные характеристики дискретных совпадают с характеристиками соответствующих непрерывных звеньев. Так, например, при щ = 0 частотная характеристика суммирующего (дискретного интегрирующего) звена равна K*(jщ) = ?, а апериодического и колебательного звеньев - единице. С ростом частоты щ от 0 до амплитудно-частотные характеристики этих звеньев уменьшаются. В дальнейшем они меняются периодически вдоль оси щ с периодом. На рисунке 1.14 показаны АЧХ: а-суммирующего, б-апериодического, в-колебательного звена при различных значениях параметра о. Идеальное разностное (дискретное дифференцирующее) звено при щ = 0 имеет K*(jщ) = 0, а разностные первого и второго порядка -1. То же самое имеет место и у соответствующих непрерывных звеньев. С ростом частоты щ от 0 до АЧХ разностных звеньев возрастает, что и показано на рис. 1.15 для идеального разностного звена (а), разностного звена первого порядка (б) и разностного звена второго порядка (в). Зная характер поведения частотных характеристик типовых дискретных звеньев, можно судить о желаемой структуре дискретной следящей системы и, следовательно, о ее желаемой передаточной функции.

Рис. 1.15 Амплитудно-частотные характеристики разностных дискретных звеньев

Частотные характеристики и структурная схема дискретной следящей системы

Дискретная следящая система (рис. 1.16) предназначена для воспроизведения задающего воздействия х(iТn), и в идеальном случае выходной процесс в ней должен равняться входному, то есть

Y(iTn) = x(iTn)

Выполнению этого равенства препятствуют два фактора: наличие возмущающих воздействий и инерционность системы. Оба эти фактора существенно влияют на выбор формы частотной характеристики замкнутой системы.

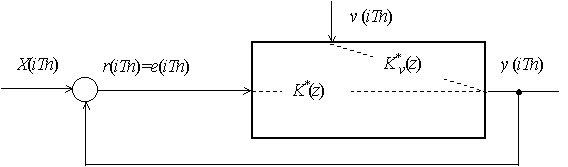
Рис. 1.16 Линейная дискретная следящая система

Частотный спектр задающего воздействия х*(jщ) расположен в области низких частот и имеет граничную частоту щгр ( рис. 1.17). В соответствии с теоремой Котельникова, частота квантования сигнала должна удовлетворять условию Щ > щгр.

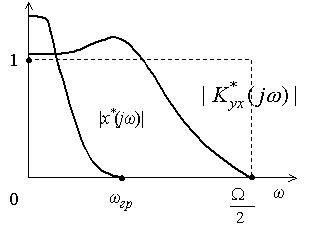
Рис. 1.17 Амплитудно-частотная характеристика дискретной следящей системы

Для достаточно полного воспроизведения спектра задающего воздействия на фоне широкополосных помех частотная характеристика замкнутой следящей системы K*yx(jщ) должна быть близка к 1 в диапазоне 0 ? щ ? щгр и к нулю - в диапазоне щгр < щ ? . Этому условию, в частности, удовлетворяет кривая амплитудно-частотной характеристики |K*yx(jщ)| на рис. 1.17. Стремлению K*yx(jщ) > 0 при щ > соответствуют и условия естественной инерционности элементов САУ. В итоге, если рассматривать всю область частот, АЧХ замкнутой дискретной следящей системы должна иметь вид, показанный на рис. 1.18, то есть соответствовать характеристике гребенчатого фильтра.

Дискретный система функция

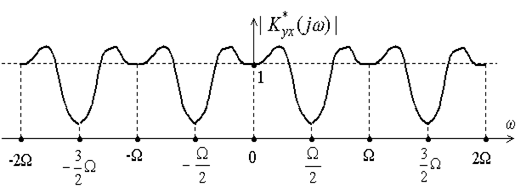
Рис. 1.18Амплитудно-частотная характеристика гребенчатого фильтра

Чтобы получить заданную K*yx(jщ), надо сформировать вполне определенную частотную характеристику разомкнутой системы (рис. 1.16) K*(jщ). Очевидно, что требования к последней аналогичны тем требованиям, которые предъявляются к частотным характеристикам разомкнутых непрерывных следящих систем.

Так, чтобы обеспечить равенствоK*yx(jщ) ? 1 на частотах щ = 0 и щ, кратных Щ (см. рис. 1.18), необходимо иметь K*(jщ) > 0, что достигается включением в состав системы суммирующих (дискретных интегрирующих) звеньев или усилительных звеньев с очень большим коэффициентом усиления. Чтобы обеспечить условие K*yx(jщ) > 0 при щ > в состав разомкнутой системы надо включать инерционные (апериодические или колебательные) звенья. Согласование хода частотных характеристик в указанных областях может быть обеспечено разностными (дискретными дифференцирующими) звеньями.

Анализ частотных характеристик показывает, что структура дискретной следящей системы, определяемая звеньями, входящими в состав разомкнутой системы, аналогична структуре непрерывных следящих систем и соответственно аналогичны и передаточные функции сравниваемых систем. Передаточная функция дискретной разомкнутой следящей системы (рис. 1.16), например, может быть получена из разностного уравнения, записанного в конечно-разностной форме

^a0 y(iTn) +^a1

Д1 y(iTn) + ... +^

An Дn y(iTn) =^

B0 r(iTn) +^

B1 Д1 r(iTn) + ... +^

Bm Дm r(iTn) (1.28)

В виде

K*(z) = ^

B0 + ^

B1 (1 - z-1) + ... + ^

Bm (1 - z-1)m = P*(z) (1.29)

^a0 + ^

A1 (1 - z-1) + ... ^

An (1 - z-1) Q*(z)

В выражениях (1.28) и (1.29) коэффициенты и определяются параметрами дискретной системы. Порядок астатизма н определяется количеством коэффициентов 0 = 1 = ... = н - 1= 0 или, что одно и то же, количеством суммирующих звеньев.

Уравнение замкнутой следящей системы получается из выражения (1.28) путем замены r(iTn) = x(iTn) - y(iTn) и после группировки слагаемых принимает вид

^c0 y(iTn) + ^

C1 Д1 y(iTn) + ... + ^

Cn Дn y(iTn) = ^ b0y(iTn) +^

B1 Д1 y(iTn) + ... +^

Bm Дm y(iTn) (1.30)

Где коэффициенты

= + .

Передаточная функция замкнутой системы, получаемая из формулы (1.30) или по рис. 1.16, оказывается равной

K*yx(z) = K*(z) = ^

B0 + ^b1 (1 - z-1) + ... + ^ bm(1 - z-1)m = P*(z.) (1.31)

1 + K*(z) ^ c0 + ^

C1 (1 - z-1) + ... + ^ cn (1 - z-1)n D*(z)

Где полином знаменателя

D*(z) = P*(z) + Q*(z).

В следящих системах ошибка e(iTn) совпадает с рассогласованием r(iTn) и, следовательно, передаточная функция ошибки по задающему воздействию согласно рис. 1.16 равна

K*ex(z) = 1 - K*yx(z) = 1 = ^

A0 + ^ a1(1 - z-1) + ... + ^ an(1 - z-1)n = Q*(z) (1.32)

1 + K*(z) ^ c0 + ^

C1 (1 - z-1) + ... + ^

Cn (1 - z-1)n D*(z)

Передаточная функция ошибки по возмущающему воздействию, как и в непрерывных системах, равна

K*ev(z) = - K*yv(z),

То есть с точностью до знака совпадает с передаточной функцией системы по этому воздействию и согласно рис. 1.16 равна

K*ev(z) = - K*yv(z) = K*v(z)

1 + K*(z) (1.33)

Где K*v(z) - передаточная функция по возмущающему воздействию разомкнутой системы.

Таким образом, соотношения (1.28) - (1.33) для дискретных следящих систем имеют ту же структуру, что и соответствующие им соотношения для непрерывных следящих систем.

Отметим, что если исходное уравнение разомкнутой следящей системы (1.28) записывается в рекуррентной форме (см. п. 1.3)

A0 y(iTn) + a1 y[(i-1)Tn] + ... + an y[(i-n)Tn] =

= b0 r(iTn) + b1 r[(i-1)Tn] + ... + bm r[(i-m)Tn],

То уравнение замкнутой примет вид

C0 y(iTn) + c1 y[(i-1)Tn] + ... + cn y[(i-n)Tn] =

= b0 x(iTn) + b1 x[(i-1)Tn] + ... + bm x[(i-m)Tn] (1.34)

При этом полиномы P*(z), Q*(z) и D*(z) меняют свою структуру и передаточные функции дискретной следящей системы записываются в следующем виде

K(z) = b0 + b1 z-1 + ... + bm z-m

A0 + a1 z-1 + ... + an z-n =P*(z)

Q*(z) (1.35)

K^yx(z) = b0 + b1 z-1 + ... + bm z-m

C0 + c1 z-1 + ... + cn z-n = P*(z)

D*(z) (1.36)

K^ex(z) = a0 + a1 z-1 + ... + an z-n

C0 + c1 z-1 + ... + cn z-n = Q*(z)

D*(z) (1.37)

Использование передаточных функций следящих систем в виде соотношений (1.29), (1.31) и (1.32) или соотношений (1.35) - (1.37) определяется характером решаемой задачи.

Тестовые сигналы (test signal). В качестве тестовых сигналов, которые применяются при моделировании и исследовании систем обработки данных, обычно используются сигналы простейшего типа: гармонические синус-косинусные функции, дельта-функция и функция единичного скачка.

Дельта-функция или функция Дирака. По определению, дельта-функция описывается следующими математическими выражениями (в совокупности):

?(t-?) = 0 при t ? ?, ?(t-?) dt = 1.

Функция ?(t-?) не является дифференцируемой, и имеет размерность, обратную размерности ее аргумента, что следует из безразмерности результата интегрирования. Значение дельта-функции равно нулю везде за исключением точки ?, где она представляет собой бесконечно узкий импульс с бесконечно большой амплитудой, при этом площадь импульса равна 1.

Дельта-функция является полезной математической абстракцией. На практике такие функции не могут быть реализованы с абсолютной точностью, так как невозможно реализовать значение, равное бесконечности, в точке t = ? на аналоговой временной шкале. Но во всех случаях, когда площадь импульса равна 1, длительность импульса достаточно мала, а за время его действия на входе системы сигнал на ее выходе практически не изменяется (реакция системы на импульс во много раз больше длительности самого импульса), входной сигнал можно считать единичной импульсной функцией со свойствами дельта - функции.

При своей абстрактности дельта - функция имеет вполне определенный физический смысл. Представим себе импульсный сигнал прямоугольной формы П(t-) длительностью, амплитуда которого равна 1/, а площадь соответственно равна 1. При уменьшении значения длительности импульс, сокращаясь по длительности, сохраняет свою площадь, равную 1, и возрастает по амплитуде. Предел такой операции при 0 и носит название дельта - импульса. Этот сигнал ?(t-?) сосредоточен в одной координатной точке t = ?, конкретное амплитудное значение сигнала не определено, но площадь (интеграл) остается равной 1. Это не мгновенное значение функции в точке t = ?, а именно импульс (импульс силы в механике, импульс тока в электротехнике и т. п.) - математическая модель короткого действия, значение которого равно 1.

Дельта-функция обладает фильтрующим свойством. Суть его заключается в том, что если дельта-функция ?(t-?) входит под интеграл какой-либо функции в качестве множителя, то результат интегрирования равен значению подынтегральной функции в точке ? расположения дельта-импульса, т. е.:

S(t) ?(t-?) dt = s(?).

Интегрирование в выражении может ограничиваться ближними окрестностями точки ?.

Функция единичного скачка или функция Хевисайда иногда называется также функцией включения. Полное математическое выражение функции:

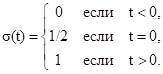
При моделировании сигналов и систем значение функции скачка в точке t=0 очень часто принимают равным 1, если это не имеет принципиального значения.

Функция единичного скачка используется при создании математических моделей сигналов конечной длительности. При умножении любой произвольной функции, в том числе периодической, на прямоугольный импульс, сформированный из двух последовательных функций единичного скачка

S(t) = (t) - (t-T)

Из нее вырезается участок на интервале 0-Т, и обнуляются значения функции за пределами этого интервала.

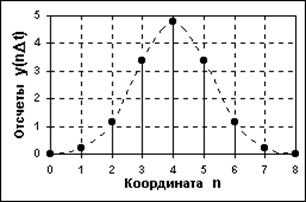
Рис. 1.2.2 Дискретный сигнал

Дискретный сигнал (discrete signal) по своим значениям также является непрерывной функцией, но определенной только по дискретным значениям аргумента. По множеству своих значений он является конечным (счетным) и описывается дискретной последовательностью отсчетов (samples) y(n?t), где y1 ?y y2, ?t - интервал между отсчетами (интервал или шаг дискретизации, sample time), n = 0, 1, 2,...,N. Величина, обратная шагу дискретизации: f = 1/?t, называется частотой дискретизации (sampling frequency). Если дискретный сигнал получен дискретизацией (sampling) аналогового сигнала, то он представляет собой последовательность отсчетов, значения которых в точности равны значениям исходного сигнала по координатам n?t.

Пример дискретизации аналогового сигнала (рис. 1.2.1) представлен на рис. 1.2.2. При ?t = const (равномерная дискретизация данных) дискретный сигнал можно описывать сокращенным обозначением y(n). В технической литературе в обозначениях дискретизированных функций иногда оставляют прежние индексы аргументов аналоговых функций, заключая их в квадратные скобки - y[t]. При неравномерной дискретизации сигнала обозначения дискретных последовательностей обычно заключаются в фигурные скобки - {s(ti)}, а значения отсчетов приводятся в виде таблиц с указанием значений координат ti. Для числовых последовательностей (равномерных и неравномерных) применяется и следующее числовое описание: s(ti) = {a1, a2, ..., aN}, t = t1, t2, ...,tN. Примеры дискретных геофизических сигналов - результаты вертикального электрического зондирования (дискретная величина разноса токовых электродов), профили геохимического опробования, и т. п.

Операция дискретизации (discretization) осуществляет преобразование аналоговых сигналов (функций), непрерывных по аргументу, в функции мгновенных значений сигналов по дискретному аргументу. Дискретизация обычно производится с постоянным шагом по аргументу (равномерная дискретизация), при этом s(t) ??s(n?t), где значения s(n?t) представляют собой отсчеты функции s(t) в моменты времени t = n?t, n = 0, 1, 2,..., N. Частота, с которой выполняются замеры аналогового сигнала, называется частотой дискретизации. В общем случае, сетка отсчетов по аргументу может быть произвольной, как, например, s(t)???s(tk), k=1, 2, ..., K, или задаваться по определенному закону.

В результате дискретизации непрерывный (аналоговый) сигнал переводится в последовательность чисел.

Типовые дискретные звенья - Теория дискретных систем

Похожие статьи