Критерии согласия - Измерения параметров сигнала
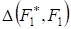
В предыдущих случаях при синтезе алгоритмов оценок параметров, алгоритмов обнаружения или различения сигналов предполагалось наличие априорной информации относительно распределения сигналов или помех. Однако в большинстве практических ситуаций при выполнении перечисленных операций плотность вероятности неизвестна. Можно лишь делать разного рода предположения. В такой ситуации необходимо, располагая выборочными значениями, сделать статистический вывод относительно вида функции распределения, из которого извлечена выборка. Представляет интерес ввести количественную меру соответствия гипотетического и эмпирического распределений, или, как говорят, критерий согласия. Этот критерий представляет число, которое является функционалом от эмпирического и гипотетического F1 распределений.
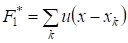
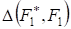
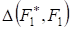
Сформулированная задача решается в следующей последовательности. По выборочным значениям X строится эмпирическая функция распределения по формуле, где - единичный скачок. На основании этого эмпирического распределения, но, может быть, и из других соображений, выдвигается гипотеза о том, что выборка извлечена их совокупности с распределением F1(X). По принятому заранее критерию согласия необходимо вычислить и вероятность того, что указанная величина превосходит некоторое пороговое значение. Для этого необходимо знать распределение величины. Определить такое распределение в простой форме удается, как правило, лишь при больших размерах выборки (точнее, определить лишь асимптотическое распределение при ). Если распределение величины известно, то, задаваясь вероятностью (уровнем значимости критерия) того, что, находим пороговое значение. При достаточно малом получаем приемлемое для практики правило проверки гипотезы об истинности гипотетического распределения F1(X): если для данной выборки, то гипотеза отвергается, в противоположном случае - принимается. При этом вероятность отвергнуть правильную гипотезу будет равна уровню значимости.
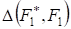
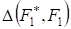
Отметим, что распределение величины, определяемое при условии, что выборочные значения X, по которым построена, извлечены из совокупности с распределением F1, зависит от F1. Было бы желательно иметь такие критерии согласия, распределения которых не зависели бы от вида F1. Такие критерии называются непараметрическими. Ниже рассмотрим критерии, которые при являются непараметрическими (асимптотически).
Следует также иметь в виду, что такие критерии согласия дают при достаточно малом достаточно эффективное решающее правило, позволяющее отвергнуть неверную гипотезу. При этом, однако, остается неизвестной вероятность ошибок второго рода - принятие неверной гипотезы. Если для данной выборки, то, хотя принятое правило предписывает утверждать истинность выдвинутой гипотезы, следует к такому утверждению отнестись более осторожно, так как с учетом заданного критерия согласия нет оснований считать, что выборка X не согласуется с гипотетическим распределением.
Недостатком критериев согласия является произвольность выбора самого критерия и уровня значимости, а также трудности, связанные с определением их распределений для малых N. Другой путь состоит в непосредственном построении неизвестной функции F1 по выборочным значениям без выдвижения гипотезы о виде этой функции.
5.1. Критерий - Пирсона. Этот критерий является одним из самых распространенных в приложениях к теории статистических оценок.
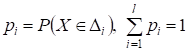
Разобьем область, где определена гипотетическая функция распределения F1(X) случайной величины X, на конечное число неперекрывающихся интервалов. Обозначим вероятность попадания единичного измерения в I-й интервал. Пусть в выборке X число выборочных значений, попадающих в интервал, равно. Ясно, что
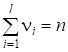
.
Используем в качестве критерия согласия величину
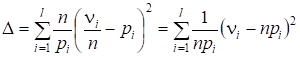
.
Как доказал Пирсон, если проверяемая гипотеза об истинности распределения F1(X) верна, то при распределение асимптотически приближается к - распределению с степенями свободы, Не зависящему от вида гипотетического распределения F1(X).
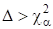
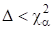
Итак, пусть - процентное отклонение случайной величины, имеющей - распределение с степенями свободы, т. е. . При достаточно малом и большом N величина, вычисленная согласно критерию - Пирсона, практически никогда не будет превосходить порогового значения, если только гипотеза о виде распределения верна. Таким образом, выбирается следующее правило проверки гипотезы: гипотеза отклоняется, если, и принимается, если. Вероятность отклонить верную гипотезу равна.
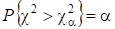
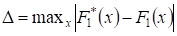
5.2. Критерий Колмогорова. Согласно этому критерию количественной мерой соответствия служит для заданного размера n выборки максимум по всем значениям x модуля отклонения эмпирического распределения от гипотетического, т. е. . Как доказал А. Н. Кол-могоров, если проверяемая гипотеза истинности F1(x) верна, то при и дополнительном предположении непрерывности F1(x) функция распределения величины асимптотически приближается к
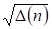
.
Если - заданный уровень значимости, то можно записать после некоторых преобразований:
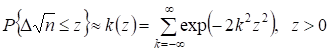
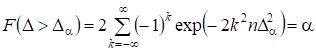
.
Этот ряд быстро сходится и в качестве первого приближения можно ограничиться только первым его членом, т. е.
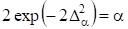
или
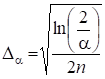
Следовательно, правило проверки гипотезы таково: если для наблюдаемой выборки, то гипотеза о том, что выборка извлечена из совокупности, имеющей гипотетическое распределение, отвергается; если имеет место противоположное неравенство, то гипотеза принимается. Таблицы значений функции приведены в [1]. Как и критерий - Пирсона, критерий Колмогорова используется при очень больших размерах N выборки. Однако при использовании этого критерия нет необходимости в предварительном распределении выборочных значений на интервалы и группировании, как это делается при использовании критерия - Пирсона.
5.3. Критерий Мизеса. Согласно этому критерию количественной мерой соответствия гипотетического и эмпирического распределений для заданного размера n выборки служит среднее значение квадрата отклонения указанных распределений
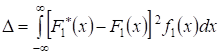
,
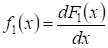
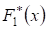
Где - гипотетическая плотность вероятности случайной величины X. Представив выражение для через сумму ступенчатых функций с весом, зависящим от N, и интегрируя полученное выражение, придем к следующей формуле:
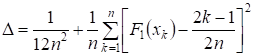
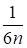
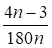
Математическое ожидание такой случайной величины есть, второй центральный момент имеет вид. Выражение для точного распределения величины очень сложное, но при оно близко к предыдущему. Как и критерий Колмогорова, критерий Мизеса в отличие от - Пирсона не связан с группированием выборочных данных, и его распределение достаточно быстро при увеличении N стремится к предельному распределению. Процентные точки предельного распределения имеют значения, представленные в табл. 2.
Таблица 2
|
0,5 |
0,4 |
0,3 |
0,2 |
0,1 |
0,05 |
0,03 |
0,02 |
0,01 |
0,001 |
|
0,12 |
0,15 |
0,18 |
0,24 |
0,35 |
0,46 |
0,55 |
0,62 |
0,744 |
1,17 |
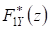
5.4. Оценка принадлежности двух выборок одному и тому же распределению. Пусть имеются выборки X и Y, полученные в результате независимых единичных измерений, каждая из которых принадлежит некоторому распределению. Необходимо проверить гипотезу о том, что обе эти выборки принадлежат одному и тому же распределению. Пусть и - эмпирические функции распределения, построенные по двум выборкам X и Y (размер выборки X есть n, а выборки Y - m). В качестве критерия согласия примем величину
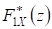
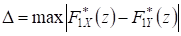
Как доказал Н. В. Смирнов, при вероятность
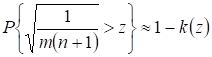
,
Где - функция, аналогичная функции, используемой в критерии Колмогорова. Если задан уровень значимости, то можно, как и в критерии Колмогорова, определить пороговое значение, с которым необходимо сравнивать рассчитанное :
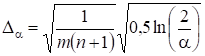
.
Таким образом, если, то выборки X и Y принадлежат одному и тому же распределению.
Другой критерий, предложенный Вилкоксоном, основан на подсчете числа инверсий. Для этого обе выборки располагают в виде порядковой статистики по возрастанию значений, например, Если в этой последовательности заданному X предшествуют S элементов выборки Y, то имеет место S инверсий. Общее число инверсий U равно сумме инверсий, образуемых всеми первыми элементами с элементами второй. Правило проверки гипотезы по критерию Вилкоксоном состоит в сравнении общего числа инверсий с пороговым числом, определяемым уровнем значимости.
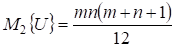
Доказано, что при и с хорошим приближением можно считать распределение общего числа инверсий нормальным с параметрами ; . Тогда пороговое значение U числа инверсий для заданного уровня значимости может быть определено по формуле
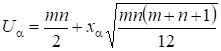
,
Где - процентное отклонение нормальной случайной величины. Если вычисленное по заданным двум выборкам значение U превосходит U, то гипотеза о том, что эти выборки принадлежат одному и тому же распределению, отклоняются.
Похожие статьи
-
Оценка параметров многомерной функции распределения - Измерения параметров сигнала
Параметр амплитуда сигнал 6.1. Обобщение основных определений на многомерные распределения. До сих пор мы изучали теорию оценок параметров или самих...
-
Методы получения оценок параметров - Измерения параметров сигнала
Многие важные задачи обработки сигналов сводятся к получению статистических выводов относительно всех или некоторых неизвестных параметров сигналов. При...
-
Интервальные оценки параметров сигналов - Измерения параметров сигнала
Как известно, точечные оценки параметров сигналов не позволяют оценить степень близости полученной оценки к истинному значению оцениваемого параметра....
-
Оценка неэнергетических параметров - Измерения параметров сигнала
Сигнал зависит от какого-либо неэнергетического параметра А , которым может быть задержка сигнала или смещение частоты (эффект Доплера в радиолокации)....
-
Оптимальная оценка амплитуды сигнала - Измерения параметров сигнала
Представим сигнал в таком виде: , Где А - оцениваемая амплитуда; C ( T ) - сигнал с единичной амплитудой. Тогда выборка содержит два слагаемых: , Где, в...
-
Данные передача сигнал сообщение Для обеспечения заданной достоверности при передаче данных применяют обратные связи и помехоустойчивое кодирование,...
-
1) Зафиксируем переход с черного поля на белое поле (или наоборот), см. рис.15 Рис. 15 2) Измерим амплитуду шума на черном поле, см. рис.16 (в данном...
-
Определение чувствительности производится с помощью измерительного генератора, уровень входного сигнала которого или нормирован с допускаемой для поверки...
-
Оптимизация по критерию максимума отношения сигнал/шум - Оптимальные линейные системы
Рассмотрим, аналогично 4.1.1, обработку сигнала на фоне "белого шума" , по-прежнему используя в качестве критерия оптимальности критерий максимума...
-
При последовательном возрастании значений входного цифрового сигнала D(t) от 0 до 2N-1 через единицу младшего разряда (ЕМР) выходной сигнал UВых(t)...
-
Рассмотрим задачу воспроизведения полезного сигнала, представленного реализацией случайного процесса, на фоне шума. По-прежнему энергетические спектры...
-
На втором этапе измерений речи артикуляционным методом проводится цикл измерений. Цикл измерений включает в себя результат приема всех аудиторов от всех...
-
Величина Кв при рівномірному квантуванні визначається Кв= 3L2/.(2.6) З цієї формули ми зможемо знайти число рівнів квантування L Кв. ? Кв. доп. Кв....
-
Использование тестовых сигналов - Структурные методы повышения точности средств измерения
Тестовые методы повышения точности измерений применяются в различных измерительных системах для измерений как электрических, так и неэлектрических...
-
Рассмотрим несколько конкретных примеров измерения параметров фильтра в полосных и гомоморфных вокодерах, а также в вокодерах с линейным предсказанием...
-
Рассмотрим обработку сигнала вида На фоне "белого шума" , имеющего энергетический спектр вида . В качестве критерия оптимальности выберем критерий...
-
Динамические параметры ЦАП определяются по изменению выходного сигнала при скачкообразном изменении входного кода, обычно от величины "все нули" до "все...
-
Экспериментальные исследования искажений сигнала производились двухмодовым и одномодовым методами. В качестве регистрирующей аппаратуры использовался...
-
Рисунок 3.2 - Детерминированные сигналы Сигналы подразделяются на непрерывные (аналоговые) и прерывистые (дискретные). Сигналы - аналоговые, они...
-
Скорость света: . Фазовая скорость распространения электромагнитных волн (ЭМВ) в произвольной среде: , Где --=-- _ - ,-- --=-- _ - ,...
-
1. На втором этапе измерений узнаваемости голоса диктора методом парных сравнений, определяется величина предпочтения одного из сравниваемых речевых...
-
Подготовка прибора к работе После включения, пятиминутного прогрева и проверки работоспособности прибора поставьте переключатель ДИОД-ТРАНЗИСТОР в...
-
Использование информационной избыточности - Структурные методы повышения точности средств измерения
Под информационной избыточностью понимается такое состояние измерительной информации, при котором она больше необходимой для реализации функций...
-
Измерение параметров элементов радиотехнических цепей (R, L, С, tgд=1/Q) - Оcновы радиоэлектроники
Метод вольтметра-амперметра Не требует специальных приборов (рис. 24). Рис. 24. Схема измерения комплексного сопротивления методом вольтметра-амперметра...
-
Обработка результатов прямого измерения - Измерение объективных характеристик видеооборудования
При проведении измерений хорошим тоном считается указание погрешности измерений (поскольку мы не можем измерять с абсолютной точностью величины) и...
-
Определение полос пропускания проводится с помощью измерительного генератора, электронно-счетного частотомера и измерителя уровня, которые подключаются к...
-
Ансамбли сигналов в СПДС - Сигналы в системе преобразования дискретной связи
Сигнал в СПДС представляет собой изменяющуюся физическую величину, отображающую сообщение или его элементы. В общем виде сигнал на выходе УПС (устройства...
-
Расчет числа разрядов АЦП. В результате равномерного квантования мгновенное значение непрерывной величины х представляют в виде конечного числа m...
-
ЛИТЕРАТУРА - Системы прямого цифрового синтеза сигналов. Параметры цифро-аналоговых преобразователей
Лидовский В. И. Теория информации. - М., "Высшая школа", 2002г. - 120с. Метрология и радиоизмерения в телекоммуникационных системах. Учебник для ВУЗов. /...
-
Методы измерения передаточных и оптических характеристик приведены в табл. 2. Таблица 2. Методы измерения передаточных и оптических характеристик...
-
Измерения узнаваемости голоса диктора методом парных сравнений проводит бригада операторов в составе: пяти дикторов: трех мужчин и двух женщин (далее Д1,...
-
Важной областью применения ЦАП является синтез аналоговых сигналов необходимой формы. Аналоговые генераторы сигналов - синусоидальной, треугольной и...
-
Измерения проводятся бригадой операторов в составе: трех дикторов: двое мужчин и одна женщина (далее Д1, Д2 и Д3); трех аудиторов: двое женщин и мужчина...
-
Выбор типа источника излучения и фотоприемника, их параметры Выбор типа источника излучения. Общие требования к источникам излучения ВОСП следующие: л...
-
Частота генератора тактовых импульсов, Гц....190 Счет ведется от числа....9 Шаг...............................1 Число состояний системы............8...
-
Геометрические критерии устойчивости - Критерии устойчивости линейных систем
Требование, чтобы передаточная функция Не имела полюсов в правой полуплоскости р = i, т. е. в области, ограниченной полуплоскостью бесконечно большого...
-
Метод обратного преобразования - Структурные методы повышения точности средств измерения
Этот метод применяется при автоматической коррекции погрешности средств измерений. Для реализации этого метода используется обратный преобразователь,...
-
ОПРЕДЕЛЕНИЯ НЕКОТОРЫХ ПАРАМЕТРОВ ИНТЕГРАЛЬНЫХ МИКРОСХЕМ - Цифровые устройства и микропроцессоры
Ниже приведены некоторые параметры в отечественном по ГОСТ 19480-89 и международном обозначении. Tзд. р.1,0 / tPHL - время задержки распространения при...
-
Если выходное сопротивление меньше волнового сопротивления, то согласование сводится к установке последовательного резистора R C на выход микросхемы....
-
К числу основных операций выполняемых при поверке гетеродинных анализаторов спектра (АС), относят определение следующих технических характеристик:...
Критерии согласия - Измерения параметров сигнала