Оценка параметров многомерной функции распределения - Измерения параметров сигнала
Параметр амплитуда сигнал
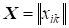
6.1. Обобщение основных определений на многомерные распределения. До сих пор мы изучали теорию оценок параметров или самих распределений одной случайной величины. Практический интерес представляют также оценки многомерных распределений или их параметров для совокупности зависимых случайных величин. В параметрической теории вид многомерной функции распределения этой совокупности известен, и оцениваются лишь неизвестные параметры, в непараметрической теории оценке подлежит сама функция распределения. В любом случае основанием для статистических выводов служит выборка из многомерного распределения. В отличие от одномерного случая, элементами такой (размера n) выборки служат не единичные измерения (числа), а N чисел. Тогда результаты измерений представляют собой прямоугольную матрицу размером (пример: отсчеты сигналов на выходах антенной решетки в разные моменты времени) . Функция правдоподобия выборки из N-мерного распределения представляет собой функцию n векторных аргументов. Параметрами этой функции представляют матрицы (или векторы), элементами которых являются неизвестные параметры многомерного распределения совокупности случайных величин. В частном случае для независимых элементов многомерной выборки функция правдоподобия
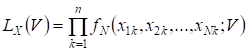
,
Где - плотность вероятности совокупности случайных величин.
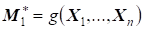
По выборке Х определяются S выборочных матриц (или векторов), зависящих от выборочных векторов, , I = 1,..., S, в предположении, что параметры плотности вероятности фиксированы. Эти выборочные матрицы (или векторы) представляют условные оценки матриц (или векторов), элементами которых являются неизвестные параметры.
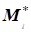
Каждая из условных оценок называется состоятельной, если при она сходится к. Оценка называется несмещенной, если для любого N ее среднее значение по совокупности векторных выборок равно. При этом следует иметь в виду, что под средним значением случайной матрицы (вектора) понимают матрицу (вектор), элементы которой равны средним значениям элементов случайной матрицы (вектора). Таким же образом обобщается понятие и совместно достаточных оценок. Для этого скалярные аргументы заменяются векторными.
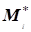
Оценки максимального правдоподобия получаются из системы уравнений
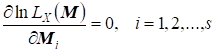
.
6.2. Оценки векторов средних и корреляционной матрицы многомерного нормального распределения. Проиллюстрируем указанные обобщения на примере N-мерного нормального распределения. Запишем плотность вероятности этого распределения в векторной форме:
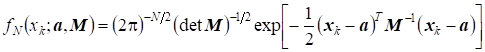
,
Где A - вектор средних значений; M - корреляционная матрица.
Пусть - независимые выборочные N-мерные векторы из нормального распределения. Функция правдоподобия выборки равна произведению N-мерных нормальных плотностей вероятностей:
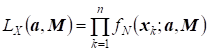
=
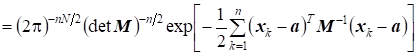
.
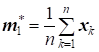
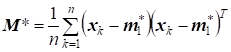
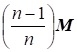
Введем вектор выборочных средних значений и выборочную корреляционную матрицу. Можно доказать, что оценка вектора математических ожиданий является несмещенной, в то время как оценка корреляционной матрицы смещенная, так как ее математическое ожидание равно. Поэтому несмещенной оценкой корреляционной матрицы M является величина.
Похожие статьи
-
Оценка неэнергетических параметров - Измерения параметров сигнала
Сигнал зависит от какого-либо неэнергетического параметра А , которым может быть задержка сигнала или смещение частоты (эффект Доплера в радиолокации)....
-
Методы получения оценок параметров - Измерения параметров сигнала
Многие важные задачи обработки сигналов сводятся к получению статистических выводов относительно всех или некоторых неизвестных параметров сигналов. При...
-
Критерии согласия - Измерения параметров сигнала
В предыдущих случаях при синтезе алгоритмов оценок параметров, алгоритмов обнаружения или различения сигналов предполагалось наличие априорной информации...
-
Интервальные оценки параметров сигналов - Измерения параметров сигнала
Как известно, точечные оценки параметров сигналов не позволяют оценить степень близости полученной оценки к истинному значению оцениваемого параметра....
-
Оптимальная оценка амплитуды сигнала - Измерения параметров сигнала
Представим сигнал в таком виде: , Где А - оцениваемая амплитуда; C ( T ) - сигнал с единичной амплитудой. Тогда выборка содержит два слагаемых: , Где, в...
-
1) Зафиксируем переход с черного поля на белое поле (или наоборот), см. рис.15 Рис. 15 2) Измерим амплитуду шума на черном поле, см. рис.16 (в данном...
-
Оценка частоты гармонических сигналов на основе анализа амплитудно-частотной характеристики процесса
Оценка частоты гармонических сигналов на основе анализа амплитудно-частотной характеристики процесса Бордюков Антон Геннадьевич, Аспирант...
-
Измерения узнаваемости голоса диктора методом парных сравнений проводит бригада операторов в составе: пяти дикторов: трех мужчин и двух женщин (далее Д1,...
-
Измерения проводятся бригадой операторов в составе: трех дикторов: двое мужчин и одна женщина (далее Д1, Д2 и Д3); трех аудиторов: двое женщин и мужчина...
-
Совместные распределения СП, Стационарность и эргодичность СП - Случайные процессы
Рассмотрим два случайных процесса и. Совместная функция распределения - го порядка: Совместная плотность вероятностей - го порядка: . Если для любых N, m...
-
Использование тестовых сигналов - Структурные методы повышения точности средств измерения
Тестовые методы повышения точности измерений применяются в различных измерительных системах для измерений как электрических, так и неэлектрических...
-
Определение чувствительности производится с помощью измерительного генератора, уровень входного сигнала которого или нормирован с допускаемой для поверки...
-
На втором этапе измерений речи артикуляционным методом проводится цикл измерений. Цикл измерений включает в себя результат приема всех аудиторов от всех...
-
Параметры входного сигнала (воздействия) u1(t) представлены в таблице 1.2 Таблица 1.2 - Параметры воздействия A 3 1 3 5 Значения A - в вольтах (В), т. к....
-
Алгоритм коррекции допусков на технические параметры авиационных радиоэлектронных комплексов
В работе осуждаются особенности исследований статистической зависимости между контролируемыми параметрами авиационных радиоэлектронных комплексов (РЭК)....
-
Сами элементы, на которых строятся активные фильтры, подвержены изменениям вследствие перемен окружающей среды (например, температуры и влажности) и...
-
Данная методика расчета основана на методе динамики моментов, базирующегося на тех же исходных линейных дифференциальных уравнениях теории непрерывных...
-
Рисунок 3.2 - Детерминированные сигналы Сигналы подразделяются на непрерывные (аналоговые) и прерывистые (дискретные). Сигналы - аналоговые, они...
-
Логистические затраты - это совокупность затрат на управление движением материальных потоков по всей логистической системе организации - от поставщиков...
-
Выбор рабочей длины волны Форма и длительность оптических импульсов. Оптические импульсы характеризуются зависимостью: P(t)=P0F(t) Длительность импульсов...
-
Оценка качества восстановленного речевого сигнала. - Фильтрация зашумленного речевого сигнала
Оценка качества речевого сигнала является важной задачей. Отношение сигнал/шум ( ОСШ ), являющееся одной из наиболее распространенных объективных мер для...
-
Динамические параметры ЦАП определяются по изменению выходного сигнала при скачкообразном изменении входного кода, обычно от величины "все нули" до "все...
-
При последовательном возрастании значений входного цифрового сигнала D(t) от 0 до 2N-1 через единицу младшего разряда (ЕМР) выходной сигнал UВых(t)...
-
Данные передача сигнал сообщение Для обеспечения заданной достоверности при передаче данных применяют обратные связи и помехоустойчивое кодирование,...
-
Объем работ по ЕОс, ЕОт, ТО-1, ТО-2 за год определяется произведением числа ТО на нормативное (скорректированное) значение трудоемкости данного вида ТО:...
-
N - число попаданий за четыре часа, TОб - время оборота подвижной единицы, ч, TОбср-среднее время оборота за час, ч. Таблица 10 Среднее время оборота...
-
Характеристика логистической инфраструктуры ООО "Мебельная компания ЛЕРОМ" ООО "Мебельная компания ЛЕРОМ" - российское предприятие, созданное в г. Пенза...
-
Накопленный опыт показывает, что попытка оценить степень удовлетворения потребностей народного хозяйства в перевозках грузов либо натуральными, либо...
-
В настоящей главе анализируются особенности методов, основанных на вычитании амплитудных спектров, для очистки речевых сигналов от стационарных и...
-
Предположим, что напряжение на входе детектора равно 150 мВ. Требуемый коэффициент усиления линейного тракта определяется как: (10) Реальный коэффициент...
-
Механические параметры оптических волокон - Параметры оптических волокон
К механическим параметрам ОВ относятся: * прочность волокна; * динамическая прочность на разрыв; * параметр нагрузки разрушения; * стойкость к изгибам; *...
-
Показатели разгона автомобиля представляют собой графики ускорений, времени и пути разгона в функции скорости. Ускорение j для разных передач и скоростей...
-
1. Шаг коррекции ( Дц ) - смещение фазы ТИ в долях единичного интервала ( Ф 0 ) на выходе делителя частоты (ДЧ) при добавлении или вычитании одного...
-
Обработка результатов прямого измерения - Измерение объективных характеристик видеооборудования
При проведении измерений хорошим тоном считается указание погрешности измерений (поскольку мы не можем измерять с абсолютной точностью величины) и...
-
1. Шаг коррекции (Дц) - смещение фазы ТИ в долях единичного интервала (ф0) на выходе делителя частоты (ДЧ) при добавлении или вычитании одного...
-
Представим спектральную плотность средней мощности отрезка (длительностью T ) вещественного стационарного случайного процесса в форме: , Где _ функция,...
-
МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ, ТАБЛИЦА КАРНО - Цифровые устройства и микропроцессоры
Полученные по формуле СДНФ (12) выражение может быть преобразовано (не всегда) к виду, имеющему меньшее число переменных и операций по сравнению с...
-
Графики переходных функций объекта и замкнутой системы
Контрольная работа по дисциплине: "Системы автоматического управления" Цель работы. Построить графики переходных функций объекта и замкнутой системы. По...
-
Цель: рассчитать геометрические параметры элементов печатного монтажа. Рассмотреть минимальные расстояния между элементами печатного рисунка...
-
Рассмотрим несколько конкретных примеров измерения параметров фильтра в полосных и гомоморфных вокодерах, а также в вокодерах с линейным предсказанием...
Оценка параметров многомерной функции распределения - Измерения параметров сигнала