Дискретне вейвлет-перетворення та часові ряди - Вейвлет-аналіз як особливий тип лінійного перетворення сигналів та фізичних даних
Напрямки їх використання для аналізу часових рядів, обробки сигналів та зображень, кодування інформації тощо.
Вейвлет-перетворення звичайно поділяють на дискретне вейвлет-перетворення (DWT) та неперервне вейвлет-перетворення (CWT).
В принципі, при обробці даних на ПК може виконуватися дискретизирован версія безперервного вейвлет-перетворення із завданням дискретних значень параметрів (a, b) вейвлетів з довільним кроком Da--і--Db. У результаті виходить надмірна кількість коефіцієнтів, що набагато перевершує число відліків вихідного сигналу, яке не потрібно для реконструкції сигналів. Дискретне вейвлет-перетворення (ДВП) забезпечує достатньо інформації, як для аналізу сигналу, так і для його синтезу, будучи разом з тим економним за кількістю операцій і по необхідної пам'яті. ДВП оперує з дискретними значеннями параметрів а і б, які задаються, як правило, у вигляді степеневих функцій:
--a--=--ао-m,--b--=--k-ао-m,--ao-->--1,--m,--k----I,
Де I - простір цілих чисел {-, }, m - параметр масштабу, k - параметр зсуву. Базис простору L2(R) в дискретному поданні:
ymk(t)--=--|ао|m/2y(аоmt-k),--m,k----I,--y(t)----L2(R)
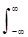
Вейвлет-коэффіцієнти прямого перетворення: Cmk--=s(t)--ymk(t) dt. Значення''може бути довільним, але зазвичай приймається рівним 2, при цьому перетворення називається діадного вейвлет-перетворенням. Для діадного перетворення розроблено швидкий алгоритм обчислень, аналогічний швидкому перетворенню Фур'є, що зумовило його широке використання при аналізі масивів цифрових даних. Зворотне дискретне перетворення для безперервних сигналів при нормованому ортогональному вейвлетного базисі простору:
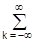
s(t)--=----Cmk--ymk(t).
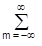
Число використаних вейвлетів щодо масштабного коефіцієнту м задає рівень декомпозиції сигналу, при цьому за нульовий рівень (m = 0) зазвичай приймається рівень максимального тимчасового дозволу сигналу, тобто сам сигнал, а наступні рівні (m <0) утворюють спадаюче вейвлет-дерево. У програмному забезпеченні обчислень для виключення використання негативної нумерації по м знак 'мінус' зазвичай переноситься безпосередньо, тобто використовується наступне подання базисних функцій:
ymk(t)--=--|ао|-m/2y(ао-mt-k),--m,k----I,--y(t)----L2(R)
Стійкість дискретного базису визначається наступним чином.
Функція y(t)--L2(R) називається R-функцією, якщо базис на її основі по являється базисом Рісса (Riesz). Для базиса Рісса існують значення А і В, 0 < A ? B < , для яких виконується відношення:
A||Cmk||2--d--||----Cmk--ymk(t)||2--d--B||Cmk||2,
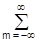
Якщо енергія ряду CMk кінечна. При цьому для будь-якої R-функції існує базис--y#mk(t), який ортогональний базису y#mk(t). його називають ортогональним "двійником" базиса--y#mk(t), таким, что
ymk(t),--y#nl(t)--=--dmn-dkl.
Якщо A = B = 1 і аО = 2, то сімейство базисних функцій {ymk(t) } є ортонормированном базисом і можливо повне відновлення вихідного сигналу, при цьому ymk(t)--a--y#mk(t) і для реконструкції сигналів використовується формула. Якщо y(t) не ортогональний вейвлет, але має "двійника", то на базі "двійника" обчислюється сімейство ymk(t), яке і використовується при зворотному перетворенні замість ymk(t), при цьому точну відновлення вихідного сигналу не гарантовано, але воно буде близько до нього в середньоквадратичних сенсі. Як і для безперервного вейвлет-перетворення, зворотне дискретне перетворення не може виконати відновлення нецентрірованних сигналів в силу нульового першого моменту вейвлетного функцій і, відповідно, центрування значення вейвлет-коефіцієнтів ЦМК при прямому вейвлет-перетворенні. Тому при обробці числових масивів даних дискретні вейвлети використовуються, як правило, в парі з пов'язаними з ними дискретними скейлинг-функціями. Скейлін-функції мають з вейвлетами загальну область завдання і певне співвідношення між значеннями, але перший момент скейлін-функцій по області визначення дорівнює 1. Якщо вейвлети розглядати, як аналоги смугових фільтрів сигналу, в основному, високочастотних при виділенні локальних особливостей в сигналі, то скейлін-функції вейвлетів є аналоги низькочастотних фільтрів, якими з сигналу виділяються в окремий масив складові, які не пройшли вейвлетного фільтрацію. Так, наприклад, породжує скейлинг-функція вейвлета Хаара задається наступним виразом:
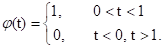
При позначенні скейлинг-функцій індексом jMk(t) аналітика скейлін-функцій повторює висловлювання (1.2.6-1.2.7) і утворює додатковий базис простору L2 (R). Сума вейвлет-коефіцієнтів і скейлинг-коефіцієнтів розкладання сигналів відповідно дає можливість виконувати точну реконструкцію сигналів, при цьому замість (1.2.8) використовується наступний вираз зворотного вейвлет-перетворення:
s(t)--=Сak--jk(t)--+--Сdmk--ymk(t),--(1.2.9)
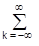
Де CaK - скейлін-коефіцієнти, які зазвичай називають коефіцієнтами апроксимації сигналу, CdMk - вейвлет-коефіцієнти або коефіцієнти деталізації. Більш докладно використання скейлинг-функцій буде розглянуто в темі вейвлетного кратномасштабного аналізу.
Реальні сигнали, як правило, кінцеві і належать простору L2 (R). Частотний спектр сигналів обернено пропорційний їх тривалості. Відповідно, досить точний низькочастотний аналіз сигналу повинен проводитися на великих інтервалах його завдання, а високочастотний - на малих. Якщо частотний склад сигналу зазнає істотні зміни на інтервалі його завдання, то перетворення Фур'є дає тільки усереднені дані частотного складу сигналу з постійним частотним дозволом. Певна частотно-тимчасова локалізація аналізу створюється застосуванням віконного перетворення Фур'є, що дає сімейства частотних спектрів, локалізованих у часі, але в межах постійної ширини вікна віконної функції, а, отже, також з постійним значенням і частотного, і тимчасового дозволу.
На відміну від віконного перетворення Фур'є, вейвлет-перетворення, при аналогічних дискретних значеннях зрушень b, дає сімейства спектрів масштабних коефіцієнтів а стиснення-розтягування
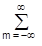
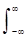
С(a,b)--=s(t)--|а|-1/2yо[(t-b)/а]dt.
Якщо вважати, що кожен вейвлет має певну "ширину" свого тимчасового вікна, якому відповідає певна "середня" частота спектрального образу вейвлета, зворотній його масштабного коефіцієнту а, то сімейства масштабних коефіцієнтів вейвлет-перетворення можна вважати аналогічними домами частотних спектрів віконного перетворення Фур'є, але з одним принциповим відзнакою. Масштабні коефіцієнти змінюють "ширину" вейвлетів і, відповідно, "середню" частоту їх фур'є-образів, а, отже, кожній частоті відповідає своя тривалість тимчасового вікна аналізу, і навпаки. Так малі значення параметра а, що характеризують швидкі складові в сигналах, відповідають високим частотам, а великі значення - низьким частотам. За рахунок зміни масштабу вейвлети здатні виявляти відмінності на різних частотах, а за рахунок зсуву (параметр b) проаналізувати властивості сигналу в різних точках на всьому досліджуваному часовому інтервалі. Великорозмірними тимчасове вікно вейвлет-перетворення адаптовано для оптимального виявлення і низькочастотних, і високочастотних характеристики сигналів.
Для довільної віконної функції z(t) L2(R) її центр і радіус визначаються формулами:
- to--=t--|z(t)|2--dt, Dz--=----
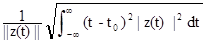
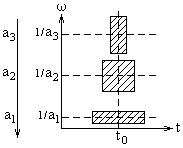
Якщо з цих функцій визначити центри і радіуси вейвлетів та їх фур'є-образів, то тимчасова локалізація відбувається з центрами вікон b+atO шириною winT = 2a???t???а частотна - з центрами ?О/а, і з шириною вікна win? = 2???????/а. При цьому значення відношення середньої частоти до ширини вікна не залежить від місця розташування центральної частоти. Частотно-часове вікно winT-win? = 4???t??????Звужується при високій центральній частоті, і розширюється при низькою. Схематичне зображення частотно-часових вікон перетворення наведено на рис. 1.2.4. Таким чином, на високих частотах краще дозвіл за часом, а на низьких - по частоті. Для високочастотної компоненти сигналу ми можемо точніше вказати її тимчасову позицію, а для низькочастотної - її значення частоти.
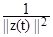
Зміна частотно-часового вікна вейвлета визначає кут впливу значень функції в довільних точках tI на значення коефіцієнтів С(а, b). І навпаки, кут впливу з точки С(aI,bI) на вісь т визначає інтервал значень функції, які беруть участь в обчисленні цього коефіцієнта С(aI,bI) - область достовірності. Схематично це показано на рис.
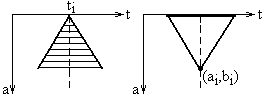
З кутку впливу наочно видно, що високочастотна (дрібномасштабні) інформація обчислюється на основі малих інтервалів сигналів, а низькочастотна - на основі великих. Оскільки аналізовані сигнали завжди кінцеві, то при обчисленні коефіцієнтів на кордонах завдання сигналу область достовірності виходить за межі сигналу, і для зменшення похибки обчислень сигнал доповнюється завданням початкових і кінцевих умов. Дискретне вейвлет-перетворення (DWT) звичайно використовується для кодування сигналів, у той час як CWT для аналізу сигналів. Саме тому, DWT широко застосовується в інженерній справі і комп'ютерних науках, а CWT у наукових дослідженнях фізичних процесів. Вейвлет-перетворення в даний час взяті на озброєння для величезної кількості різнопланових застосувань, нерідко заміняючи звичайне перетворення Фур'є у багатьох прикладних задачах. Ця зміна парадигми спостерігається в багатьох областях фізики, включаючи молекулярну динаміку, астрофізику, квантовій механіці, геофізиці, оптиці, механіці рідини та у багатьох інших областях, включаючи обробку зображень, аналізу кров'яного тиску, пульсу та ЕКГ, аналіз ДНК, дослідження білків, вивчення клімату, загальну обробку сигналів, розпізнавання мови, комп'ютерну графіку і мультифрактальний аналіз. Таке широке використання вейвлет-перетворень забезпечується можливістю побудувати на їх основі методи, що потребуватимуть O(N) операцій, на противагу методів Фур'є-перетворень, де кількість операцій не менша за O(NlogN).
Похожие статьи
-
Вейвлет (wavelet, вейвлет-перетворення, хвильки, хвилькові перетворення). Усі вейвлет-перетворення розглядають функцію (взяту як функцією від часу) у...
-
У практиці передачі інформації часто потрібно представити сигнал у вигляді сукупності його послідовних наближень. Наприклад, при перегляді і передачі...
-
Вейвлети - це математичні функції, що дозволяють аналізувати різні частотні компоненти даних. Вейвлети володіють істотними перевагами в порівнянні з...
-
Висновок - Вейвлет-аналіз як особливий тип лінійного перетворення сигналів та фізичних даних
Вейвлет перетворення градієнтський поток Вейвлет-аналіз є особливим типом лінійного перетворення сигналів та фізичних даних Останнім часом виник і...
-
Вступ - Вейвлет-аналіз як особливий тип лінійного перетворення сигналів та фізичних даних
Термін "вейвлет" (wavelet) в перекладі з англійської означає "маленька (коротка) хвиля". Вейвлети - це узагальнена назва сімейства математичних функцій...
-
Джерела інформації мають фізичну природу, відрізняються по виду формованих повідомлень, енергетичній активності, імовірнісним характеристикам. Для...
-
6 Застосування дискретного перетворення Фур'є - Розробка процесора ШПФ
1. Цифровий спектральний аналіз - Аналізатори спектра - Обробка мови - Обробка зображень - Розпізнавання образів 2. Проектування фільтрів - Обчислення...
-
Особливості обробки сигналів в системі мобільного зв'язку з ЦДУ Як відомо, ємність СМЗ обумовлена кількістю абонентів, які вона може обслужити, є дуже...
-
Этап 1. Пусть имеется исходный зашумленный сигнал, состоящий из чистого речевого сигнала и некоррелированного аддитивного шума, который определяется...
-
Вихідні дані: адреси блоку - 160636, 160640; напруга живлення логічного блоку - 5В; напруга живлення зовнішніх пристроїв - 24 В; індикація станів схеми;...
-
Швидке перетворення Фур'є - Розробка процесора ШПФ
Вихідними даними для ШПФ є елементи обмеженої послідовності x(n), де n=0,1,.. N-1. Відповідно дискретне перетворення Фур'є має вид: (1) (2) Де -...
-
Оценка частоты гармонических сигналов на основе анализа амплитудно-частотной характеристики процесса
Оценка частоты гармонических сигналов на основе анализа амплитудно-частотной характеристики процесса Бордюков Антон Геннадьевич, Аспирант...
-
В настоящей главе анализируются особенности, свойства и характеристики речевых сигналов. Виды шумов акустических помех и искажений, а так же особенности...
-
Построим сигнал на выходе регенератора для заданной кодовой последовательности символов для линейного кода МЧПИ. Построение глаз - диаграммы на выходе...
-
Математичні моделі сигналів - Математичний опис джерел інформації, сигналів, завад і каналів зв'язку
Відеосигнали u(t), розглянуті в 1, не є основними переносниками інформації. Вони переносять її по внутрішніх ланцюгах. Переносниками інформації на далекі...
-
Вид принимаемого сигнала - ЖК-телевизоры
Полный телевизионный сигнал включает в себя широкий спектр частот, цветовых сигналов с частотой подмодуляции внутри яркостного канала модулированного по...
-
Оценка неэнергетических параметров - Измерения параметров сигнала
Сигнал зависит от какого-либо неэнергетического параметра А , которым может быть задержка сигнала или смещение частоты (эффект Доплера в радиолокации)....
-
Первичные сигналы электросвязи и их характеристики. - Основы техники связи
Электрический сигнал, получаемый на выходе преобразователя сообщения (см. рисунок 2.1, глава 2), называется первичным сигналом электросвязи. Параметр...
-
Для налаштування антени булоб добре знати потужність сигналу на виході конвертора. Це можливо зробити знаючи ЕІВП супутника (карти зон покриття тим чи...
-
Способи модуляції - Захист інформації від витоку з телефонної мережі зв'язку
У модемах для телефонних каналів, як правило, використаються три види модуляції: частотна, відносна фазова (фазоразностна) і квадратурна амплітудна...
-
Локализация сигналов методом фильтрации и заземление технических средств
Фильтрация Одним из методов локализации опасных сигналов, циркулирующих в технических средствах и системах обработки информации, является фильтрация. В...
-
Вимір М періодів вхідного сигналу - Вимірювач частоти
Як видно, розглянуті перші два способи виміру частоти проходження імпульсів не дають можливості вимірити параметри вхідного сигналу з достатньою точністю...
-
&;nbsp;Искусственные линии задержки. - Оcновы радиоэлектроники
На практике чаще всего в качестве ЛЗ применяют искусственные линии с сосредоточенными параметрами. Такие линии позволяют получить заданное время задержки...
-
Пристрої виміру частоти є одним з типів пристроїв з використанням мікроконтроллерів. В основі даних пристроїв обов'язковим елементом є мікроконтролер, що...
-
Во временной области Класс методов цифровой обработки зашумленных речевых сигналов, который основан на построении математических моделей речевых сигналов...
-
Для відкритих трас множник послаблення може бути розрахований за наступною формулою: - модуль коефіцієнта відбиття, величина якого залежить від характеру...
-
Для выявления основных закономерностей рассмотрим реакцию НЭ на воздействие двух гармонических сигналов. Такое воздействие принято называть...
-
Як правило, на будинках в садоводствах, що знаходяться на відстані не більше 20 км. від ТЦ і активних ретрансляторів, використовуються однопрограммниє і...
-
Архітектура PIC контролерів - Структурні особливості сучасних мікропроцесорних систем
PIC16fXX - це 8-розрядні FLASH CMOS мікроконтролери з RISC архітектурою, вироблені фірмою Microchip Technology. Це сімейство мікроконтролерів...
-
Определение чувствительности производится с помощью измерительного генератора, уровень входного сигнала которого или нормирован с допускаемой для поверки...
-
В процессе квантования по уровню значение каждого АИМ-отсчета заменяется ближайшим разрешенным значением. Характеристиками квантующего устройства...
-
В процессе формирования АИМ сигнала осуществляется дискретизация непрерывного (аналогового) сигнала во времени в соответствии с известной Теоремой...
-
При розробці і настроюванні систем автоматичного керування важливо встановити вплив окремих параметрів на їх стійкість. Для визначення областей...
-
Оптимизация по критерию максимума отношения сигнал/шум - Оптимальные линейные системы
Рассмотрим, аналогично 4.1.1, обработку сигнала на фоне "белого шума" , по-прежнему используя в качестве критерия оптимальности критерий максимума...
-
При воздействии на вход типового каскада радиоканала полезного сигнала и белого шума главной задачей является оценка помехоустойчивости системы. В нашем...
-
Энергетический спектр шума на выходе УНЧ: (4.1) Где W3(щ) - энергетический спектр шума на выходе АК. Рисунок 4.1 Энергетический спектр шума на выходе УНЧ...
-
Обзор методов построения аналогичных устройств - Проектирование усилителей электрических сигналов
Усилителями постоянного тока (УПТ) называются устройства, предназначенные для усиления медленно изменяющихся сигналов вплоть до нулевой частоты. На рис....
-
Оптимальная оценка амплитуды сигнала - Измерения параметров сигнала
Представим сигнал в таком виде: , Где А - оцениваемая амплитуда; C ( T ) - сигнал с единичной амплитудой. Тогда выборка содержит два слагаемых: , Где, в...
-
Цифровий потік ТМ програми включає в себе елементарний потік відеоданних, звукоданних, даних додаткової інформації (даних користувача), що утворяться...
-
Мета роботи: набуття практичних навичок щодо використання методів статистичних рішень в задачах діагностування авіаційної техніки. Стислі теоретичні...
Дискретне вейвлет-перетворення та часові ряди - Вейвлет-аналіз як особливий тип лінійного перетворення сигналів та фізичних даних