Частотний підхід та швидке вейвлет-перетворення - Вейвлет-аналіз як особливий тип лінійного перетворення сигналів та фізичних даних
Вейвлет (wavelet, вейвлет-перетворення, хвильки, хвилькові перетворення). Усі вейвлет-перетворення розглядають функцію (взяту як функцією від часу) у термінах коливань, локалізованих за часом (простором) і частотою. Локальність у просторі означає, що енергія хвильок (вейвлетів) сконцентрована на скінченному інтервалі, так звана функція на компактному носії. Частотна локалізація означає, що перетворення Фур'є хвилькі локалізоване. Частотна локалізація функції зводиться до понять гладкості та кількості зникаючих моментів.
Вейвлет-перетвореня сигналів є узагальненням спектрального аналізу, типовий представник якого - класичне перетворення Фур'є. Застосовувані для цієї мети базиси названі вейвлетами. Термін "вейвлет" пішов від англійського wavelet, що на українську мову переводиться як "коротка хвиля''. У математичній літературі поняття "вейвлет" позначають іноді словом "сплеск", що звужує саме поняття, тим більше, що вейвлети й призначені для аналізу сплесків - сигналів нестаціонарного характеру.
Введені порівняно недавно, в 80-х роках, вони в наступні роки одержали швидкий теоретичний розвиток і широке застосування в різних областях обробки сигналів і зображень. На відміну від традиційного перетворення Фур'є, вейвлет-перетворення забезпечує двовимірне подання досліджуваного сигналу в частотній області в площині частота-положення. Аналогом частоти при цьому є масштаб аргументу базисної функції (найчастіше часу), а положення характеризується її зрушенням. Це дозволяє розділити великі й дрібні деталі сигналів, одночасно локалізуючи їх на тимчасовій шкалі. Іншими словами вейвлет-аналіз можна охарактеризувати як локалізований спектральний аналіз або - спектральний аналіз локальних збурювань. Апаратурним аналогом одного з видів вейвлет-аналіза є багато канальна смугова фільтрація сигналу при постійному відношенні ширини смуги фільтра до центральної частоти.
Вейвлет-аналіз розроблений для рішення завдань, які виявилися занадто складними для традиційного аналізу Фур'є. Перетворення Фур'є представляє сигнал, заданий у тимчасовій області, у вигляді розкладання по ортогональних базисних функціях (синусам і косинусам) з виділенням частотних компонентів. Недолік перетворення Фур'є полягає в тому, що частотні компоненти не можуть бути локалізовані в часі, його застосовують тільки в аналізі стаціонарних сигналів, у той час як багато сигналів мають складні частотно-часові характеристики. Як правило, такі сигнали складаються із близьких за часом, коротких високочастотних компонентів і довгих, близьких по частоті низькочастотних компонентів. Для аналізу таких сигналів необхідний метод, здатний забезпечити одночасний дозвіл як по частоті, так і за часом. Перше необхідно для локалізації низькочастотних складових, друге - для виділення компонентів високої частоти. Існує два підходи до аналізу нестаціонарних сигналів такого типу. Перший заснований на локальному перетворенні Фур'є. Прямуючи цим шляхом, нестаціонарний сигнал зводиться до стаціонарного шляхом його попереднього розбиття на сегменти (фрейми), статистика яких не змінюється з часом. Другий підхід полягає у використанні вейвлет-перетворення.
Всім відомо, що будь-який сигнал можна розкласти в суму гармонік (синусоїд) різної частоти. Але синусоїдальні хвилі нескінченні, і не дуже добре відслідковують зміни сигналу в часі. Щоб вловити ці зміни, замість нескінченних хвиль можна взяти зовсім однакові, але розподілені за часом короткі "сплески". Однак, як виявилося, цього недостатньо, треба додати ще їхні стислі копії. От тепер сигнал можна розкласти на суму таких сплесків різного розміру й місця розташування. Коефіцієнти розкладу, які несуть інформацію про еволюції сигналу, залежать від вибору початкового сплеску. Для кожного прикладного завдання можна підібрати найбільш пристосований (саме для неї) сплеск, що і називається вейвлетом. Математична сторона вейвлет-аналіза - річ досить тонка, хоча й достатньо наочна. Як правило, вейвлет-перетворення (WT) поділяють на дискретне (DWT) і безперервне (CWT).
DWT - використовується для перетворень і кодування сигналів, CWT - для аналізу сигналів. Вейвлет-перетворення в даний час приймаються на озброєння для величезної кількості різноманітних застосувань, нерідко заміняючи звичайне перетворення Фур'є. Це спостерігається в багатьох областях, включаючи молекулярну динаміку, квантову механіку, астрофізику, геофізику, оптику, комп'ютерну графіку і обробку зображень, аналіз ДНК, дослідження білків, дослідження клімату, загальну обробку сигналів і розпізнавання мови.
Одна з головних і особливо плідних ідей вейвлетного подання сигналів на різних рівнях декомпозиції (розкладання) полягає в поділі функцій наближення до сигналу на дві групи: апроксимуючу - грубу, з досить повільною тимчасової динамікою змін, і деталізує - з локальної та швидкою динамікою змін на тлі плавною динаміки, з подальшим їх подрібненням і деталізацією на інших рівнях декомпозиції сигналів. Це можливо як в тимчасовій, так і в частотній областях подання сигналів вейвлетами.
В основі вейвлет-перетворень, в загальному випадку, лежить використання двох безперервних, взаємозалежних і інтегрованих з незалежної змінної функцій:
- * Вейвлет-функції (t), як psi-функції часу з нульовим значенням інтеграла і частотним фур'є-образом (?). Цією функцією, яку зазвичай і називають вейвлетом, виділяються локальні особливості сигналу. Як вейвлетів зазвичай вибираються функції, добре локалізовані і в тимчасовій, і в частотній області. Приклад тимчасового і частотного образу функції наведено на рис. 1.2.1. * масштабуючий функції (t), як тимчасової скейлинг-функції phi з одиничним значенням інтеграла, якій виконується грубе наближення (апроксимація) сигналу.
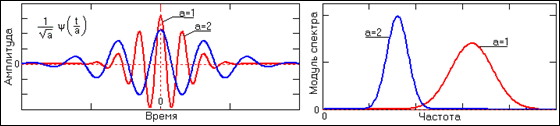
Рис. 1.2.1. Вейвлетні функції в двох масштабах.
Phi-функції властиві не всім, а, як правило, тільки ортогональним вейвлета. Вони необхідні для перетворення нецентрірованних і досить протяжних сигналів при роздільному аналізі низькочастотних і високочастотних складових. Роль і використання фі-функції розглянемо трохи пізніше.
Безперервне вейвлет-перетворення (НВП, CWT-Безперервне вейвлет-перетворення). Припустимо, що ми маємо функції s(t) з кінцевою енергією в просторі L2(R), визначені на всій дійсній осі R(-, ). Для фінітних сигналів з кінцевою енергією середні значення сигналів повинні прагнути до нуля на ± .
Безперервним вейвлет-перетворенням (або вейвлетного чином) функції s(t) L2(R) називають функцію двох змінних:
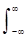
С(a,b)--=--s(t),--y(a,b,t)--=--s(t)--y(а,b,t)--dt,--a,--b----R,--a--`--_,--
Де вейвлети y(a,b,t)----yab(t) - масштабовані і зсунуті копії породжує вейвлета y(t)----L2(R), сукупність яких створює базис простору L2(R).
Породжують функціями можуть бути самі різні функції з компактним носієм - обмежені за часом і місцем розташування на тимчасової осі, і мають спектральний образ, локалізований на частотної осі. Базис простору L2(R) доцільно конструювати з одного породжує функції, норма якої повинна дорівнювати 1. Для перекриття функцією вейвлета всій тимчасової осі простору використовується операція зсуву (зміщення з тимчасової осі): ?(b, t) = ?(t-b), де значення b для НВП є величиною безперервною. Для перекриття всього частотного діапазону простору L2(R) використовується операція тимчасового масштабування вейвлета з безперервним зміною незалежної змінної: y(a,t)--=--|а|-1/2y(t/а). На рис. 1.2.1. видно, що якщо часовий образ вейвлета буде розширюватися (зміною значення параметра 'а'), то його "середня частота" буде знижуватися, а частотний образ (частотна локалізація) переміщатися на більш низькі частоти. Таким чином, шляхом зсуву по незалежній змінній (t-b) вейвлет має можливість переміщатися по всій числовій осі довільного сигналу, а шляхом зміни масштабної змінної 'а' (у фіксованій точці (t-b) осі) "переглядати" частотний спектр сигналу за певним інтервалу околиць цієї точки.
З використанням цих операцій вейвлетного базис функціонального простору утворюється шляхом масштабних перетворень і зрушень породжує вейвлета --y(t):
y(a,b,t)--=--|а|-1/2y[(t-b)/а],--a,--b----R,--a--`--_,--y(t)----L2(R).--
Неважко переконатися, що норми вейвлетів y(a,b,t) рівні нормі y(t), що забезпечує нормувальні множник |а|-1/2. При нормуванні до 1 породжує вейвлета y(t)усі сімейство вейвлетів також буде нормованим. Якщо при цьому виконується вимога ортогональності функцій, то функції y(a,b,t) утворюють ортонормованій базис простору L2(R).
Похожие статьи
-
Напрямки їх використання для аналізу часових рядів, обробки сигналів та зображень, кодування інформації тощо. Вейвлет-перетворення звичайно поділяють на...
-
У практиці передачі інформації часто потрібно представити сигнал у вигляді сукупності його послідовних наближень. Наприклад, при перегляді і передачі...
-
Вейвлети - це математичні функції, що дозволяють аналізувати різні частотні компоненти даних. Вейвлети володіють істотними перевагами в порівнянні з...
-
Вступ - Вейвлет-аналіз як особливий тип лінійного перетворення сигналів та фізичних даних
Термін "вейвлет" (wavelet) в перекладі з англійської означає "маленька (коротка) хвиля". Вейвлети - це узагальнена назва сімейства математичних функцій...
-
Висновок - Вейвлет-аналіз як особливий тип лінійного перетворення сигналів та фізичних даних
Вейвлет перетворення градієнтський поток Вейвлет-аналіз є особливим типом лінійного перетворення сигналів та фізичних даних Останнім часом виник і...
-
Джерела інформації мають фізичну природу, відрізняються по виду формованих повідомлень, енергетичній активності, імовірнісним характеристикам. Для...
-
Швидке перетворення Фур'є - Розробка процесора ШПФ
Вихідними даними для ШПФ є елементи обмеженої послідовності x(n), де n=0,1,.. N-1. Відповідно дискретне перетворення Фур'є має вид: (1) (2) Де -...
-
В настоящей главе анализируются особенности, свойства и характеристики речевых сигналов. Виды шумов акустических помех и искажений, а так же особенности...
-
Для відкритих трас множник послаблення може бути розрахований за наступною формулою: - модуль коефіцієнта відбиття, величина якого залежить від характеру...
-
Локализация сигналов методом фильтрации и заземление технических средств
Фильтрация Одним из методов локализации опасных сигналов, циркулирующих в технических средствах и системах обработки информации, является фильтрация. В...
-
Пристрої виміру частоти є одним з типів пристроїв з використанням мікроконтроллерів. В основі даних пристроїв обов'язковим елементом є мікроконтролер, що...
-
Математичні моделі сигналів - Математичний опис джерел інформації, сигналів, завад і каналів зв'язку
Відеосигнали u(t), розглянуті в 1, не є основними переносниками інформації. Вони переносять її по внутрішніх ланцюгах. Переносниками інформації на далекі...
-
Для выявления основных закономерностей рассмотрим реакцию НЭ на воздействие двух гармонических сигналов. Такое воздействие принято называть...
-
Оценка частоты гармонических сигналов на основе анализа амплитудно-частотной характеристики процесса
Оценка частоты гармонических сигналов на основе анализа амплитудно-частотной характеристики процесса Бордюков Антон Геннадьевич, Аспирант...
-
6 Застосування дискретного перетворення Фур'є - Розробка процесора ШПФ
1. Цифровий спектральний аналіз - Аналізатори спектра - Обробка мови - Обробка зображень - Розпізнавання образів 2. Проектування фільтрів - Обчислення...
-
Вид принимаемого сигнала - ЖК-телевизоры
Полный телевизионный сигнал включает в себя широкий спектр частот, цветовых сигналов с частотой подмодуляции внутри яркостного канала модулированного по...
-
Особливості обробки сигналів в системі мобільного зв'язку з ЦДУ Як відомо, ємність СМЗ обумовлена кількістю абонентів, які вона може обслужити, є дуже...
-
Первичные сигналы электросвязи и их характеристики. - Основы техники связи
Электрический сигнал, получаемый на выходе преобразователя сообщения (см. рисунок 2.1, глава 2), называется первичным сигналом электросвязи. Параметр...
-
Для налаштування антени булоб добре знати потужність сигналу на виході конвертора. Це можливо зробити знаючи ЕІВП супутника (карти зон покриття тим чи...
-
Вимір М періодів вхідного сигналу - Вимірювач частоти
Як видно, розглянуті перші два способи виміру частоти проходження імпульсів не дають можливості вимірити параметри вхідного сигналу з достатньою точністю...
-
Этап 1. Пусть имеется исходный зашумленный сигнал, состоящий из чистого речевого сигнала и некоррелированного аддитивного шума, который определяется...
-
Типовые дискретные звенья - Теория дискретных систем
Сложную передаточную функцию дискретной системы удобно представлять в виде произведения передаточных функций типовых звеньев не выше второго порядка, как...
-
Мостовий генератор для УЗВ-п'єзовипромінювача - Аналітичний огляд генераторів коливань
В останні роки все частіше доводиться зіштовхуватися з ультразвуком - звуковими коливаннями, що мають частоту більшу, ніж здатна почути людина. У...
-
Способи модуляції - Захист інформації від витоку з телефонної мережі зв'язку
У модемах для телефонних каналів, як правило, використаються три види модуляції: частотна, відносна фазова (фазоразностна) і квадратурна амплітудна...
-
Зазвичай в РЛС сантиметрового діапазону у якості малошумлячого підсилювача МШП надвисоких частот НВЧ використовують тільки напівпровідниковий...
-
Мостовий метод вимірювання частоти - Вимірювання частоти
Цей метод оснований на використанні частотно залежних мостів змінного струму, які живляться напругою вимірюваної частоти. Найбільш поширеною мостовою...
-
&;nbsp;Искусственные линии задержки. - Оcновы радиоэлектроники
На практике чаще всего в качестве ЛЗ применяют искусственные линии с сосредоточенными параметрами. Такие линии позволяют получить заданное время задержки...
-
Для передачи по одному частотному каналу в GSM представляется цифровой поток (8 x 33.8Кбит/с)=270.4 Кбит/с. При этом ширина полосы канала 200кГц. Простые...
-
Будую діаграму рівнів (додаток 1). Сигнал Pпрд, передається в передавальну антену, при цьому послаблюється в фідерній лінії на 1дб, далі рівень сигналу...
-
К методам этого типа относятся, прежде всего, класс методов обработки зашумленных речевых сигналов, которые используют квазипериодичность речевого...
-
Только в том случае, когда в процессе преобразования применяются "искажающие" операции - изменение разрядности отсчета, частоты дискретизации,...
-
Кібернетичний підхід до поняття інформації - Теорія інформації як основа інформаційних технологій
Розглянемо підхід до поняття інформації з погляду кібернетики. Інформація відомості, які нас цікавлять. Інформація повідомлення, які володіють новизною...
-
В процессе квантования по уровню значение каждого АИМ-отсчета заменяется ближайшим разрешенным значением. Характеристиками квантующего устройства...
-
В процессе формирования АИМ сигнала осуществляется дискретизация непрерывного (аналогового) сигнала во времени в соответствии с известной Теоремой...
-
Построим сигнал на выходе регенератора для заданной кодовой последовательности символов для линейного кода МЧПИ. Построение глаз - диаграммы на выходе...
-
Энергетический спектр шума на выходе УНЧ: (4.1) Где W3(щ) - энергетический спектр шума на выходе АК. Рисунок 4.1 Энергетический спектр шума на выходе УНЧ...
-
Обзор методов построения аналогичных устройств - Проектирование усилителей электрических сигналов
Усилителями постоянного тока (УПТ) называются устройства, предназначенные для усиления медленно изменяющихся сигналов вплоть до нулевой частоты. На рис....
-
Оценка неэнергетических параметров - Измерения параметров сигнала
Сигнал зависит от какого-либо неэнергетического параметра А , которым может быть задержка сигнала или смещение частоты (эффект Доплера в радиолокации)....
-
Цифровий потік ТМ програми включає в себе елементарний потік відеоданних, звукоданних, даних додаткової інформації (даних користувача), що утворяться...
-
H2 = , Отсюда получим h = 1.79 Рассчитаем вероятность неправильного принятия решения в рассматриваемом приемнике (ДЧМ, КГ). Воспользуемся формулой...
Частотний підхід та швидке вейвлет-перетворення - Вейвлет-аналіз як особливий тип лінійного перетворення сигналів та фізичних даних