Гравитационная неустойчивость сред и пучков частиц - Гравитационные явления и гравитационная неустойчивость
В гравитирующих средах под влиянием гравитации могут образовываться структуры. Задачу звездообразования в нерелятивистском газе впервые рассмотрел английский астроном Джеймс Джинс [16] в 1902 г. Следуя Джинсу, рассмотрим газообразную среду, находящуюся в собственном гравитационном поле. Эта среда описывается уравнениями классической гидродинамики и уравнением Пуассона для классического гравитационного потенциала [17] .

, (8)

.
Здесь плотность вещества, давление, гидродинамическая скорость, оператор Лапласа.
Пусть, вследствие случайных причин, в этой среде возникнут малые возмущения гидродинамических и полевых параметров. Эти возмущения аналогичны звуку от упавшего камня, распространяющемуся в воде. Предположим, что основное состояние среды есть. Тогда полные гидродинамические величины есть:
(9)
Где
То есть все возмущенные величины являются одной из гармоник полного преобразования Фурье. Поэтому, использованный здесь метод называется также методом экспресс - анализа дифференциальных уравнений и является достаточно общим.
Подставляя (9) в (8), получим дисперсионное соотношение для волн в среде
(10)
Где

- скорость звука в среде.
Дисперсионное соотношение (10) описывает борьбу между силами гравитации, пропорциональными ньютоновской гравитационной константе G, и давлением p в среде. Свойства решений в (10) зависят от знака выражения в правой части. При фиксированных свойствах среды, т. е. при данных и существует критическое значение волнового вектора, определяемое условием

(11)
При (преобладание давления среды над силами гравитации) решение описывает распространение звуковых волн. При (гравитация преобладает над давлением) возмущения растут и, в конце концов образуют структуры в среде.
Если среда не является сплошной и состоит из отдельных частиц, она описывается не уравнениями (9), а кинетическими уравнениями. Пусть функция распределения в 6-мерном пространстве координат и импульсов. Уравнения движения частиц такой разреженной среды есть [18-20]

(12)
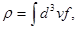
Пользуясь (12) , решим задачу Джинса о поведении кинетических частиц


(13)
Представим возмущения основного состояния в виде:

(14)
Подставляя (13), (14) в (12) найдем интегральное дисперсионное соотношение для возмущенной части поля в кинетической среде, которое при (для длинных волн)

(15)
Критическая длина волны находится из условия отсутствия роста возмущений и имеет вид:

(16)
Где

- продольная составляющая вектора скорости, поперечная составляющая.
Для максвелловского распределения (13)

, (17)
Что совпадает с гидродинамическим результатом (10). В области коротких волн езультаты гидродинамической и кинетической теорий различаются.
Похожие статьи
-
Релятивистская кинетическая теория - Гравитационные явления и гравитационная неустойчивость
Уравнения (12) нельзя применять, например, к такому агенту, как космические лучи. Если мы хотим использовать его для уточнения знаний о силах гравитации...
-
Примерно 70% галактик имеет спиральную структуру [10,11]. Спиральная структура галактик образуется образуется спиральными волнами плотности, возникающими...
-
Кластеры галактик - Гравитационные явления и гравитационная неустойчивость
Как видно из оценки (7), циклотронные радиусы релятивистских частиц имеют характерные размеры кластеров галактик (см. например [27] , [28]). Последние...
-
Гравитационное взаимодействие доминирует среди всех остальных взаимодействий на очень больших масштабах пространства-времени, сравнимых с...
-
Основные гипотезы механики сплошной среды Прежде всего, займемся изучением среды. Для ее описания необходимы полные и непротиворечивые модели движения...
-
Гравитационные волны - Черные дыры
Теория тяготения Эйнштейна предсказала существование гравитационных волн. Они подобны электромагнитным, которые являются быстро меняющимся...
-
Виды сплошной среды - Теория полета (аэродинамика и динамика полета)
Экспериментальные данные показывают, что большинство сред обладает специфическим свойством: отсутствием или малостью касательных напряжений pS, т. е....
-
Уравнения движения сплошной среды - Теория полета (аэродинамика и динамика полета)
В теоретической механике известно уравнение количества движения материальной точки: , Где в правой части равенства стоит сумма всех действующих на нее...
-
Термины механики сплошной среды - Теория полета (аэродинамика и динамика полета)
Скорость будем рассматривать как поле вектора в каждой точке пространства, задаваемой радиус-вектором этой точки с координатами x, y, z, в каждый момент...
-
Нецентральность гравитационного поля Земли - Возмущенное движение космического аппарата
Возмущенный движение гравитационный орбита При решении ограниченной задачи двух тел Земля представляется шаром со сферическим распределением плотности. В...
-
ГРАВИТАЦИОННАЯ БОМБА - Черные дыры
До сих пор, рассматривая процессы вокруг черной дыры и способы извлечения из нее энергии, мы убедились, что эту энергию можно извлечь либо в форме...
-
Виды полей (частиц) - Геометрия физического пространства
Уравнения 2.1.3.1...2.1.3.7 в зависимости от их сигнатуры делятся на два больших класса: 4.3.1 Фермионы - с одной временеподобной координатой : 2.1.3.6....
-
Образование черных дыр. Гравитационный коллапс, гравитационный радиус - Черные дыры
Ученые установили, что черные дыры должны возникать в результате очень сильного сжатия какой-либо массы, при котором поле тяготения возрастает настолько...
-
Что представляют из себя частицы Темной материи - Поиски Темной материи
Ясно, что эти частицы не должны распадаться на другие, более легкие частицы, иначе бы они распались за время существования Вселенной. Сам этот факт...
-
Образование черных дыр. Гравитационный коллапс. Гравитационный радиус - Черные дыры во вселенной
Ученые установили, что черные дыры должны возникать в результате очень сильного сжатия какой-либо массы, при котором поле тяготения возрастает настолько...
-
Динамика частиц - Геометрическая турбулентность и эволюция звезд
Кварки и преоны представляют собой частицы-фермионы, обладающие спином Ѕ и дробным электрическим зарядом - смотрите таблицы 1-2. Для описания динамики...
-
Образование звезд, стадия гравитационного сжатия - Эволюция и строение звезд
Согласно наиболее распространенной точке зрения, звезды образуются в результате гравитационной конденсации вещества межзвездной среды. Необходимое для...
-
Движение Частицы в Магнитном Поле - Магнитное поле Земли
В неоднородном магнитном поле движение частиц усложняется. Пусть мгновенная скорость частицы перпендикулярна плоскости чертежа. Тогда составляющая...
-
Исчезновение Солнца - Двигатель космолета на эффекте гравитационного самоускорения
Ограниченность скорости распространения гравитационного взаимодействия как следствие второго постулата СТО должно привести к весьма любопытному явлению -...
-
Цементация в разных средах, Газовая цементация - Химическая обработка, цементация
- Цементация в твердом карбюризаторе. - Цементация в твердом карбюризаторе с нагревом током высокой частоты (далее т. в. ч.). - Цементация в пастах. -...
-
Методика расчета направления неустойчивости - Космический аппарат
Эффективная коррекция орбиты КА в окрестности точки либрации подразумевает изменение скорости КА с целью компенсации влияния возрастающей компоненты (4)....
-
ИЗЛУЧЕНИЕ - Газопылевые комплексы. Межзвездная среда
Звездный ветер -- процесс истечения вещества из звезд в межзвездное пространство. Вещество, из которого состоят звезды, при определенных условиях может...
-
Объяснить аномалию зондов "Пионер" обнаруженный эффект гравитационного самоускорения, как оказалось, не позволяет. Однако, тот факт, что для ускорения...
-
ЭНЕРГИЯ ИЗ ГРАВИТАЦИОННОЙ БЕЗДНЫ. БЕЗДОННЫЕ ЧЕРНЫЕ ДЫРЫ - Черные дыры
Мы уже неоднократно говорили, что излучение гравитационных волн телом, кружащимся около черной дыры, является способом получения энергии. Но это не есть...
-
ГРАВИТАЦИОННЫЙ ВИХРЬ ВОКРУГ ЧЕРНОЙ ДЫРЫ - Черные дыры
По теории Ньютона, гравитационное поле никак не зависит от движения вещества. Так, поля тяготения неподвижного шара и вращающегося совершенно одинаковы,...
-
Безопорное движение&;nbsp; - Двигатель космолета на эффекте гравитационного самоускорения
Такое "вытягивание" потенциала, зависящего от скорости удаления Солнца, наводит на интересную мысль. А что, если "получатель потенциала", скажем,...
-
Силы и моменты в механике сплошной среды Силы, распределенные по объему W, называются объемными или массовыми. Они обозначаются и относятся к элементу...
-
Эффективная коррекция орбиты КА в окрестности точки либрации подразумевает изменение скорости КА с целью компенсации влияния возрастающей компоненты (4)....
-
Интерполяция направления неустойчивости - Космический аппарат
Зависимость направления неустойчивости от координат X, Y КА образует поверхность, проекции которой представлены на рис. 36-38. Рис. 36. Точки, для...
-
Вариации скорости движения Солнца вокруг центра масс солнечной системы можно рассчитать на основании уравнения движения Где X, y, z - координаты точки С...
-
НЛО, НЛО и другие аномальные явления - Проблема внеземных цивилизаций
НЛО и другие аномальные явления Уфологи до сих пор спорят о происхождении НЛО и других аномальных явлений, в частности, так хорошо всем известного...
-
Бомбардировка энергичными частицами - Солнце
Помимо непрерывно "дующего" солнечного ветра наше светило служит источником энергичных заряженных частиц (в основном протонов, ядер атомов гелия и...
-
Инфузионные среды, Коллоидные инфузионные растворы - Медицинские препараты на основе декстрана
Инфузионные среды - препараты, применяемые для парентеральной жидкостной терапии. Все инфузионные среды, или растворы, в зависимости от свойств и...
-
Вспышки на Солнце и их воздействие на Землю - Физика солнечных явлений
В процессе развития активной области иногда возникают ситуации, при которых возможна быстрая перестройка ("перезамыкание") магнитных полей. Эта...
-
ЗА КРАЕМ ГРАВИТАЦИОННОЙ БЕЗДНЫ - Черные дыры
До сих пор мы говорили о процессах вокруг черной дыры. Обратимся теперь к самому захватывающему и интригующему: попробуем подойти к границе черной дыры...
-
Теория элементарных частиц и принцип целесообразности - Астрономия и современная картина мира
1. Наша Вселенная - лучший из миров Панглос: Все события неразрывно связаны в лучшем из возможных миров. Кандид: Если это лучший из возможных миров, то...
-
Влияние Луны на Землю - Исследование явления удаления Луны от Земли
Луна спутник земля На протяжении многих столетий человечество интересовалось Луной. Первые оптические инструменты, типа галлилеевской трубы, направленные...
-
ГРАВИТАЦИОННЫЙ РАДИУС - Черные дыры
Чем же отличается теория тяготения Эйнштейна от теории Ньютона? Начнем с простейшего случая. Предположим, что мы находимся на поверхности сферической...
-
Черная дыра в представлении художника, Примеры гравитационных воронок - Строение Солнца
Черные дыры настолько массивны, что их вторая космическая скорость быстрее, чем скорость света. Поскольку ничего не может двигаться быстрее, чем свет, то...
-
ТУМАННОСТИ - Газопылевые комплексы. Межзвездная среда
Туманность -- участок межзвездной среды, выделяющийся своим излучением или поглощением излучения на общем фоне неба. Туманности состоят из пыли, газа и...
Гравитационная неустойчивость сред и пучков частиц - Гравитационные явления и гравитационная неустойчивость