Безопорное движение&;nbsp; - Двигатель космолета на эффекте гравитационного самоускорения

Такое "вытягивание" потенциала, зависящего от скорости удаления Солнца, наводит на интересную мысль. А что, если "получатель потенциала", скажем, измерительный прибор не покоится, а тоже движется со скоростью Солнца? При неподвижных Солнце и приборе все ясно: потенциал всегда один и тот же. Но при движении Солнца потенциал не просто движется за ним, а немного отстает, что приводит к его своеобразному "вытягиванию", "растяжению", запаздыванию. Если измерительный прибор находится на фиксированном расстоянии от Солнца, двигаясь с точно такой же скоростью, что и оно, то он, тем не менее, должен зафиксировать изменение потенциала. Причем очевидно, что прибор будет фиксировать увеличение этого потенциала.

Поскольку скорость объектов одна и та же, им можно назначить одну и ту же систему отсчета и даже связать их неким условным стержнем. Поскольку стержнем соединиться с Солнцем нельзя, рассмотрим другой объект. Пусть два точечных тела равной массы m соединены твердым невесомым стержнем длиной r. Если эта система изначально находится в прямолинейном равномерном движении вдоль своей оси, то, как мы обнаружили в примере с Солнцем, на заднюю массу будет действовать дополнительная сила притяжения от головной точки по сравнению с состоянием покоя. А это непосредственно означает, что эта сила не будет уравновешена силой упругого сжатия стержня и приведет эту массу в ускоренное движение.

Но, можно возразить, такая же сила, вероятно, действует и на головную массу, тормозя систему? Нет! Для головной массы действует эффект в точности противоположный. Гравитационный потенциал ведомой массы отстает от ведущей, поэтому ведущая масса оказывается под воздействием уменьшенной силы от притяжения ведомой. Поэтому она так же не будет уравновешена силой сжатия стержня, и стержень будет толкать эту массу вперед.

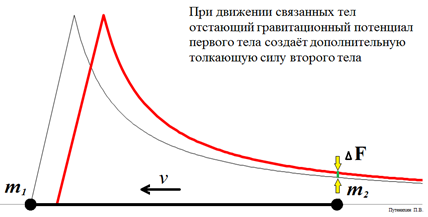
массы на концах движущегося стрежня испытывают неуравновешенную силу, превышающую силу их гравитационного притяжения в состоянии покоя

Рис. 4. Массы на концах движущегося стрежня испытывают неуравновешенную силу, превышающую силу их гравитационного притяжения в состоянии покоя

Выходит, что стержень под воздействием этих неожиданных сил начнет ускоряться. Причем, из состояния покоя стержень сам в движение не придет, ему необходимо дать некоторую начальную скорость вдоль его оси.

Конечно, можно возразить: дополнительная сила притяжения просто сожмет стержень, и он станет короче. Но этого не может произойти. Деформация отстающего конца стержня постепенно (не быстрее скорости света) передастся на его передний край, конец стержня будет стремиться переместиться вперед. Этому будет препятствовать ведущая масса. За счет чего? Сила притяжения этой массы от отстающего тела всегда меньше той, что соответствует исходной, "несжатой" длине стержня, поскольку для ведущей массы расстояние до ведомой "кажется" более длинным. Поэтому в ведущей, передней по движению массы не появится дополнительной силы, чтобы компенсировать возросшую силу давления от связующего стержня.

Давайте оценим величину этих сил и возникшего от их действия ускорения. В состоянии покоя массы притягиваются с силой согласно закону Ньютона:

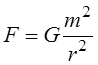
Где

F - сила притяжения точечных масс;

M - массы на концах стержня;

R - длина стержня;

G - гравитационная постоянная.

Путь стержень движется со скоростью v вдоль своей оси. За некоторый момент времени ведущая масса переместится из точки a в точку a', а ведомая - из точки b в точку b'. Из точки a' гравитационный потенциал ведущей массы начал создавать обновленные значения поля в направлении ведомой массы со скоростью света - с. До того момента, когда фронт прибудет в точку b', там "действует" прежнее, большее значение потенциала.

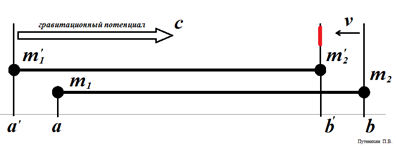
масса в конце движущегося стрежня испытывают силу, как если бы длина стержня была меньше исходной

Рис.5. Масса в конце движущегося стрежня испытывают силу, как если бы длина стержня была меньше исходной

Ведомая масса движется навстречу этому фронту со скоростью v, находясь в поле с последним значением потенциала. Поскольку на начало движения расстояние между массами было равно r, фронт от ведущей массы встретится с ведомой массой в точке, отмеченной красной чертой, через времяt = r / (c + v). За это время ведомая масса приблизится к точке, из которой началось движение фронта нового значения потенциала, на расстояние b - b' = r1 = vt = rv / (c + v). Следовательно, ведомая масса окажется в точке с потенциалом, соответствующим этому измененному расстоянию

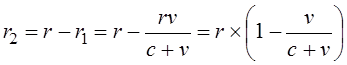
В дальнейших расчетах будем скорость движения стержня измерять в долях от скорости света v = kc, назвав для наглядности эту безразмерную величину kтой же буквой v, что и размерную скорость стержня:

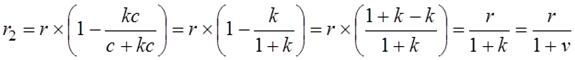
Итак, мы видим, что при движении стержня массы m на его концах притягиваются с силой, которая соответствует уменьшенной длине стержня. Эта сила притяжения равна:

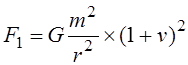
Дополнительная сила, не уравновешенная сжатым связующим стержнем, таким образом, равна:

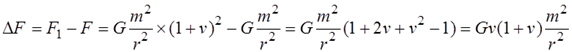
Сила эта, следовательно, приводит к ускоренному движению ведомой массы с ускорением:

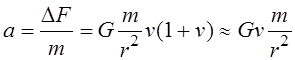
Казалось бы, нам при вычислении ускорения следовало взять удвоенную массу, поскольку это и есть масса всего стержня. Но очевидно, что точно такая же сила действует и на ведущую массу, приводя ее в точно такое же ускоренное движение, что, в конечном итоге, приведет к полученному выражению.

Итак, мы обнаружили довольно странный эффект: к стержню не прикладывается никаких внешних сил, а он движется ускоренно! Причем эффект, имеющий строгое математическое обоснование. Такое движение явно выглядит как безопорное или, как его иногда называют, эфироопорное.

Парадокс? Нет!

Однако, строгие правила теории относительности требуют в обязательном порядке проверить выкладки и с точки зрения другой системы отсчета. И здесь нас, как может показаться, встречает неприятная неожиданность. Действительно, с точки зрения системы отсчета стержня, которая вроде бы должна считаться инерциальной, расстояние между массами неизменно, ничто не мешает гравитационному потенциалу, однажды распространившись, остаться неизменным навсегда. То есть, с точки зрения ИСО стержня исчезает причина для ускоренного движения. Налицо явные признаки парадокса: теория относительности для двух разных систем отсчета дает два взаимоисключающих предсказания. В лабораторной, неподвижной системе отсчета мы вычислили ускорение, с которым, якобы, должен двигаться стержень с массами на конце, а в системе отсчета стержня мы не обнаружили никаких сил, способных привести стержень в ускоренное движение.

Однако, это кажущийся парадокс. Таких взаимоисключающих предсказаний специальная теория относительности не делает. Хотя бы потому, что она делает только одно предсказание: с точки зрения неподвижной, Земной системы отсчета. В этой ИСО мы и получили эффект ускоренного движения без приложения внешней силы.

А как же в системе отсчета стержня? Почему мы лишаем специальную теорию относительности права сделать не подходящее для нас предсказание? Дело в том, что на самом деле система отсчета стержня не является инерциальной. Неспроста я ее всегда называл системой отсчета, без указания "инерциальная". Действительно, наблюдатель, находящийся на стержне легко обнаружит, что там действуют эквивалентные силы гравитации. Помимо сил гравитации, создаваемых массами на концах стержня. Все свободно висящие предметы будут постепенно перемещаться к ведомой массе. Если их принудительно переместить к ведущей, то они все равно переместятся обратно - к ведомой. Если взять пружинный динамометр, то он обязательно вытянется вдоль стержня и будет показывать некоторую силу. Здесь мы оставляем без внимания тот факт, что дополнительная сила существенно меньше сил притяжения масс.

Ну, так и что с того? Мы здесь имеем некоторое подобие парадокса близнецов. Да, с точки зрения специальной теории относительности в системе отсчета стержня нет никаких сил, приводящих его в ускоренное движение. Но есть загадочная сила, не имеющая видимого источника. Для СТО нет никакой разницы - есть источник, нет источника - она обязана к своему предсказанию добавить эту гравитационную поправку. СТО не имеет права утверждать и не утверждает, что ускоренного движения нет. Ускоренное движение не анализируется здесь по правилам, законам специальной теории относительности, но это не означает, что другие законы не действуют.

Тем не менее, это, как говорится, не ее, СТО, проблемы. Она сделала свои непротиворечивые предсказания, а почему одно из них не выполняется - не ее проблема, ищите виновника. И кто же этот загадочный источник ускорения? Как ни странно, он все-таки в недрах специальной теории относительности! Это второй постулат (принцип) теории. Прямым следствием из этого принципа является предельность скорости любого сигнала, в том числе и скорости распространения фронта гравитационного поля.

Никакого безопорного или эфироопорного движения в данном случае нет. Есть удивительный эффект возникновения разницы сил из-за того, что тянущая сила не успевает уменьшиться при удалении притягивающего тела. Притягивающее тело удалилось, и сила притяжения, казалось бы, должна уменьшиться. Но эффект снижения силы притяжения приходит к ведомому телу с опозданием и оно не знает, что источник силы удалился, поэтому "чувствует" увеличившуюся силу притяжения, как если бы оно и на самом деле приблизилось к неподвижному притягивающему телу.

Похожие статьи




Безопорное движение&;nbsp; - Двигатель космолета на эффекте гравитационного самоускорения

Предыдущая | Следующая