Термины механики сплошной среды - Теория полета (аэродинамика и динамика полета)
Скорость будем рассматривать как поле вектора в каждой точке пространства, задаваемой радиус-вектором этой точки с координатами x, y, z, в каждый момент времени t:
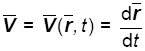
(1.1)
Или по координатам:
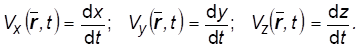
(1.2)
Очевидный смысл этих уравнений заключается в том, что скорость определяется, как производная по времени от функции местоположения частицы cреды (x, y,z, t).
Уравнения (1.1) или (1.2), задающие положение (x, y,z, t) частицы в пространстве в каждый момент времени как решение дифференциального уравнения, можно рассматривать как траекторию ее движения.
Если поле вектора скорости сплошной среды
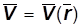
Не зависит от времени в каждой точке пространства, то движение называется стационарным или установившимся. В общем случае
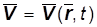
И движение называется нестационарным или неустановившимся.
Линиями тока в механике сплошной среды называются линии, которые в каждый фиксированный момент времени имеют в каждой своей точке касательные, совпадающие с вектором скорости. Таким образом, частицы среды, попавшие на линию тока, не имеют составляющей скорости поперек нее и не могут ее пересечь. Линии тока необходимы для получения в теории математически строгих выводов. На практике линии тока в прозрачной жидкости с взвешенными частицами нерастворимой краски можно зафиксировать фотографированием с маленькой выдержкой короткие следы этих частиц, сливаясь, вырисовывают линии тока. Уравнение линии тока в момент времени t запишется в терминах аналитической геометрии, как условие коллинеарности векторов:
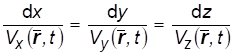
.(1.3)
Таким образом, картина линий тока в нестационарном движении все время меняется. При установившемся движении отсутствие в уравнении (1.3) времени t приводит к совпадению линий тока с траекториями частиц.
Трубчатая поверхность, образованная линиями тока, проходящими через некоторую замкнутую кривую, называется трубкой тока. Частицы сплошной среды не пересекают стенок трубки тока, не имея нормальных к ним составляющих скорости.
Если компоненты вектора скорости не обращаются в нуль и вместе со своими первыми производными однозначны и не имеют разрывов, то решение уравнения (1.3) существует и единственно. В противоположном случае существование или единственность может нарушаться, т. е. в некоторых точках пространства линии тока могут ветвиться или вырождаться в точку. Такие точки называются особыми или критическими.
Напомним некоторые математические термины [4] применительно к скорости, заданной в пространстве полю скоростей.
Вектором будем обозначать поверхность с указанным направлением нормали, выражающимся через единичные векторы осей координат:

,
А скаляром S только площадь этой поверхности.
Потоком скорости через поверхность с заданным вектором нормали называется поверхностный интеграл
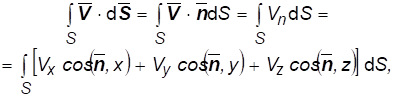
(1.4)
Где Vn обозначает проекцию скорости на единичный вектор нормали к поверхности.
Градиентом называется векторная функция скаляра:
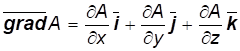
.(1.5)
Ротор скорости (вихрь) определяется формулой:
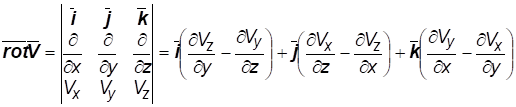
,(1.6)
А дивергенция скорости:
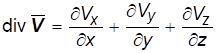
.(1.7)
Циркуляцией скорости по замкнутому контуру L с определенным направлением обхода называется криволинейный интеграл:
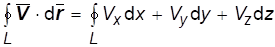
.(1.8)
Известные теоремы векторных полей [4] применимы и к полю скоростей. Теорема Стокса:
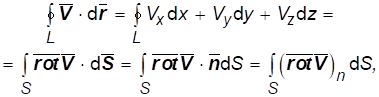
(1.9)
Справедлива при ориентации обхода контура L и нормали к натянутой на него поверхности по правилу правого винта, а теорема Остроградского-Гаусса:
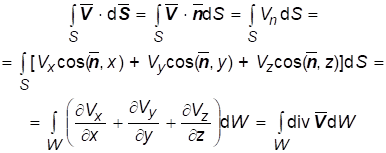
(1.10)
При условии, что замкнутая поверхность ограничивает объем W.
Полную производную по времени от скаляра A(,t) можно определить по известной [4] формуле:
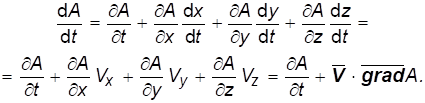
(1.11)
Производную
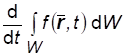
От интеграла по произвольному подвижному объему W, где от t зависит не только подынтегральная функция, но и объем, вычислим с помощью определения производной:
В последнем пределе W'W образуется сдвигом элементарных площадок dS поверхности S, ограничивающей W, на расстояние VndS. Кроме того, при
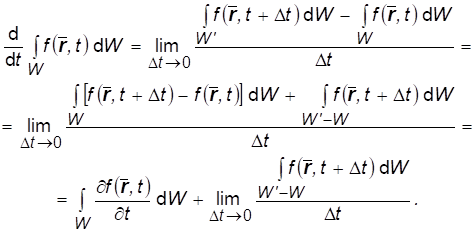
T 0: f(,t+t) f(,t)
И деформированная поверхность S S, поэтому предел принимает значение
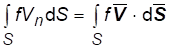
(сравните с (1.4)) или
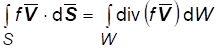
По теореме Остроградского-Гаусса (1.10). Откуда в силу уравнения (1.11):
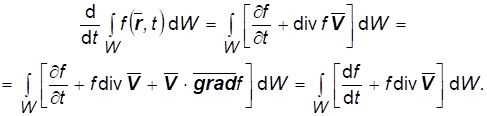
(1.12)
Вектор
0
Тоже можно рассматривать, как поле вектора ротора скорости
(,t)
вихревое поле. Непосредственной проверкой легко убедиться, что всегда
Div = 0.
Отсюда по теореме Остроградского-Гаусса следует, что поток ротора скорости сквозь любую замкнутую поверхность равен нулю:
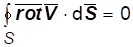
.(1.13)
В вихревом поле по аналогии с полем скоростей выделяют вихревую линию:
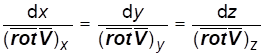
(1.14)
И вихревую трубку. Так как через боковую поверхность вихревой трубки по определению нет потока ротора скорости, то из (1.13) вытекает постоянство такого потока через любое ее поперечное сечение (первая кинематическая теорема Гельмгольца о вихрях). Эта величина называется интенсивностью вихревой трубки. Согласно теореме Стокса (1.9) она равна циркуляции скорости по контуру, образующему вихревую трубку:
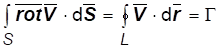
.(1.15)
Похожие статьи
-
Безвихревое и вихревое движение - Теория полета (аэродинамика и динамика полета)
Движение сплошной среды в некоторой области называется безвихревым, если в ней = 0, И вихревым, если 0 Хотя бы в части этой области, называемой вихрем....
-
Уравнение неразрывности - Теория полета (аэродинамика и динамика полета)
Как известно, плотность вещества в физике вводится предельным переходом: , Где в механике сплошной среды следует понимать под m массу вещества,...
-
Силы и моменты в механике сплошной среды Силы, распределенные по объему W, называются объемными или массовыми. Они обозначаются и относятся к элементу...
-
Основные гипотезы механики сплошной среды Прежде всего, займемся изучением среды. Для ее описания необходимы полные и непротиворечивые модели движения...
-
Виды сплошной среды - Теория полета (аэродинамика и динамика полета)
Экспериментальные данные показывают, что большинство сред обладает специфическим свойством: отсутствием или малостью касательных напряжений pS, т. е....
-
Уравнения движения сплошной среды - Теория полета (аэродинамика и динамика полета)
В теоретической механике известно уравнение количества движения материальной точки: , Где в правой части равенства стоит сумма всех действующих на нее...
-
ВВЕДЕНИЕ - Теория полета (аэродинамика и динамика полета)
Теория полета (аэродинамика и динамика полета) наука фундаментальная и строгая, опирающаяся на математический аппарат. Но, как и о всякой науке, о ней...
-
Путь, описываемый космическим аппаратом в пространстве наз. траекторией. Прямолинейные траектории. Если начальная скорость равна нулю, то тело начинает...
-
Небесная механика и некоторые ее задачи - Классические теории гравитации
Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации, называется небесной механикой. Наиболее простой задачей...
-
Введение - Теория свободного полета в полях тяготения
Главным звеном в цепи космических дисциплин является теория движения космических объектов. В этом докладе рассматривается одна из ее составных частей -...
-
Релятивистская кинетическая теория - Гравитационные явления и гравитационная неустойчивость
Уравнения (12) нельзя применять, например, к такому агенту, как космические лучи. Если мы хотим использовать его для уточнения знаний о силах гравитации...
-
Теория единого поля - альтернативное мнение
Данная статья есть выдержка из книги первой: "Теория единого поля - альтернативное мнение". Книга представляет собой альтернативный, господствующей...
-
Тел и метод численного интегрирования - Теория свободного полета в полях тяготения
Пассивное движение космического аппарата в мировом пр-ве происходит в основном под действием сил притяжений небесных тел - Земли, Луны, Солнца, планет....
-
Теория Большого взрыва была придумана для того, чтобы объяснить происхождение вселенной. Почему-то из знакомства с ней обычно выносят больше вопросов,...
-
В гравитирующих средах под влиянием гравитации могут образовываться структуры. Задачу звездообразования в нерелятивистском газе впервые рассмотрел...
-
Аномальные радиальные колебания орбит - Аномальное движение орбит в общей теории относительности
В общем случае уравнения движения материальной точки в гравитационном поле имеют вид [3,6,11-12] (39) Вычисляя коэффициенты аффинной связности в метрике...
-
Центральное поле тяготения - Теория свободного полета в полях тяготения
Когда космический аппарат находиться в мировом пространстве вдали от планет, достаточно учитывать притяжение одного лишь Солнца, потому что...
-
Исчезновение Солнца - Двигатель космолета на эффекте гравитационного самоускорения
Ограниченность скорости распространения гравитационного взаимодействия как следствие второго постулата СТО должно привести к весьма любопытному явлению -...
-
Развитие космической техники - Полеты человека в космос
Издревле человека волновала и манила бездонная высь неба, усыпанная мириадами звезд. Они (звезды) указывали путь мореходам и путешественникам, давали...
-
Уравнения гравитационного поля Эйнштейна имеют вид [4-8]: (1) - тензор Риччи, метрический тензор и тензор энергии-импульса; - космологическая постоянная...
-
Отсутствуют ощутимые в обычных (земных) условиях гравитационные силы, которые действуют перпендикулярно (нормально) к средней плоскости движения планет....
-
В данной статье не оспариваются существующие научные догмы и теории, автор пробует объяснить данные природные явления с другой точки зрения. Подобные...
-
НЕБЕСНАЯ МЕХАНИКА ЧЕРНЫХ ДЫР - Черные дыры
Согласно теории тяготения Ньютона любое тело в гравитационном поле звезды движется либо по разомкнутым кривым - гиперболе или параболе, - либо по...
-
Представление основных уравнений динамики в динамичном пространстве-материи - О суперквазаре
Для кванта динамичного пространства-материи, динамика квантового поля взаимодействия, характеризуется в Евклидовом пространстве-времени проекцией радиуса...
-
Специальная Теория Относительности (СТО) - О суперквазаре
Нельзя определить или траекторию квантов НОЛ, пространства-материи, по одной прямой в динамичном пучке параллельных прямых линий. Этот физический принцип...
-
Расширяющаяся вселенная - Теории происхождения Вселенной
Заглянуть глубже в тайны мироздания, чем это сделал Ньютон, долгое время казалось невозможным. Лишь в начале нашего века в 1915 году появилась работа А....
-
ФИЗИЧЕСКИЕ ОСОБЕННОСТИ МЗС - Газопылевые комплексы. Межзвездная среда
- Отсутствие локального термодинамического равновесия (ЛТР) - состояния системы, при котором остаются неизменными по времени макроскопические величины...
-
ИЗЛУЧЕНИЕ - Газопылевые комплексы. Межзвездная среда
Звездный ветер -- процесс истечения вещества из звезд в межзвездное пространство. Вещество, из которого состоят звезды, при определенных условиях может...
-
Причины и принцип движения Луны относительно Земли не значительно отличаются от движения Земли относительно Солнца, смотри Раздел 3. Принципиальная схема...
-
Невесомость - Факторы космического полета
Теоретически в межзвездном пространстве нет точки, где бы не сказывалась сила притяжения. Поэтому даже в условиях космического полета на тела будут...
-
Ускорение - Факторы космического полета
В течение очень длительного времени считалось, что большие скорости передвижения оказывают вредное влияние на человека, а скорость в 500 км/ч является...
-
Метеорные тела - Факторы космического полета
В безоблачные ночи нередко можно наблюдать "падающие звезды" - метеоры, которые быстро проносятся по темному небосводу. Это происходит вследствие их...
-
Какие воздействия и как они влияют на Землю, во время прохождения Земли по определенным участкам орбиты за один период обращения вокруг Солнца, согласно...
-
Нейтронные звезды - Особенности теории конца жизни звезд
Существование нейтронных звезд - звезд, состоящих из вырожденных нейтронов - предсказывалось теоретиками еще в 30-х годах (первым это понял...
-
Космические лучи, Межзвездное магнитное поле - Газопылевые комплексы. Межзвездная среда
Космимческие лучим -- элементарные частицы и ядра атомов, движущиеся с высокими энергиями в космическом пространстве. Их основным (но не единственным)...
-
"Движение" в пространстве событий, "Движение" тела отсчета - Геометрия физического пространства
"Движение" тела отсчета "Движение" тела отсчета -- перемещение начала (нулевой точки) системы координат, связанной с телом отсчета, по мировой линии...
-
Лирика - Геометрия физического пространства
Итак, попытаемся разобраться, что же у нас получилось. Наличие ненаблюдаемых координат приводит к существенному ограничению восприятия окружающего нас...
-
Орбиту можно получить как линию пересечения двух поверхностей. Уравнение одной поверхности - это уравнение плоскости орбиты. Уравнение второй поверхности...
-
Невесомость При невесомости притяжение Земли (или другого небесного тела ) не будут вмешиваться в перемещения предметов относительно корабля. Отсутствуют...
-
Как создать машину времени? - Черные дыры во вселенной
Теории о путешествиях во времени, пожалуй, остаются одними из самых впечатляющих вслед за разработками в области телепортации, торсионных полей и...
Термины механики сплошной среды - Теория полета (аэродинамика и динамика полета)