Моделирование простейшего потока заявок


Цель работы: изучение свойств и характеристик пуассоновского (простейшего) потока. Сравнение теоретических и модельных значений полученных характеристик.

Порядок выполнение работы.

1. Генерируем псевдослучайные равномерно распределенные числа на интервале [0,1], используя пакет MATLAB. Для этого используется функция rand. Функция rand(n, m) возвращает прямоугольную матрицу размерности n m со случайными числами.

Для получения выборки из n = 100 равномерно распределенных псевдослучайных чисел:

>> rand(1,100)

Ans =

Columns 1 through 8

0.9501 0.2311 0.6068 0.4860 0.8913 0.7621 0.4565 0.0185

Columns 9 through 16

0.8214 0.4447 0.6154 0.7919 0.9218 0.7382 0.1763 0.4057

Columns 17 through 24

0.9355 0.9169 0.4103 0.8936 0.0579 0.3529 0.8132 0.0099

Columns 25 through 32

0.1389 0.2028 0.1987 0.6038 0.2722 0.1988 0.0153 0.7468

Columns 33 through 40

0.4451 0.9318 0.4660 0.4186 0.8462 0.5252 0.2026 0.6721

Columns 41 through 48

0.8381 0.0196 0.6813 0.3795 0.8318 0.5028 0.7095 0.4289

Columns 49 through 56

0.3046 0.1897 0.1934 0.6822 0.3028 0.5417 0.1509 0.6979

Columns 57 through 64

0.3784 0.8600 0.8537 0.5936 0.4966 0.8998 0.8216 0.6449

Columns 65 through 72

0.8180 0.6602 0.3420 0.2897 0.3412 0.5341 0.7271 0.3093

Columns 73 through 80

0.8385 0.5681 0.3704 0.7027 0.5466 0.4449 0.6946 0.6213

Columns 81 through 88

0.7948 0.9568 0.5226 0.8801 0.1730 0.9797 0.2714 0.2523

Columns 89 through 96

0.8757 0.7373 0.1365 0.0118 0.8939 0.1991 0.2987 0.6614

Columns 97 through 100

0.2844 0.4692 0.0648 0.9883

После исполнения команды получили квадратную матрицу десятого порядка, элементами которой являются случайные числа на интервале [0; 1].

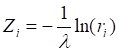
2. Найдем длины промежутков времени между последовательными вызовами: , где i =1, 2, ... . Zi - длины промежутков времени между последовательными вызовами.

Интенсивность потока заявок л определяется из условия: = 10(N+1)/(N+4) (выз/мин); где N - номер по журналу: л=7.273

>> z=-1/7.273*log(ans)

Z =

Columns 1 through 14

0.0070 0.2014 0.0687 0.0992 0.0158 0.0374 0.1078 0.5486 0.0271 0.1114 0.0667 0.0321 0.0112 0.0417

Columns 15 through 28

0.2387 0.1240 0.0092 0.0119 0.1225 0.0155 0.3917 0.1432 0.0284 0.6351 0.2714 0.2194 0.2222 0.0694

Columns 29 through 42

0.1789 0.2221 0.5749 0.0401 0.1113 0.0097 0.1050 0.1197 0.0230 0.0886 0.2195 0.0546 0.0243 0.5404

Columns 43 through 56

0.0528 0.1332 0.0253 0.0945 0.0472 0.1164 0.1634 0.2286 0.2259 0.0526 0.1643 0.0843 0.2600 0.0495

Columns 57 through 70

0.1336 0.0207 0.0218 0.0717 0.0963 0.0145 0.0270 0.0603 0.0276 0.0571 0.1475 0.1703 0.1478 0.0862

Columns 71 through 84

0.0438 0.1613 0.0242 0.0778 0.1366 0.0485 0.0831 0.1114 0.0501 0.0654 0.0316 0.0061 0.0892 0.0176

Columns 85 through 98

0.2413 0.0028 0.1793 0.1893 0.0182 0.0419 0.2738 0.6109 0.0154 0.2219 0.1661 0.0568 0.1729 0.1040

Columns 99 through 100

    0.3763 0.0016 3. На промежутке [T1 ; T2 ]: T1 = N+1, T2 =N+4 мин.

Получим последовательность tK моментов поступления вызовов: Т1 = 8, Т2 = 11

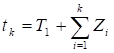
до тех пор пока tK T2

Для этой операции необходимо написать программу на языке программирования системы MATLAB.

>> w=0;

For k = 1:100;

W=w+z(1,k);

For n = 1:k;

End

T(1,n)= 2+w;

End

T

T =

T =

Columns 1 through 14

2.0070 2.2084 2.2771 2.3763 2.3921 2.4295 2.5373 3.0859 3.1129 3.2244 3.2911 3.3232 3.3344 3.3761

Columns 15 through 28

3.6148 3.7388 3.7480 3.7599 3.8824 3.8979 4.2896 4.4328 4.4613 5.0964 5.3678 5.5872 5.8094 5.8788

Columns 29 through 42

6.0577 6.2798 6.8547 6.8949 7.0062 7.0159 7.1209 7.2406 7.2635 7.3521 7.5716 7.6262 7.6505 8.1909

Columns 43 through 56

8.2436 8.3769 8.4022 8.4967 8.5439 8.6603 8.8237 9.0523 9.2782 9.3308 9.4951 9.5794 9.8394 9.8889

Columns 57 through 70

10.0225 10.0432 10.0650 10.1367 10.2330 10.2475 10.2745 10.3348 10.3624 10.4195 10.5671 10.7374 10.8852 10.9715

Columns 71 through 84

11.0153 11.1766 11.2009 11.2786 11.4152 11.4637 11.5467 11.6581 11.7082 11.7736 11.8052 11.8113 11.9005 11.9181

Columns 85 through 98

12.1593 12.1621 12.3414 12.5308 12.5490 12.5909 12.8647 13.4756 13.4911 13.7129 13.8791 13.9359 14.1088 14.2128

Columns 99 through 100

    14.5891 14.5907 4. Полученные данные свести в таблицу 1, где ri - столбец из массива случайных чисел (ans); Zi - столбец из массива длин промежутков времени между последовательными вызовами; ti - столбец из массива моментов поступления вызовов, полученный после выполнения программы:

Таблица 1.

Ri

Zi

Tk

0,950129285147175 0,231138513574288 0,606842583541787 0,4859824687093 0,891298966148902 0,762096833027395 0,456467665168341 0,018503643248224 0,821407164295253 0,444703364353194 0,615432348100095 0,791937037427035 0,921812970744802 0,738207245810665 0,176266144494618 0,405706213062096 0,935469699107606 0,916904439913408 0,410270206990945 0,893649530913534 0,057891304784269 0,352868132217 0,813166497303758 0,009861300660924 0,13889088195695 0,202765218560273 0,19872174266149 0,603792479193819 0,27218792496996 0,198814267761062 0,015273927029036 0,746785676564429 0,445096432287947 0,931814578461665 0,465994341675424 0,418649467727506

0,007033853158023 0,201393939543707 0,068676729924699 0,099213904626273 0,015822269734951 0,037354826605991 0,107828600784772 0,548575228097076 0,027050234489701 0,111418646507569 0,066744156899094 0,032073888151526 0,011193857787638 0,041733902505542 0,238658083530224 0,124037672825837 0,009171803085828 0,011927955675608 0,122499559317324 0,015460140830003 0,391748670716115 0,14322299669539 0,028436600669619 0,63510754931868 0,271423989555195 0,219401420058712 0,22217100382836 0,06936954730885 0,178916891327272 0,222107000950519 0,574949542140788 0,040145338546155 0,111297170152848 0,009710083079634 0,104988558676973 0,119719689500153

2,007033853158023 2,20842779270173 2,277104522626428 2,376318427252702 2,392140696987652 2,429495523593644 2,537324124378416 3,085899352475492 3,112949586965193 3,224368233472762 3,291112390371856 3,323186278523381 3,33438013631102 3,376114038816562 3,614772122346786 3,738809795172623 3,74798159825845 3,759909553934058 3,882409113251382 3,897869254081384 4,289617924797499 4,432840921492889 4,461277522162508 5,096385071481188 5,367809061036382 5,587210481095095 5,809381484923455 5,878751032232305 6,057667923559578 6,279774924510097 6,854724466650885 6,89486980519704 7,006166975349889 7,015877058429523 7,120865617106496 7,24058530660665

Продолжение таблицы 1.

Ri

Zi

Tk

0,846221417824324 0,525152496305172 0,202647357650387 0,672137468474288 0,838118445052387 0,019639513864818 0,681277161282135 0,379481018027998 0,831796017609606 0,502812883996251 0,709471392703387 0,428892365340997 0,304617366869394 0,189653747547175 0,193431156405215 0,682223223591384 0,302764400776609 0,541673853898088 0,150872976149765 0,697898481859863 0,378373000512671 0,86001160488682 0,853655130662768 0,593562912539682 0,496552449703103 0,89976917516961 0,821629160735343 0,644910384193844 0,817974340839245 0,660227556441602 0,341970618270216 0,289725895856238 0,341193569414884 0,5340790176266 0,727113216929677 0,309290159790958 0,83849604493808 0,568072461007776 0,370413556632116

0,022958095754552 0,088555835200853 0,219481364632804 0,054625655602615 0,024281018279026 0,540383848296809 0,052768604981097 0,133225725528525 0,025322155831512 0,094532817007977 0,047193056999396 0,116396162267975 0,163439959413831 0,228592774743483 0,225881150923818 0,052577803846183 0,164278885070577 0,084296879449953 0,260046337651654 0,04945436934675 0,133627773416852 0,02073551433675 0,021755533482455 0,071718969882587 0,096255487721428 0,014521795763257 0,027013079661647 0,060311276099775 0,027626056790673 0,057083833479749 0,147536155245529 0,170331361154251 0,147848935859913 0,086238344271326 0,043815905664217 0,161346818953127 0,024219086286258 0,077754199945117 0,136550966162678

7,263543402361202 7,352099237562054 7,571580602194858 7,626206257797474 7,6504872760765 8,19087112437331 8,243639729354406 8,376865454882932 8,402187610714442 8,496720427722419 8,543913484721816 8,660309646989791 8,823749606403624 9,052342381147106 9,278223532070923 9,330801335917105 9,495080220987683 9,579377100437636 9,839423438089291 9,88887780743604 10,022505580852894 10,043241095189645 10,0649966286721 10,136715598554687 10,232971086276116 10,247492882039372 10,274505961701019 10,334817237800793 10,362443294591467 10,419527128071216 10,567063283316745 10,737394644470996 10,88524358033091 10,971481924602235 11,015297830266453 11,17664464921958 11,20086373550584 11,278617935450956 11,415168901613635

Продолжение таблицы 1.

Ri

Zi

Tk

0,702739913240377 0,546571151829106 0,444880204672912 0,694567240425548 0,621310130795413 0,794821080200926 0,956843448444877 0,522590349080708 0,880142207411327 0,172956141275237 0,979746896788841 0,2714472586418 0,25232934687399 0,875741899818074 0,737305988465256 0,13651874225971 0,011756687353118 0,893897966445253 0,199138067205738 0,298723012102214 0,661442576382325 0,284408589749945 0,469224285211001 0,064781122963272 0,988334938277631

0,048503839209029 0,083059368123408 0,111363981306166 0,050112237454562 0,065437222087503 0,031574074798271 0,006065651952815 0,08922829550264 0,0175542121868 0,241264572427594 0,002813283274771 0,179291546490461 0,189333165505756 0,018243347500345 0,041901868811221 0,273792570858075 0,61093538620282 0,015421922427488 0,221883251722143 0,166126566186786 0,0568310336017 0,172878231603228 0,104038829201228 0,376287780882546 0,001613313946111

11,463672740822664 11,546732108946072 11,658096090252238 11,708208327706801 11,773645549794304 11,805219624592574 11,811285276545389 11,900513572048029 11,918067784234829 12,159332356662423 12,162145639937194 12,341437186427655 12,53077035193341 12,549013699433756 12,590915568244977 12,864708139103053 13,475643525305873 13,491065447733362 13,712948699455504 13,87907526564229 13,93590629924399 14,108784530847219 14,212823360048446 14,589111140930992 14,590724454877103

5. Выполним статистическую обработку полученных результатов, для этого разделить заданный промежуток [T1; T2 ] на 24 равных интервала длиной:

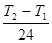
= , (мин). [T1 ; T2 ]= [8 ; 11 ].

Длина интервала ф = 0. 125.

Соответственно, сами интервалы образуют ряд:

8

8,125

8,125

8,25

8,25

8,375

8,375

8,5

8,5

8,625

8,625

8,75

8,75

8,875

8,875

9

9

9,125

9,125

9,25

9,25

9,375

9,375

9,5

9,5

9,625

9,625

9,75

9,75

9,875

9,875

10

10

10,125

10,125

10,25

10,25

10,375

10,375

10,5

10,5

10,625

10,625

10,75

10,75

10,875

10,875

11

Так как TK T2 , то из полученного массива TK выберем вектор, компоненты которого заключены в промежутке [8; 11]

TK1 = [8,191; 8,244; 8,377; 8,402; 8,497; 8,544; 8,660; 8,824; 9,052; 9,278; 9,331; 9,495; 9,579; 9,839; 9,889; 10,023; 10,043; 10,065; 10,137; 10,233; 10,247; 10,275; 10,335; 10,362; 10,419; 10,567; 10,737; 10,885; 10,971;].

Для каждого интервала определить x () - количество вызовов, попавших в интервал, длиной . Составляем и заполняем таблицу 2.

Таблица 2

№

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

X( )

0

2

0

3

1

1

1

0

1

0

2

1

1

0

5

1

3

3

3

1

1

1

0

2

Далее на основе данных таблицы 2 составляем таблицу 3, в которой первая строка определяет количество вызовов, попавших в интервал, длиной , А вторая строка определяет количество интервалов, в которое попало К вызовов

Таблица 3

X( )

0

1

2

3

Nk

6

11

3

4

N = NK = 24

NK - количество интервалов в которое попало К вызовов.

Получили таблицу 3 статистического распределения случайной величины, на основании которой определяем модельное значение параметра потока:

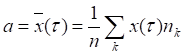
- мат. ожидание числа вызовов в К интервале.

А = (0*6+1*11+2*3+3*4)/24 = 1,208

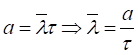
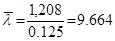
- модельное значение параметра потока

Контрольные вопросы.

1. По каким свойствам классифицируются случайные потоки?

Простейший поток обладает следующими свойствами:

    1. стационарность, 2. ординарность 3. отсутствие последействия. 2. Дать определение свойствам:

Стационарность;

Ординарность;

Отсутствие последействия.

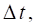
Стационарность потока означает, что с течением времени веро-ятностные характеристики потока не меняются. Поток можно назвать стационарным, если для любого числа K заявок, поступивших за промежуток времени длиной вероятность поступления требований зависит только от величины промежутка и не зависит от его расположения на оси времени.

,

Где - вероятность поступления K требований.

Ординарность означает, что события в потоке появляются по одиночке, а не группами. Поток требований можно назвать ординарным тогда, когда вероятность по-ступления двух или более требований за любой бесконечно малый промежуток времени есть величина бесконечно малая, более высокого порядка, чем, т. е.

.

Свойство Отсутствия последействия означает, что вероятность появления n событий на интервале ф не зависит от того, что произошло ранее интервала ф.

3. Дать определения числовым характеристикам случайных потоков:

Параметр потока ;

Интенсивность потока з;

Ведущая функция потока.

Ведущая функ-ция случайного потока - математическое ожидание чис-ла требований в промежутке [0, t). Функция - неотрицатель-ная, неубывающая, в практических задачах теории распределе-ния информации непрерывна и принимает только конечные значе-ния.

Параметр потока в момент времени T есть предел отно-шения вероятности поступления не менее одного требования в проме-жутке к величине этого промежутка при

.

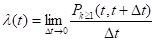
Интенсивность стационарного потока з есть математическое ожидание числа требований в единицу времени. Если интенсивность характеризует поток требований, то параметр - поток вызывающих моментов. Поэтому всегда з(t)?л(t), а равенство имеет место только для ординарных по-токов, когда в каждый вызывающий момент поступает только одно требование.

4. Для каких потоков совпадают значения параметра потока и интенсивности: = ?

Равенство имеет место только для ординарных по-токов, когда в каждый вызывающий момент поступает только одно требование.

5. По какому закону распределен промежуток между соседними вызовами в простейшем потоке?

Для простейшего потока заявок, длины промежутков времени между последовательными требованиями потока распределены по показательному закону с тем же параметром :

.

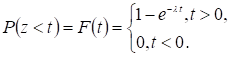
6. По какому закону распределена случайная величина, характеризующая количество вызовов простейшего потока, попавших в некоторый промежуток?

Для получения последовательности слу-чайных значений, распределенных по показательному закону с параметром, случайная величина, характеризующая количество вызовов простейшего потока, попавших в некоторый промежуток распределена по логарифмическому закону.

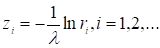
Похожие статьи




Моделирование простейшего потока заявок

Предыдущая | Следующая