Моделирование расчетных методов - Методы расчетов в платежных системах
В целях иллюстрации матричного моделирования расчетных методов используем практический числовой пример. Для отражения представленных в нем операций использованы расчеты между 5 участниками расчетов. По условиям задачи за период времени t1 - t2 по данным двадцати трех платежных инструкций, которыми обменивались пять участников расчетов (условно обозначаемых A, B, C, D, E), необходимо сформировать числовые выражения следующих моделей расчетных систем:
- -- валовых расчетов в режиме реального времени (Real-time Gross Settlement - RTGS); -- валовых расчетов с периодической (пакетной) обработкой платежей (Batch Gross Settlement - BGS); -- двухстороннего неттинга (Bilateral Netting - BN); -- многостороннего неттинга (multilateral netting - mn).
Транзакции в символическом виде при обработке платежных инструкций методом валовых расчетов в режиме реального времени могут быть записаны как:
RTGST2-t1 = 40E(А, B) + 80E(А, C) + 50E(А, D) + 30E(А, Е) + 70E(B, A) + 50E(B, C) + 40E(B, D) + 100E(B, Е) + 110E(C, A) + 40E(C, B) + 90E(C, D) + 60E(C, E) + 100E(D, A) + 120E(А, B) + 70E(D, C) + 140E(D, E) + 130E(E, A) + 20E(E, B) + 170E(E, C) + 30E(E, D) + 90E(A, B) + 190E(D, C) + 80E(B, D),
Где суммы, указанные в платежных инструкциях, умножены на соответствующие матрицы-корреспонденции и записаны в хронологическом порядке в течение периода обработки (t1 - t2). В общем виде метод валовых расчетов в режиме реального времени можно сформулировать следующим образом:
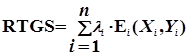
, (1)
Где коэффициентами линейного разложения являются скалярные величины -- суммы расчетных операций л i (i = 1, 2, ...), которые указаны в платежных инструкциях, а n -- равно их количеству.
Матричную формулу (1) мы называем информационно-технологическим образом системы Валовых расчетов в режиме реального времени: в ней суммы операций, определенные на соответствующих корреспонденциях между участниками расчетов, представлены в хронологическом порядке.
Заметим, что в течение периода обработки участник расчетов A три раза переводит средства участнику B, а участники D и B дважды передают расчетные активы соответственно участникам C и D, в то время как участник расчетов D не осуществляет переводов на участника B. Следовательно, числовое выражение формулы валовых расчетов с периодической обработкой платежей после приведения подобных матриц-транзакций будет иметь следующий вид:
BGST2-t1 = 250E(А, B) + 80E(А, C) + 50E(А, D) + 30E(А, Е) + 70E(B, A) + 50E(B, C) + 120E(B, D) + 100E(B, Е) + 110E(C, A) + 40E(C, B) + 90E(C, D) + 60E(C, E) + 100E(D, A) + 0E(D, B) + 260E(D, C) + 140E(D, E) + 130E(E, A) + 20E(E, B) + 170E(E, C) + 30E(E, D).
То есть переход от системы валовых расчетов в режиме реального времени к системе валовых расчетов с периодической обработкой платежей осуществляется путем "приведения подобных" (суммированием) матриц-транзакций за время периода обработки. Применив указанное преобразование, получаем формулу валовых расчетов с периодической обработкой платежей:
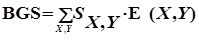
, (2)
Где коэффициентами линейного разложения будут суммы операций сводных расчетных операций: SX, Y (X, Y принадлежат множеству участников расчетов).
Приведение подобных матриц-транзакций за время периода обработки может выполняться по следующей формуле:
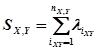
,
Где -- сумма единичной транзакции между участниками X И Y, а NX,Y -- количество транзакций между участниками X И Y в течение периода обработки платежей. Если в течение данного периода обработки расчеты между какими-либо участниками не проводились, то SX, Y = 0.
Матричная формула (2), на наш взгляд, является информационно-технологическим образом расчетов за определенный период обработки или системы Валовых расчетов с периодической обработкой платежей: в ней суммы (SX, Y) -- это итоговые суммы, состоящие из отдельных транзакций, определенных на однотипных корреспонденциях между участниками.
Для иллюстрации дальнейших преобразований систем расчетов запишем числовое выражение символического образа системы валовых расчетов с периодической обработкой платежей в матричном виде:
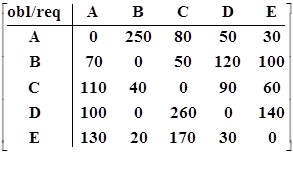
BGST2-t1 =.
Пусть BGS - это матрица обязательств между участниками расчетов, а
BGS = (BGS)
- транспонированная к ней матрица получаемых участниками платежей или матрица их требований, т. е. матрица, в которой строки и столбцы переставлены -- инвертированы по отношению к исходной матрице BGS. Для получения разницы между обязательствами (obligation - obl) и требованиями (requirement - req) необходимо из матрицы обязательств вычесть транспонированную к ней матрицу требований. Результатом этой операции будет матрица двухстороннего неттинга, представляющая собой разницу между требованиями и обязательствами, которая одновременно показывает направление перевода средств от плательщика к получателю для осуществления расчетов.
BNT2-t1 =
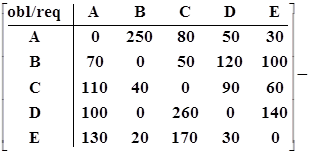
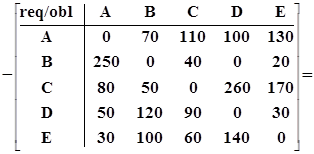
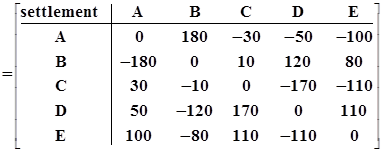
.
Обратите внимание на знаки чистой позиции, выраженные вектором-строкой: положительный и отрицательный. Как известно, знаки "-" (минус) и "+" (плюс) могут обозначать либо количество, либо действие. В данном случае при интерпретации знаков их следует воспринимать как знаки действия: "+" -- передача средств (откуда), "-" -- получение средств (куда).
Для перехода от системы валовых расчетов с периодической обработкой платежей к системе двухстороннего неттинга требуется из матрицы обязательств между участниками расчетов вычесть транспонированную к ней матрицу требований, результатом этих операций будет матрица двухстороннего зачета, формулу которой можно записать в следующем виде:
BN = BGS - BGS. (3)
Матрица BN обладает свойствами, в которых проявляется двойственная природа расчетных отношений:
1. Элементы сальдовой матрицы BN зеркально симметричны относительно главной диагонали, т. е. для каждого элемента S(X, Y) -- сальдо расчетов участников X и Y -- всегда существует равный по модулю, но противоположный по знаку элемент с инвертированной корреспонденцией S(Y, X) такой, что всегда соблюдается равенство:
S(X, Y) = - S(Y, X),
Где X, Y -- любые два корреспондирующих участника. Это свойство матрицы BN показывает двухсторонний зачет между участвующими в расчетах субъектами.
2. Поскольку сумма каждой пары зеркально симметричных элементов равна нулю, то и сумма всех элементов матрицы двухстороннего неттинга также равна нулю: S(X, Y)=0, т. е. все взаимные требования и обязательства урегулированы.
Матричная формула (3) -- это информационно-технологический Образ двухстороннего неттинга.
Свертывание матрицы обязательств, требований и двухстороннего зачета в итоговый столбец (вектор Векторы, в отличие от матриц, принято обозначать маленькими буквами.) достигается умножением справа на единичный вектор E (столбец, состоящий из единиц). Преобразование
Robl = BGSe
Сворачивает матрицу BGS в итоговый вектор обязательств, а преобразование
Rreq = BGSe
В итоговый вектор требований. По данным нашего примера, числовые значения преобразований запишутся в следующем виде:
RT2-t1obl =
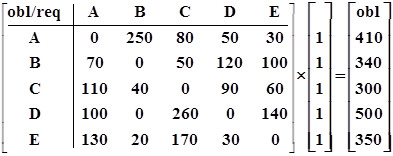
RT2-t1req =
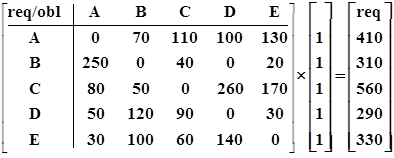
Числовое значение вектора чистых позиций после умножения матрицы двухстороннего зачета на единичный вектор может быть представлено в следующем виде:
Mnt2-t1 =
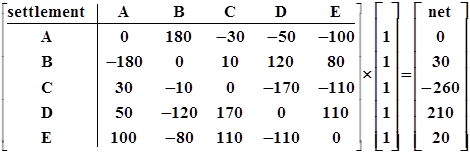
Отсюда следует, что для перехода от системы двухстороннего неттинга к системе многостороннего неттинга необходимо матрицу двухстороннего неттинга умножить на единичный вектор, результатом умножения являются многосторонние нетто-позиции каждого участника расчетов. На основании этого запишем формулу многостороннего неттинга в следующем виде:
Mn = BNe (4)
Векторная формула (4) -- это информационно-технологический образ Многостороннего неттинга. Его формула следует из матричных тождеств (1), (2) и (3).
Как известно, матрицу и вектор, содержащие положительные и отрицательные элементы, можно разложить на два объекта, один из которых будет положительным, а другой отрицательным. Для наглядности проведем это преобразование, тогда вектор многостороннего неттинга будет представлен следующим образом:
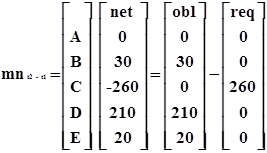
Обзор приведенного примера показывает, что для осуществления расчетов валовым методом требуется значительно больше средств по сравнению с системами нетто-расчетов. По данным нашей задачи видно, что, например, участнику расчетов А при проведении расчетов валовым способом требуются ликвидные средства в размере 410 единиц, а при проведении расчетов методом многостороннего неттинга он имеет нулевую нетто-позицию. При осуществлении расчетов на основе двухстороннего неттинга между участниками A и B вместо 250 единиц расчетных активов участнику А требуется всего 180, а участник B вообще не затрачивает средств для осуществления двухсторонних расчетов. Кроме этого, средства, необходимые для расчетов между всеми участниками при сравнении системы валовых расчетов и системы многостороннего неттинга расчетов, снижаются с 1900 (сумма обязательств всех участников) единиц расчетных активов до 260.
Смешанные системы являются частным случаем систем нетто-расчетов и моделируются путем последовательных преобразований системы брутто-расчетов, причем эти преобразования могут завершиться либо двухсторонним зачетом, либо многосторонним неттингом. Например, в России в настоящее время введена в эксплуатацию система банковских электронных срочных платежей (БЭСП), которая позволяет ее участникам рассчитываться как валовым методом, так и на основе двухстороннего взаимозачета. В системе БЭСП предусматривается также и взаимозачет электронных платежных сообщений на многосторонней основе, однако процедура расчета методом многостороннего неттинга пока не разъяснена в нормативных документах.
Содержательный результат формульного представления моделей расчетов заключается в том, что удалось перейти от обычного процедурного описания технологии расчетов к ее представлению в форме компактных и единообразных матричных тождеств. Основные методы расчетов представлены как система следующих друг из друга компактных векторно-матричных формул, которые могут быть полезны для единообразного понимания расчетных взаимоотношений. Кроме этого, приведенная система матричных моделей обеспечивает единство методологических подходов с системой информационно-технологических образов операций бухгалтерского учета в системе ситуационно-матричной бухгалтерии, что является очень важным, так как расчетные операции и система учета этих операций в балансах организаций, по нашему мнению, взаимосвязаны.
Обычно в основу аналитических выводов при обосновании правильности функционирования платежных систем, как правило, закладывается опыт представителей этих систем. Однако основные выводы, базой которых является практический опыт и так называемый здравый смысл, в противоположность выводам логики и математики, являются только формой понимания представителями конкретных экономических сообществ правильности функционирования платежных систем. Практический опыт зависит от социально-экономических условий и исторических традиций, в рамках которых он приобретен, и поэтому не может быть напрямую заимствован, а затем использован в тех странах, где упомянутые условия и традиции имеют принципиальные отличия.
Язык математики, как показывает вся история развития науки, обладает необходимым единообразием в понимании и большей общностью в логических рассуждениях и выводах, чем профессиональный язык, близкий к естественному. Поэтому язык математики имеет перспективу быть одинаково понятным в разных странах.
В последнее время в отечественных публикациях очень много внимания уделяется опыту функционирования платежных систем в экономически развитых странах. Это увлечение зарубежными разработками понятно, поскольку при построении платежных систем хочется использовать передовую практику. Однако представляется, что простое подражание -- не лучший способ интеграции в мировое экономическое сообщество. Кроме этого, следует помнить, что при копировании зарубежного опыта функционирования платежных систем отечественные системы неизбежно будут отставать от западных, так как функционирующие в настоящее время системы -- результат научно-технических решений прошлых лет. Поэтому для разработки новых систем перевода средств, расчетов и платежей необходимо не только использовать передовую зарубежную практику, но и учитывать направления будущего развития. В связи с этим, математическое моделирование расчетных методов может дать конкурентные преимущества при конструировании новейших платежных систем, разрабатываемых в России.
Похожие статьи
-
Валовые и нетто-расчеты - Методы расчетов в платежных системах
При всем многообразии классификационных признаков, по которым различают платежные системы, для совершения расчетов в этих системах используются только...
-
Моделирование расчетных взаимоотношений в платежных системах - Методы расчетов в платежных системах
Модель (французское modиle, от латинского modulus -- мера, образец) -- описание объекта (предмета, процесса или явления) на каком-либо формализованном...
-
Понятие расчетного механизма Уверенность в надежности и безопасности системы платежей имеют решающее значении, указанные критерии исключают возможность...
-
Во второй главе мне бы хотелось рассмотреть и изучить современную банковскую платежную систему, описать ее основные функции и качества. В разделах данной...
-
Классификация ЭПС - Электронные платежные системы
Платежные системы можно классифицировать по следующим признакам: По иерархии, или степени подчинения. Различаются системы централизованные (древовидные),...
-
При осуществлении платежей возникают ситуации, связанные с возможностью потери части или всех средств при их перемещении от плательщика к получателю....
-
Роль банковских пластиковых карт в системе безналичных расчетов, история развития, виды и классификация карт В повседневной жизни оплата наличными...
-
Участники ЭПС, Требования к платежным системам - Электронные платежные системы
Рисунок 2 - Участники электронных платежей Обычно банки исполняют в платежных протоколах две роли: эмитента (взаимодействующего с плательщиком) и...
-
Перспективы развития платежных систем в мире - Банковская система в Великобритании
В данном параграфе мне бы хотелось проанализировать перспективы развития платежных систем в мире. Мой обзор будет сфокусирован на основных ведущих...
-
Одним из последних банковских продуктов является услуга "Интернет-банкинг". Повсеместное распространение вычислительной техники и распространение...
-
Расчет экономической эффективности по переводам и платежам банка относится к категории сложных и комплексных экономических задач, должны рассматриваться...
-
Анализ динамики и структуры использования пластиковых карт в Казахстане Люди уже привыкли к виду карточки в своем портмоне. Банковские карточки уже около...
-
Электронные платежные системы как современное средство расчетов, их преимущества и недостатки Чрезвычайно скорое развитие всемирной сети "Интернет" стало...
-
Действующая в республике система безналичных расчетов позволяет клиентам банков осуществлять расчеты с использованием различных платежных инструментов....
-
Для того чтобы обозначит роль банковских карт в платежной системе, дадим определение понятию "платежная система". Платежная система - это совокупность...
-
Пластиковая карточка - это персонифицированный платежный документ, предоставляющий владельцу возможность безналичной оплаты товаров и услуг, а также...
-
Условия исполнения банком платежного поручения - Содержание расчетов посредством платежных поручений
Платежные поручения препровождаются в банк на бланке определенной формы и обязаны включать: - название расчетного документа; - номер платежного...
-
Расчеты платежными поручениями - Расчеты платежными поручениями
Это - самая распространенная в настоящее время в России форма безналичных расчетов. Платежное поручение представляет собой поручение предприятия...
-
Пути совершенствования безналичных расчетов и пластиковых карт Сегодня, с большинством проблем, наши банки в основном справились. Однако далеко не все...
-
Банкоматы (АТМ - Automated Teller Machine) - это многофункциональные автоматы, так называемые автобанки, управляемые последним поколением магнитных...
-
Началом процесса формирования официальных рекомендаций о принципах функционирования и управления системами расчетов и платежей можно считать работу...
-
В целях снижения риска мошенничества с использованием платежных карточек при осуществлении безналичных расчетов казахстанскими банками проводится ряд...
-
Общие положения о расчетах платежными поручениями Расчеты платежными поручениями - это наиболее часто употребляемая в имущественном выражении...
-
Система безналичных расчетов в Российской Федерации представляет собой совокупность государственных законов и правил, регулирующих механизм организации...
-
Особенности исполнения платежного поручения - Содержание расчетов посредством платежных поручений
Непосредственно реализация платежного поручения плательщика заключается в том, что принявший его банк должен перечислить показанную в поручении сумму...
-
Развитие клиринговой системы Развитие клиринговой системы в Казахстане началось в 1995 году. На начальной стадии внедрения клиринга в Казахстане операции...
-
Внедрение прогрессивных форм и методов работы с пластиковыми картами В Казахстане создана концепция автоматизированной системы безналичных платежей и...
-
Межбанковские расчеты возникают в том случае, когда плательщик и получатель средств имеют счета в разных банках, а также при взаимном кредитовании...
-
Наиболее перспективной и получающей все большее развитие становится форма электронных расчетов посредством платежных карт и электронных денег. Стратегия...
-
Международные безналичные расчеты - Содержание расчетов посредством платежных поручений
В процессе межгосударственного сотрудничества и воплощение в жизнь разнообразных торгово-экономических договоров, контрактов и программ, а также...
-
Понятие и формы безналичных расчетов Экономика любого государства представляет собой широко разветвленную сеть различных хозяйствующих субъектов. Основой...
-
Понятие и законодательное регулирование безналичных расчетов Термин "система расчетов" определяется как система, где осуществляются операции, в...
-
АО "Народный Банк Казахстана" эффективно использует в своей деятельности S. W.O. T. - анализ для оценки платежных инструментов так как совершенствование...
-
Проблемы и перспективы развития инструментов платежей и расчетов в АО "Народный банк Казахстана" На данный момент в Республики Казахстан расчеты...
-
В самом общем виде инфраструктура, поддерживающая работу с платежными картами, выглядит следующим образом: - Центральный административный орган -...
-
Заключение - Содержание расчетов посредством платежных поручений
В заключение хотелось бы определить основные задачи, условия их решения и меры по их реализации для создания высокоэффективной платежной системы, что...
-
Вопрос. Правовое регулирование расчетов платежными поручениями и чеками - Банковское право
Платежное поручение - это форма безналичных расчетов, по которой банк плательщика обязуется осуществить перевод денежных средств по его (плательщика)...
-
Понятие и экономическое значение безналичных расчетов в современном денежном обороте РК Выполнение банками функции безналичных расчетов связано, прежде...
-
Сбербанк России обслуживает все группы корпоративных клиентов. На долю малых и средних компаний приходится более 33,9% корпоративного кредитного...
-
Формы безналичных расчетов и их характеристика - Анализ системы безналичных расчетов
Согласно Гражданскому кодексу в Российской Федерации при осуществлении безналичных расчетов "допускаются расчеты платежными поручениями, по аккредитиву,...
Моделирование расчетных методов - Методы расчетов в платежных системах