Численные методы анализа
Задание 1
Гаусс mathcad интерполяция
Найти сумму (разность) приближенных чисел и указать ее погрешности (Д и д), если считать в исходных данных все значащие цифры верными:
.
Решение.
По условию:
, , ,
, , .
Вычисляем выражение:
.
Вычисляем абсолютную погрешность:
.
Относительная погрешность:
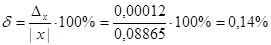
Ответ. , , .
Задание 2
Найти решение СЛАУ, где - матрица коэффициентов, - вектор свободных членов, - вектор неизвестных, методом Гаусса с выбором главного элемента по столбцу. Заданы матрица и вектор. При поиске решения (в MathCAD) показать все промежуточные вычисления в прямом и обратном ходе указанных прямых методов. Полученное (приближенное) решение сравнить с решением этой СЛАУ в MathCAD вычислительным блоком Given...find (расчет провести в численном виде). Зарисовать блок-схему алгоритма указанного в варианте метода решения СЛАУ при условии произвольного количества уравнений (задаются матрица и вектор ).
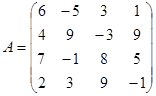
,
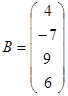
Решение.
Решение задачи в MathCAD с помощью блока Given..Find:

Блок-схема алгоритма - решение СЛАУ методом Гаусса с выбором главного элемента по столбцу:
- функция, с помощью которой выбираем главный элемент по столбцу и меняем строки:
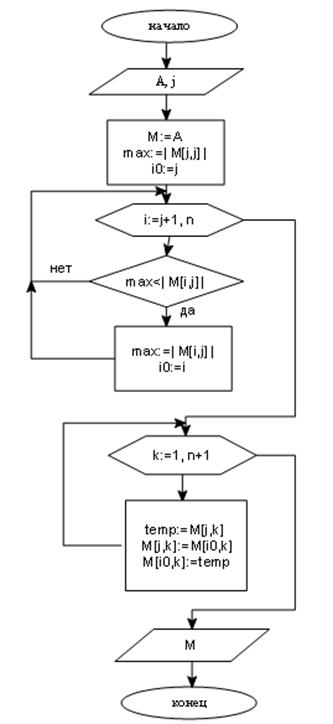
- функция прямого хода метода Гаусса () и обратный ход метода Гаусса ():
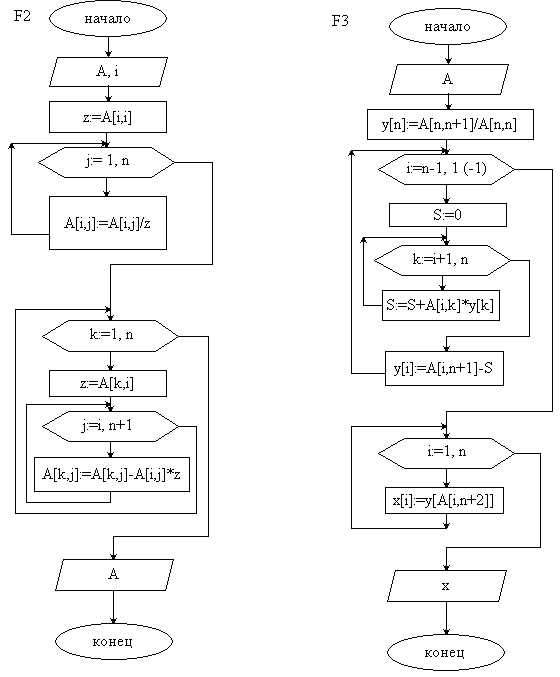
- главная программа:
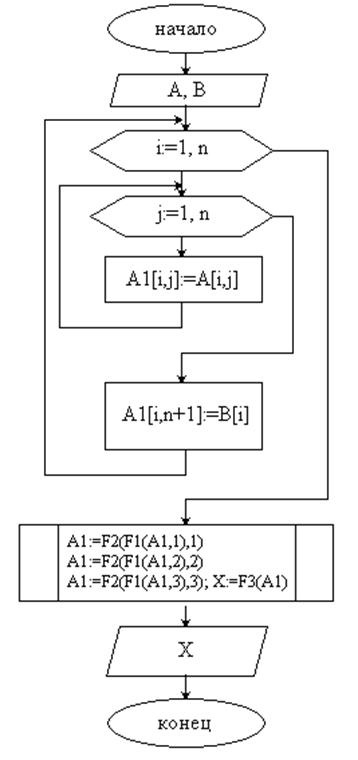


Последовательность вычислений:

Задание 3
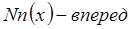
По заданным узловым значениям исходной функции (векторы и ) осуществить интерполяцию - интерполяционным полиномом Ньютона.
Построить в MathCAD в одном графическом шаблоне полученный интерполяционный полином и узловые значения исходной функции.
Зарисовать блок-схему алгоритма, реализующего вычисление значения интерполяционного полинома Лагранжа в любом значении аргумента при условии произвольного количества узловых значений исходной функции.
По заданным узловым значениям исходной функции (векторы и ) записать систему линейных алгебраических уравнений для расчета коэффициентов кубического сплайна со свободным закреплением концов, решить эту систему в MathCAD вычислительным блоком Given...find, записать функцию, реализующую рассчитанный кубический сплайн, считая, что за границами рассматриваемого диапазона изменения аргумента изменение функции осуществляется соответственно по начальному и конечному частям сплайна. Построить в одном графическом шаблоне рассчитанный кубический сплайн и узловые значения исходной функции.
По заданным узловым значениям исходной функции (векторы и ) методом наименьших квадратов определить коэффициенты аппроксимирующего обобщенного многочлена, где цk - система базисных функций (в задании даны степенные функции). Согласно методу наименьших квадратов коэффициенты определяются из условия
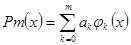
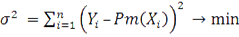
(1)
При поиске минимального значения необходимое и достаточное условие:
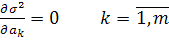
(2)
Дает систему из линейных алгебраических уравнений относительно неизвестных. Записать систему (2) и решить ее в MathCAD вычислительным блоком Given...find, отобразить в одном графическом шаблоне полученный аппроксимирующий обобщенный многочлен и узловые значения исходной функции. Рассчитать величину для полученного аппроксимирующего обобщенного многочлена.
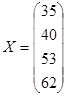
, , ,
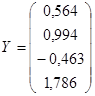
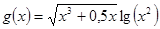
, , , , logfit
Решение.
Строим интерполяционный полином Ньютона (вид записи - интерполяция вперед):
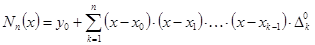
.
Разделенными разностями первого порядка, составленными по соседним узлам, называют отношения
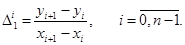
По ним можно определить разделенные разности второго порядка
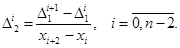
Аналогично определяются разделенные разности более высокого порядка. Например, если известны разделенные разности - го порядка, то разделенная разность - го порядка определяется как
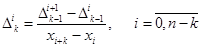
.
Вычисления производим в MathCAD:
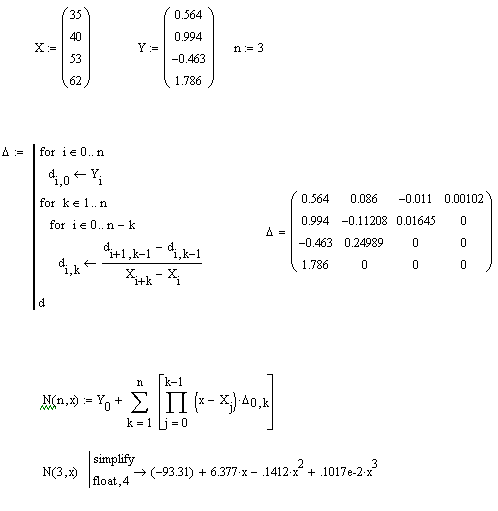
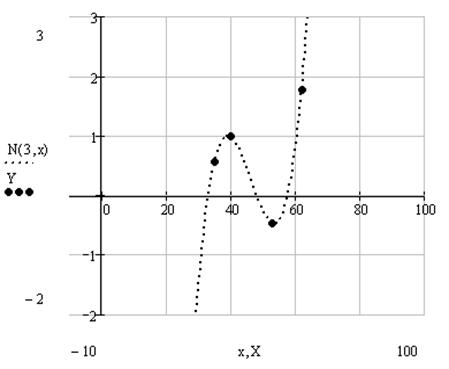
Построим в MathCAD в одном графическом шаблоне полученный интерполяционный полином и узловые значения исходной функции.
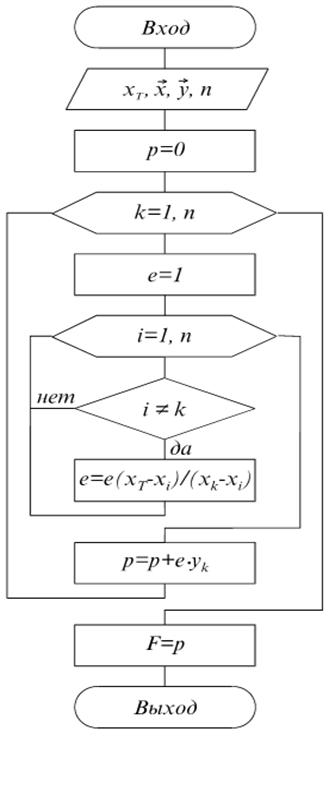
Блок-схема алгоритма, реализующего вычисление значения интерполяционного полинома Лагранжа в любом значении аргумента XT при условии произвольного количества узловых значений исходной функции:
По заданным узловым значениям исходной функции (векторы и ) запишем СЛАУ для расчета коэффициентов кубического сплайна со свободным закреплением концов.
Известно, что при кубическом сплайне между парой соседних узлов интерполяции имеем кубический многочлен вида
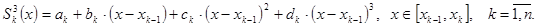
Для определения коэффициентов, , , на всех отрезках записывают и решают линейных уравнений из условия непрерывности функции
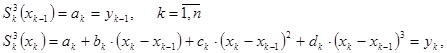
Непрерывности первых и вторых производных в узлах интерполяции
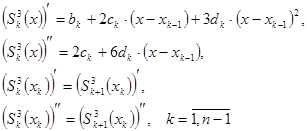
И условия свободного закрепления концов
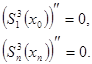
В нашем случае имеем:

Решаем эту систему в MathCAD вычислительным блоком Given...find:
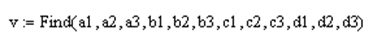
Получаем:

Запишем функцию, реализующую рассчитанный кубический сплайн, считая, что за границами рассматриваемого диапазона изменения аргумента изменение функции осуществляется соответственно по начальному и конечному частям сплайна:
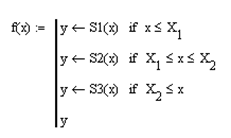
Построим в одном графическом шаблоне рассчитанный кубический сплайн и узловые значения исходной функции:
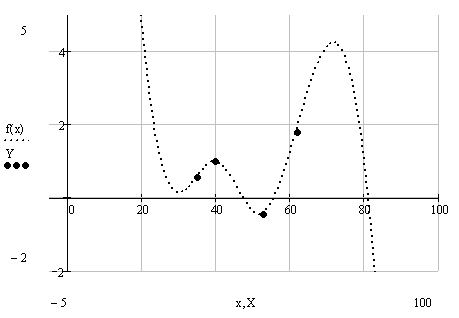
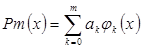
По заданным узловым значениям исходной функции (векторы и ) методом наименьших квадратов определим коэффициенты аппроксимирующего обобщенного многочлена, где - система базисных функций (в задании даны степенные функции). Согласно метода наименьших квадратов коэффициенты определяются из условия
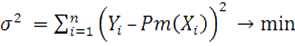
. (1)
При поиске минимального значения необходимое и достаточное условие
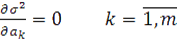
(2)
Дает систему из линейных алгебраических уравнений относительно неизвестных.
Запишем систему (2) и решим ее в MathCAD вычислительным блоком Given...find.
Экстремальная задача примет вид:
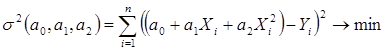
.
Параметры искомой зависимости находятся из системы:
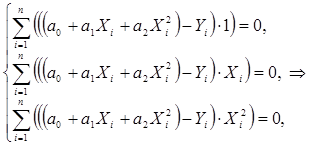
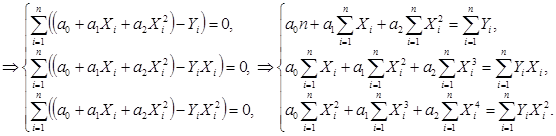

Отобразим в одном графическом шаблоне полученный аппроксимирующий обобщенный многочлен и узловые значения исходной функции:
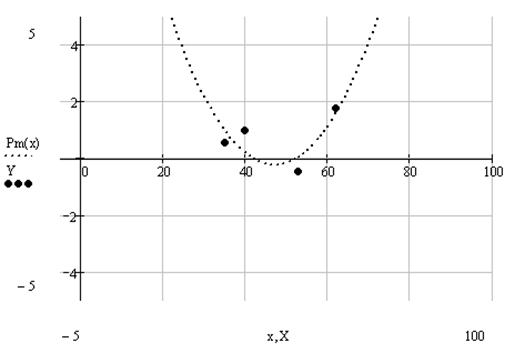
Величина для полученного аппроксимирующего обобщенного многочлена:
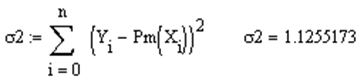
А) Реализуем в MathCAD по рассчитанным узловым значениям (векторы и ) кусочно-линейную интерполяцию (функция linterp), кубическую сплайновую с различным продолжением (функции lspline, pspline, cspline, interp). Отобразим в одном графическом шаблоне исходную функцию, узловые значения (векторы и ) и четыре полученные интерполяционные функции.

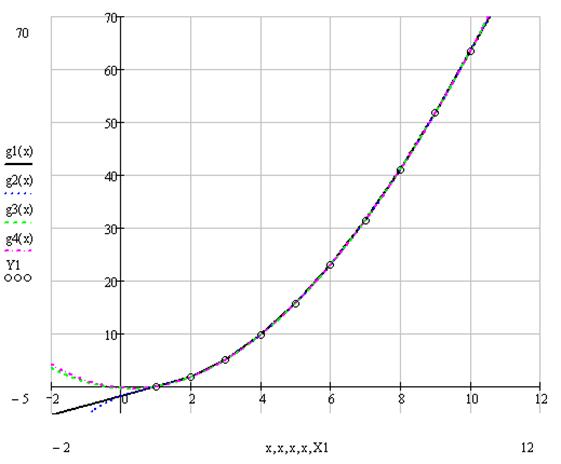
Б) По узловым значениям (векторы и ) реализовать в MathCAD В-сплайн интерполяцию с различными степенями заменяющих полиномов (), выбрав самостоятельно векторы точек сшивок. В одном графическом шаблоне отобразить исходную функцию, узловые значения (векторы и ), три интерполяционные функции В-сплайнов и соответствующие им точки сшивок.

Графики:
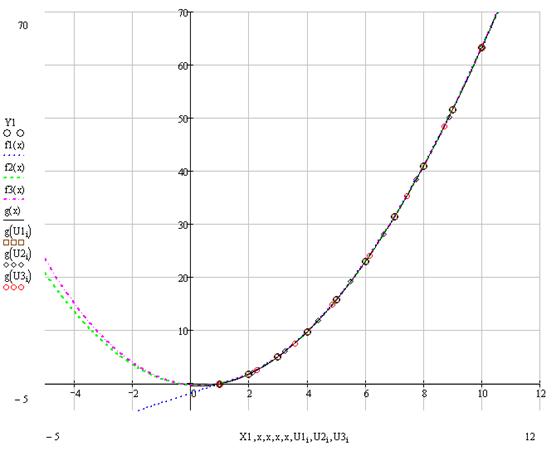
В) По узловым значениям (векторы и ) реализуем в MathCAD линейную аппроксимацию (функции line, medfit), полиномиальную аппроксимацию (функции regress (в задании даны степени аппроксимирующих полиномов) и loess (параметр span выбрать самостоятельно)), аппроксимацию функциями специального вида (в задании указана одна из функций expfit, lgsfit, sinfit, pwfit, logfit, lnfit).
Для всех аппроксимирующих функций рассчитаем величину среднеквадратичного отклонения ().
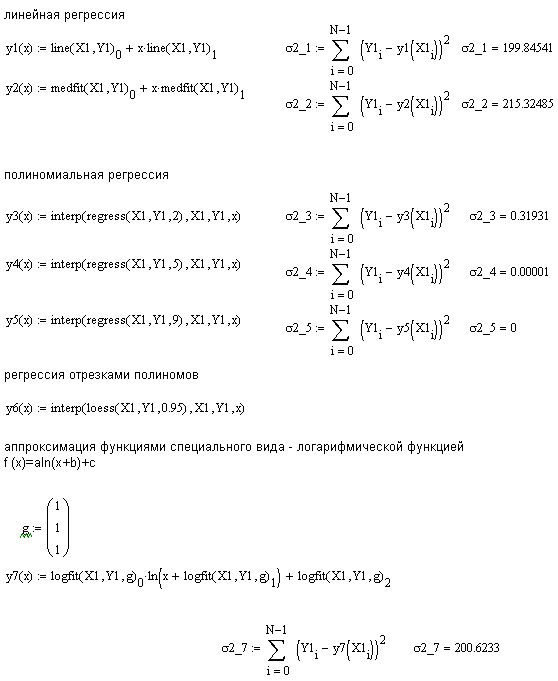
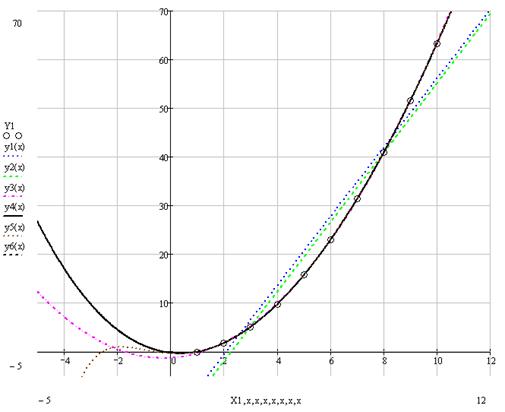
Отобразим в одном графическом шаблоне исходную функцию, узловые значения (векторы и ) и полученные аппроксимирующие функции.
Задание 4
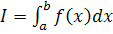
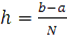
В MathCAD вычислить интеграл методом трапеций при заданном количестве разбиений интервала интегрирования (шаг интегрирования ) и оценить погрешность применения данной составной квадратурной формулы для вычисления интеграла.
Для вычисления интеграла по указанному методу написать функцию пользователя, в которой входным параметром является количество разбиений интервала интегрирования. Отобразить функции, и (в соответствии с применяемыми методами) на интервале.
, ,
Решение.
Разбиение интервала задается следующим образом:
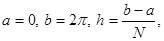
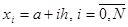
.
Для вычисления интеграла методом трапеций воспользуемся формулой:
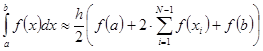
.
Составим в MathCAD функцию пользователя и вычислим интеграл при разных количествах разбиений:
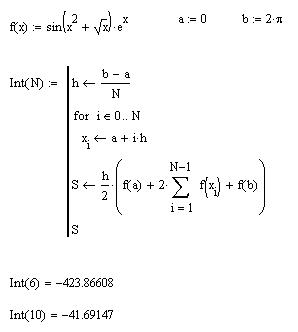
В методе трапеций в соответствии с оценкой остаточного члена формулы для вычисления интеграла - оценка погрешности
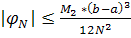
, где.
Вычисляем максимальное значение модуля второй производной на данном отрезке:
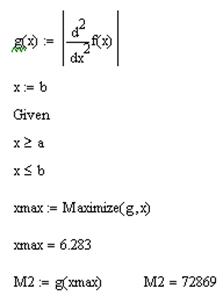
Оценки погрешности для каждого :
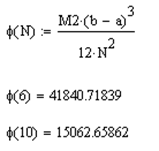
Строим графики функций и :
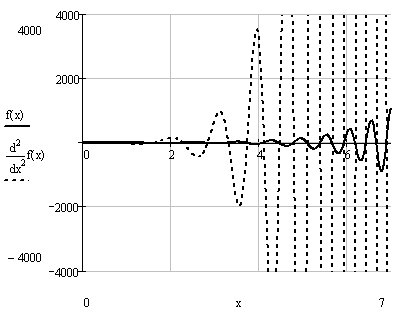
Находим необходимое количество интервалов для достижения заданной точности:
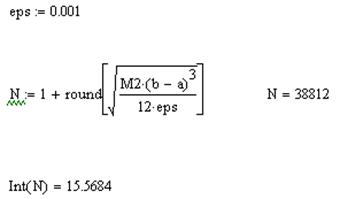
Литература
- 1. Электронный учебно-методический комплекс по дисциплине "ЧИСЛЕННЫЕ МЕТОДЫ АНАЛИЗА" для специальностей: 1-45 01 01 "Многоканальные системы телекоммуникаций"..., БГУИР - 2012. 2. Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. - М.: Бином, 2006. 3. Самарский А. А. Введение в численные методы. - М.: Лань, 2009. 4. Крылов В. И. Вычислительные методы / В. И. Крылов, В. В. Бобков, П. И. Монастырный - М.: Наука, 1976, т. 1 5. Крылов В. И. Вычислительные методы / В. И. Крылов, В. В. Бобков, П. И. Монастырный - М.: Наука, 1977, т. 2 6. Черняк А. А., Черняк Ж. А., Доманова Ю. А. Высшая математика на базе MathCad. Общий курс. - СПб.: БХВ Петербург, 2005.
Похожие статьи
-
Методы анализа политических процессов - Методы анализа национальной экономики
Все методы анализа политических процессов можно разделить на две большие группы: количественные и качественные. К первой относятся статистический и...
-
Понятие, цели и методы приватизации Приватизация является близким по значению словом к понятию "разгосударствление". Касаясь субординации категорий...
-
Регрессионный анализ как продуктивный метод исследования статистических данных
РЕГРЕССИОННЫЙ АНАЛИЗ КАК ПРОДУКТИВНЫЙ МЕТОД ИССЛЕДОВАНИЯ СТАТИСТИЧЕСКИХ ДАННЫХ В данной статье рассматривается регрессионный анализ как эффективный метод...
-
На каждом из этапов стратегического процесса за основу берутся определенные подходы. На первых двух стадиях используются такие методы, как PEST-анализ,...
-
Метод группировки и его место в системе статистических методов Группировка статистический индекс выборочный Различные единицы статистической...
-
Показатели учета национального производства - Методы анализа национальной экономики
Сотни тысяч фирм, миллионы граждан, государственные органы в своей деятельности принимают решения о сотнях миллионов разнообразных сделок. Однако на...
-
Введение - Методы анализа национальной экономики
Актуальность темы данной курсовой работы велика в связи с важностью исследований по выбранной теме для внедрения полученных результатов в экономическую...
-
Итак, модели, которые будут дальше анализироваться, и получены с помощью первого метода - проведения теста для выделения наиболее дескриптивных...
-
Синтетические свойства индексов состоят в том, что посредством индексного метода производится соединение (агретрование) в целое разнородных единиц...
-
Традиционный метод прямого вычисления себестоимости (директ-костинг) основан на вычитании прямых расходов из продажной выручки и определении предельной...
-
Для оценки планирования производительности труда используются следующие методы: натуральный, трудовой и стоимостной. Рисунок 2 - краткая характеристика...
-
Потребности в экономическом анализе существуют всегда, независимо от вида экономических отношений, складывающихся в обществе, но акценты, делающиеся в...
-
Показатели выражения определенных функций управления в системе государственного регулирования экономики, диапазон их применения, а также возможности их...
-
Отбор единиц при использовании собственно-случайной выборки предполагает непреднамеренный отбор единиц генеральной совокупности в выборочную. При этом...
-
Понятие о выборочном наблюдении Первым этапом статистического наблюдения является наблюдение. Этот этап может осуществляться сплошным и несплошным...
-
Система национального хозяйства страны - Методы анализа национальной экономики
Целостная система экономики страны включает производство, распределение, обмен и потребление продукции (экономических благ). Предложение и реализация...
-
При расчете сводных индексов при сравнении показателей за два периода могут использоваться веса как текущего, так и базисного уровня. Если индексы...
-
Одной из задач, возникающих при анализе рядов динамики, является установление закономерности изменения уровней изучаемого показателя во времени. В...
-
Аналитические группировки обеспечивают установление взаимосвязи и взаимозависимости между исследуемыми социально-экономическими явлениями и признаками,...
-
Производительность труда - показатель динамичный, постоянно изменяется под воздействием множества факторов. Все факторы, воздействующие на...
-
Метод экономического анализа ABC-анализ - Метод экономического анализа АВС-анализ
Современный период стремительных изменений и перехода в новое становление обусловлен всевозрастающей конкурентной борьбой, которая диктует организацию...
-
Весьма часто предприятие сталкивается с ситуацией, когда имеется ряд альтернативных (взаимоисключающих) инвестиционных проектов. Естественно, возникает...
-
Выбирая тот или иной метод оценки израсходованных материалов, можно влиять и на себестоимость продукции, и на размер налогооблагаемой прибыли. Именно...
-
Использование статистических показателей в дисперсионном анализе
Задача 1 По территориям Волго-Вятского, Центрально-Черноземного и Поволжского районов известны данные: Район Потребительские расходы в расчете на душу...
-
В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решений. Для...
-
Исходя из того, что объектом изучения логистики являются материальные, денежные, информационные, энергетические и другие потоки, в процессе управления...
-
Средние величины представлют собой наиболее распространенную форму сводных величин. Они дают общую количественную характеристику элементов массового...
-
Классификация методов экономической оценки эффективности инвестиций Инвестиции -- важнейший и наиболее дефицитный экономический ресурс, использование...
-
Понятие о статистических рядах динамики Методы анализа рядов динамики занимают немаловажное место в связи с тем, что уровни общественных явлений...
-
По источникам формирования оборотные средства предприятия подразделяются на собственные и заемные. Процесс разработки экономически обоснованных величин...
-
Традиционно ABC-анализ проводится в три этапа - Метод экономического анализа АВС-анализ
Этап 1 . Определение объекта анализа и параметров его Оценки . В качестве объекта анализа могут выступать: Ш товарные группы; Ш Товарные категории ; Ш...
-
Структурные группировки разделяют однородную в качественном отношении совокупность единиц по определенным, существенным признакам на группы,...
-
Заключение - Методы анализа национальной экономики
В ходе проведенной научно-исследовательской работы, поставленные во введении Цели, достигнуты, задачи выполнены . Рассмотрев сущность и основы...
-
Типологическая группировка представляет собой разделение исследуемой качественно разнородной статистической совокупности на классы,...
-
Основные черты метода сбора данных Развитие эмпирических методов изучения экономических явлений обусловило определенные предпосылки для анализа...
-
Статистика как наука имеет свой предмет исследования. Она изучает с количественной стороны в непосредственной связи с качественным содержанием массовые...
-
Наряду со случайным отбором применяется механический отбор. При этом способе генеральная совокупность делится на столько групп, сколько единиц наблюдения...
-
Различные подходы к анализу экономической динамики - Предмет и методы экономической теории
В науке к настоящему времени сложились два подхода в анализе экономической динамики и статики: анализ с учетом воспроизводственного подхода и...
-
Введение - Применение статистических методов при анализе динамических процессов и явлений
Анализ и обобщение статистических данных - заключительный этап статистического исследования, конечной целью которого является полчение теоретических...
-
Так как мы рассматриваем тему распределение, то нам еще следует проанализировать рынки сбыта, каналы сбыта и структуру оптового товарооборота. Территория...
Численные методы анализа