Статистическая обработка исходных данных - Проектирование автоматизированной системы резервирования мест и продажи билетов на автовокзале
Так как объем статистической выборки достаточно велик (n=365), статистическая обработка осуществляется с помощью метода группирования.
Одним из возможных алгоритмов расчета характеристик эмпирического распределения непрерывной случайной величины является следующий:
- А) по результатам наблюдения (замеров) необходимо получить заданное число n значений исследуемого параметра для процесса, явления, предмета; Б) составить интегральные статистические ряды распределения частот и частостей полученных значений случайной величины:
- 1) найти минимальное и максимальное значения случайной величины и размах варьирования
XР= XMax - XMin; (2.1)
XР= 9992 - 1569 = 8423 т.
2) определить число интервалов N разбиения случайной величины. Количество рядов, на которые разделяется выборка определяется по формуле Стерджесса:
NП = 1 + 3,32 * lg n; (2.2)
Где n - размер выборки случайной величины;
N = max(NП;5), (2.3)
NП = 1 + 3,32 * lg 365 = 9.51.
Количество разрядов принимается равным 9.
N = max(9;5)=9.
3) рассчитать длину интервала h
H = XР / N; (2.4)
H = 8423 / 9 = 935,89.
Длина разряда принимается равной 936.
4) определить границы XJ (верхнюю), XJ-1(нижнюю) и середину XСj j-го интервала случайной величины (j=1...N)
XJ = XMin + jh; (2.5)
XJ-1 = XMin + (j - 1)h; (2.6)
XСj = (XJ-1 + XJ)/2. (2.7)
Определяется середина первого интервала, а так же его верхняя и нижняя граница:
XJ = 1569 + 1*936 = 2505; XJ-1 = 1569 + (1 - 1)936 = 1569;
XСj = (1569 + 2505)/2 = 2037.
Для остальных интервалов расчет сведен в таблицу 2.1.
Таблица 2.1 Расчет границ и середин интервалов распределения случайной величины
|
Интервал j |
Граница |
Середина Xсj | |
|
Верхняя Xj |
Нижняя Xj-1 | ||
|
1 |
2505 |
1569 |
2037 |
|
2 |
3441 |
2505 |
2973 |
|
3 |
4377 |
3441 |
3909 |
|
4 |
5313 |
4377 |
4875 |
|
5 |
6249 |
5313 |
5781 |
|
6 |
7185 |
6249 |
6717 |
|
7 |
8121 |
7185 |
7653 |
|
8 |
9057 |
8121 |
8589 |
|
9 |
9993 |
9057 |
9525 |
5) подсчитать число попаданий случайной величины в каждый j-й интервал (частоты MJ), для чего пересмотреть все числа xI (i = 1...n) относительно границ интервалов
MJ = MJ + 1 , если XJ-1 ? хI < XJ при j = 1...N-1;
MJ = MJ + 1 , если XJ-1 ? хI ? XJ при j = 1...N;
6) определить частости (эмпирические вероятности) рЭj появления значений случайной величины в каждом из интервалов путем деления соответствующих частот на объем выборки n, т. е. рЭj = MJ / n. Сумма всех частот равна объему выборки

(2.8)
А сумма частостей рЭj соответственно равна единице.
Частоты и частости появления значений случайной величины в каждом из интервалов представлены в таблице 2.2.
Таблица 2.2 Частоты и частости появления значений случайной величины в каждом из интервалов
|
Номер интервала j |
Частоты Mj |
Частости рэj |
|
1 |
10 |
0,0274 |
|
2 |
46 |
0,1260 |
|
3 |
93 |
0,2548 |
|
4 |
113 |
0,3096 |
|
5 |
69 |
0,1890 |
|
6 |
26 |
0,0712 |
|
7 |
6 |
0,0164 |
|
8 |
1 |
0,0027 |
|
9 |
1 |
0,0027 |
|
Сумма |
365 |
1 |
В) построить гистограмму или полигон эмпирического распределения.
С этой целью строят график, на котором по оси Х откладывают границы интервалов значений случайной величины. На каждом из интервалов строится прямоугольник, высота которого равна частному от деления частости данного интервала на величину интервала:
FЭj = рЭj / h, (2.9)
Где fЭj - эмпирическая функция плотности вероятности.
Полигон строится также по значениям fЭj, но на серединах интервалов в виде ломаной линии.
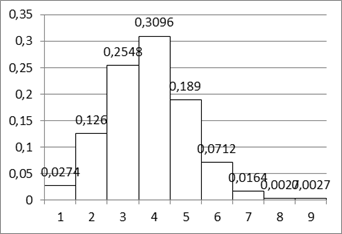
Рисунок 2.1 Гистограмма эмпирического распределения суточных объемов перевозок
Г) определить значения функции распределения и построить для нее график

При этом FЭ0 = 0 (j=0).
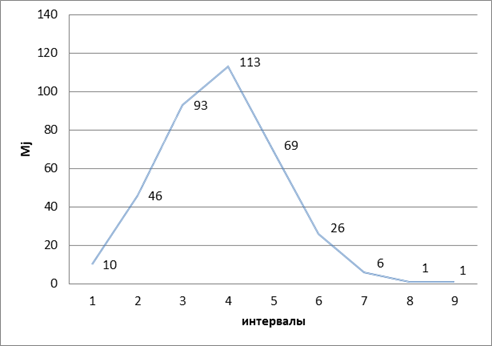
Рисунок 2.2 Полигон эмпирического распределения
Д) определить числовые характеристики выборки: начальные µK и центральные статистические µCk моменты k-го порядка и рассчитываемые через них параметры (оценка среднего арифметического xM, выборочная дисперсия s2, среднеквадратическое отклонение s, коэффициент вариации V, асимметрия А и эксцесс Е)


Или ; (2.11)
XМ= µ1 ; (2.12)


Или ; (2.13)
S2 = kCµCk; (2.14)

S = ; (2.15)
V = s/ xМ. (2.16)
Статистические характеристики выборки представлены в таблице 2.3.
Таблица 2.3 Статистические характеристики выборки
|
Показатель |
Значение |
|
Медиана |
4670 |
|
Мода |
4726 |
|
Стандартное отклонение |
1177,97 |
|
Дисперсия выборки |
1387610 |
|
Эксцесс |
0,844 |
|
Минимум |
1569 |
|
Максимум |
9992 |
|
Сумма |
1684220 |
|
Размах выборки |
365 |
|
Ассиметричность |
0,317 |
Гипотеза о законе распределения исследуемой случайной величины выдвигается на основании учета следующих данных:
Условия и факторы, влияющие на процесс формирования значений случайной величины; форма гистограммы (полигона); значения коэффициента вариации V.
Исходя из формы гистограммы, а также из того, коэффициент вариации равен 0,115, можно выдвинуть гипотезу о том, что распределение посуточного объема перевозки подчиняется нормальному закону.
Для выбранного закона распределения необходимо определить значения его параметров, записать выражения для функции плотности вероятности и функции распределения исследуемой величины. Плотность вероятности в данном случае рассчитывается по следующей формуле:

. (2.17)
Функция распределения случайной величины по нормальному закону выглядит следующим образом:

. (2.18)
Эмпирическая и теоретическая кривые распределения представлены на рисунке 2.4 и 2.5.
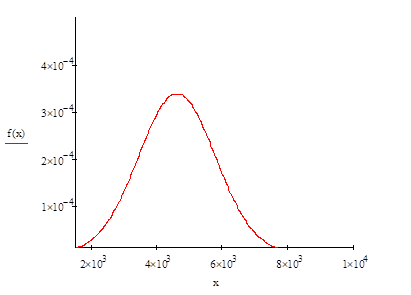
Рисунок 2.4 Теоретическая кривая распределения
Плотность вероятности рассчитывается по следующей формуле:

.
Оценка согласованности теоретического и эмпирического распределений может производиться по критерию Пирсона.
Для этого вычисляют статистику хи-квадрат по формуле

, (2.19)
Где npJ - теоретическая частота попадания случайной величины в j-й интервал; N0 - число интервалов с учетом их объединения для расчета статистики критерия Пирсона.
Для расчета критерия Пирсона интервалы рекомендуется объединять на концах таким образом, чтобы MJ ?5 или npJ ?10. Однако число N0 не должно быть менее четырех. В соответствии с этим требованием для расчета критерия Пирсона интервалы объединяются следующим образом:
Таблица 2.4 Интервалы для расчета критерия Пирсона
|
Номер интервала |
Диапозон |
Частота |
|
1 |
1569 - 2505 |
10 |
|
2 |
2505 - 3441 |
46 |
|
3 |
3441 - 4377 |
93 |
|
4 |
4377 - 5313 |
113 |
|
5 |
5313 - 6249 |
69 |
|
6 |
6249 - 7185 |
26 |
|
7 |
7185 - 9993 |
22 |
Вероятность pJ определяется по формуле:
PJ = Р(ХJ-1 < х < ХJ) = F(ХJ) - F(ХJ-1), (2.20)
Где F(х) - значение функции распределения в точке х.

PJ = - .

Расчет критерия Пирсона предстален в таблице 2.5.
Таблица 2.5 Расчет критерия Пирсона
|
Интервал |
Частоты mJ |
Частости wJ= mJ/nJ |
PJ |
NpJ |
(mJ-npJ) 2/npJ |
|
1569 - 2505 |
10 |
0,0274 |
0,0320 |
11,680 |
0,2416 |
|
2505 - 3441 |
46 |
0,1260 |
0,1230 |
44,895 |
0,0272 |
|
3441 - 4377 |
93 |
0,2548 |
0,2610 |
95,265 |
0,0539 |
|
4377 - 5313 |
113 |
0,3096 |
0,3030 |
110,595 |
0,0523 |
|
5313 - 6249 |
69 |
0,1890 |
0,1940 |
70,810 |
0,0463 |
|
6249 - 7185 |
26 |
0,0712 |
0,0680 |
24,820 |
0,0561 |
|
7185 - 9993 |
8 |
0,0219 |
0,0150 |
5,475 |
1,1645 |
|
Критерий Пирсона |
1,6419 |
Полученное значение критерия сравнивается с табличным, которое находится в зависимости от доверительной вероятности и числа степеней свободы r.
Уровень значимости г представляет собой вероятность отклонения верной гипотезы. Проверку соответствия теоретического и эмпирического распределений рекомендуется проводить при г = 0,05 - 0,1. При больших значениях г выше требования к согласованности распределений.
Число степеней свободы определяется по формуле:
R = N0 - k - 1, (2.22)
Где N0 - число интервалов после объединения для расчета статистики критерия хи-квадрат;
K - число параметров рассматриваемой теоретической функции распределения.
R = 7 - 2 - 1 = 4.
При уровне значимости 0,05 и числе степеней свободы 4 табличное значение критерия Пирсона составляет 9,4877 , а расчетный - 1,6419, то есть гипотеза о том, что распределение посуточного объема перевозок подчиняется нормальному закону, верна.
Похожие статьи
-
Автовокзал - комплекс сооружений для обслуживания пассажиров междугородных и пригородных автобусных сообщений в больших городах на конечных пунктах...
-
В данном пункте представлено описание подключенных систем к общей инфраструктуре ИС компании. В случае IBM SPSS: Вследствие того, что сбор данных с...
-
Этапы жизненного цикла БД включают: -Планирование БД - определяются принципы, задачи создания БД. -Проектирование БД. -Материализация БД -...
-
Исходные данные к курсовому проектированию Количество информационных символов k0 = 2 двоичных символа. Количество входов пороговых элементов - 2. Расчет...
-
Наиболее распространенная форма - ЭВМ. Раньше чаще использовались вычислительные центры (ВЦ). Вычислительный центр - организуется и специализируется на...
-
При работе над проектом разрабатывались два основных компонента системы: база данных (далее - БД) и интерфейс клиентского приложения. Затем необходимо...
-
Создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки...
-
Excel программирование статистический Статистические функции Применение статистических функций облегчает пользователю статистический анализ данных. Целый...
-
Операторы языка SQL - Основные понятия систем базы данных
SELECT служит для получения любого количества данных из одной или нескольких таблиц. В общем случае результатом выполнения предложения SELECT ЯВЛЯЕТСЯ...
-
Создание таблиц базы данных в Database Desktop Database Desktop - это утилита, во многом похожая на Paradox, которая поставляется вместе с Delphi для...
-
На каждом уровне управления имеются индивидуальные черты делового процесса принятия решений. Это напрямую относится к выработке решений в управленческих...
-
Типы полей ограничивают вводимую пользователем информацию по содержанию. В Системе используются следующие типы полей данных: Text . Поле ввода текста в...
-
Выбор системы управления базами данных является одним из важных этапов при разработке автоматизированной системы расписания занятий. Выбранный...
-
Системы автоматизированного проектирования - Теоретические основы информационных технологий
Близкими по своей структуре и функциям к системам автоматизации научных исследований оказываются системы автоматизированного проектирования (САПР). САПР...
-
Цель создания САПР - Состав систем автоматизированного проектирования
Под автоматизацией проектирования понимают систематическое применение ЭВМ в процессе проектирования при научно обоснованном распределении функций между...
-
Формирование выборки случайных чисел, распределенных по заданному закону распределения
Лабораторная работа Тема: Формирование выборки случайных чисел, распределенных по заданному закону распределения Цель: освоение методов генерации...
-
ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ База данных как основа информационного обеспечения В состав информационного, программного и математического обеспечения...
-
Базы данных - это определенная совокупность информационных данных, отображающих в максимально возможной полноте состояние тех или иных объектов или...
-
Методы и средства проектирования - Автоматизированные системы обработки экономической информации
Проектирование - процесс создания проекта-прототипа, прообраза предполагаемого или возможного объекта, его состояния. Современная технология создания АИС...
-
Распечатки экранов ПК Рис.5. Форма "Главное меню" Рис.6. Форма "Специальности" Рис.7. Форма "Личные карточки" Рис.8. Форма "Поощрения" Рис.9. Форма...
-
Наиболее распространенная форма - ЭВМ. Раньше чаще использовались вычислительные центры (ВЦ). Вычислительный центр - организуется и специализируется на...
-
Таблица 2. Структура записей таблицы "Специальности" № п/п Имя поля в таблице Тип данных Размер поля Ключевое поле 1 № специальности Числовой (INT)...
-
База данных представляет собой информационную модель того объекта (организации или предприятия), информация о котором требуется пользователю для...
-
Над созданием ИС "Учет посещаемости в детском саду" будет работать определенная группа разработчиков, состоящая из руководителя и инженера-программиста....
-
Способы обработки данных - Автоматизированные системы обработки экономической информации
Различаются следующие способы обработки данных: централизованная, децентрализованная, распределенная и интегрированная. Централизованная предполагает...
-
Основным компонентом АРМ является база данных (БД). Использование БД является эффективным средством разработки и поддержки информационного обеспечения...
-
Средства обработки данных - Автоматизированные системы обработки экономической информации
Это компьютеры - 4 класса: микро, малые (мини); большие и суперЭВМ. Главные хар-ки ЭВМ - быстродействие и объем памяти. МикроЭВМ - 2 группы: 1....
-
Рабочее место -- это зона нахождения работника и средств приложения его труда, которая определяется на основе технических и эргономических нормативов и...
-
Логическая модель данных Логическая модель данных представлена сущностями (таблицами). Таблицы - фундаментальные объекты реляционной базы данных, в...
-
Типы данных и команды SQL - Разработка информационной системы "Магазин компьютерных товаров"
Microsoft SQL Server поддерживает большинство типов данных SQL 2003. Также SQL Server поддерживает дополнительные типы данных, используемые для...
-
Структура SQL - Банки и базы данных. Системы управления базами данных
Широкое развитие информационных систем и связанная с этим унифицированность информационного пространства привело к необходимости создания стандартного...
-
В настоящее время существует несколько видов СУБД. Для создания базы данных "Учет посещаемости в детском саду" была выбрана СУБД Paradox. Выбор...
-
Модель сущность-связь представлена в приложении 1. Структура таблиц Следует отметить назначение полей, которые встречаются во всех таблицах: - id --...
-
Нет необходимости для детального рассмотрения предлагающихся разнообразных направлений классификации информации. Выделим только те признаки информации,...
-
Значительное влияние на процесс дифференциации и интеграции управленческого труда оказывает возрастание сложности и масштабов решаемых управленческих...
-
Объектно-ориентированные СУБД Несмотря на большую популярность реляционных СУБД, развитие технологии появления данными на них не остановилось. Развитие...
-
Физическая модель базы данных определяет способ размещения данных в среде хранения и способ доступа к этим данным, которые поддерживаются на физическом...
-
В деятельности крупных фирм (в особенности транснациональных корпораций, представляющих собой комплексы большого числа взаимосвязанных и...
-
Для того чтобы оценить экономическую выгоду от внедрения АИС необходимо вычислить трудозатраты компании направленные непосредственно на реализацию...
-
Функции CAD-систем в машиностроении подразделяют на функции двухмерного (2 D ) и трехмерного (3 D ) проектирования. К функциям 2 D Относятся черчение,...
Статистическая обработка исходных данных - Проектирование автоматизированной системы резервирования мест и продажи билетов на автовокзале