Классификация систем счисления - Компьютерная арифметика
В настоящее время различают Позиционные И Непозиционные системы счисления. Классификация систем счисления приведена на рис. 2.1.
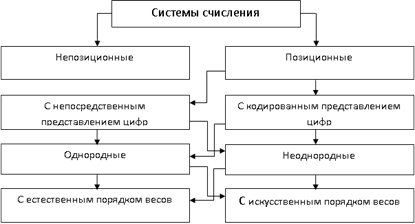
Рисунок 2.1 -- Классификация систем счисления
Непозиционная Система счисления: это такая система счисления, в которой каждой цифре на любом ее месте в записи числа однозначно соответствует один и тот же количественный эквивалент.
Наиболее известным примером такой системы является Римская система счисления, рис. 2.2, например:
|
Десятичные числа: |
1 |
5 |
10 |
50 |
100 |
500 |
1000 |
|
Римские цифры: |
I |
V |
X |
L |
C |
D |
M |
Рисунок 2.2 - Соответствие десятичных чисел римским цифрам
В римской системе счисления несколько стоящих рядом одинаковых цифр суммируются рис.2.3:
XXX = X+X+X= 30(10).
Рисунок 2.3 - Пример записи числа с основанием (10) в Римской системе счисления
Если рядом стоят разные цифры, причем младшая - справа от старшей, то они также суммируются, рис.2.4:
XVI = X+V+I = 16(10).
Рисунок 2.4 - Пример записи числа с основанием (10) в Римской системе счисления
Если же младшая цифра находится слева от старшей, то она вычитается из этой старшей цифры рис.2.5:
IX = X - I = 9(10).
Рисунок 2.5 - Пример записи числа с основанием(10) в Римской системе счисления
Недостатки римской системы счисления заключаются в следующем:
- - в пределе, теоретически, она имеет бесконечное количество цифр; - арифметические действия над числами очень сложны; - отсутствует цифра {0}.
Позиционная Система счисления: это такая система счисления, в которой одной и той же цифре в зависимости от ее местоположения в записи числа соответствуют различные количественные эквиваленты. Наиболее известным примером такой системы является Десятичная система счисления, например: цифры 1 и 2 в зависимости от местоположения этих цифр в числе изменяется значение самого числа рис.2.6:
|
Разряды: |
Десятки |
Единицы |
|
Цифры: |
1 |
2 |
Рисунок 2.6 - Пример записи числа в десятичной системе счисления
При таком положении цифр получается число Двенадцать (12(10)). Нижний индекс при записи числа обозначает основание системы счисления, в данном случае ((10)) означает десятичную систему счисления. Если поменять местами цифры 1 и 2, рис.2.7:
|
Разряды: |
Десятки |
Единицы |
|
Цифры: |
2 |
1 |
Рисунок 2.7 - Пример записи числа в десятичной системе счисления
Получается число Двадцать один (21(10)). Для определения количественного эквивалента полной записи числа в позиционной системе счисления используется некоторая функция от количественных эквивалентов цифр. Если этой функцией является функция сложения, то систему называют Аддитивной, если же используется функция умножения - систему называют Мультипликативной.
Любое число в позиционной системе счисления может быть записано в виде:

(2.4)

Где - количественный эквивалент числа (А), состоящего из (n) цифр;
- - цифра, ; - основание системы счисления.
В левой части равенства записано символическое изображение числа.
В правой части равенства показано, что все цифры числа в разных позициях имеют разный вес, при этом каждая позиция с присвоенными ей номером и весом называется - разрядом числа.
Правило: Количественный эквивалент числа в позиционной системе счисления равен сумме произведений количественных значений цифр и степеней основания, показатели которых равны номерам разрядов, причем нумерация разрядов начинается с (0).

Например: , n=4, p=10, тогда можно записать:

(2.5)
Тогда:

.
Однородность системы счисления означает, что во всех разрядах числа, записанного в такой системе, используют цифры из одного и того же множества.
Например, в обычной десятичной системе счисления во всех разрядах числа используются цифры из множества рис.2.8:
{0,1,2,3,4,5,6,7,8,9},
Рисунок 2.8 - Множество цифр использующихся в десятичной системе счисления
В двоичной системе счисления используются цифры из множества рис.2.9:
{0,1},
Рисунок 2.9 - Множество цифр использующихся в двоичной системе счисления
В троичной системе счисления используются цифры из множества рис.2.10:
{0,1,2},
Рисунок 2.10 - Множество цифр использующихся в троичной системе счисления
В пятеричной системе счисления используются цифры из множества рис.2.11:
{0,1,2,3,4},
Рисунок 2.11 - Множество цифр использующихся в пятеричной системе счисления
В восьмеричной системе счисления используются цифры из множества рис.2.12:
{0,1,2,3,4,5,6,7},
Рисунок 2.12 - Множество цифр использующихся в восьмеричной системе счисления
В шестнадцатеричной системе счисления при записи числа используются цифры и буквы рис.2.13:
{0,1,2,3,4,5,6,7,8,9,A, B, C, D, E, F}.
Рисунок 2.13 - Множество цифр и букв использующихся в шестнадцатеричной системе счисления
Если позиционная система счисления Однородная с непосредственным представлением цифр и с естественным порядком весов, то любое число может быть представлено в виде суммы попарных произведений:

(2.6)
Где - количественный эквивалент числа (А);
- - цифра, - основание системы счисления. S - количество разрядов в целой части числа слева от запятой;
M - количество разрядов в дробной части числа справа от запятой.
Исходя из выше сказанного можно записать:

.
Или:

.
Соответствие чисел в (10 - ой), (16 - ой), (8 - ой) и (2 - ой) системах счисления приведены в табл. 2.1.
Таблица 2.1 - Соответствие чисел в (10 - ой), (16 - ой), (8 - ой) и (2 - ой) системах счисления
|
Десятеричная Х(10) |
Шестнадцатеричная Х(16) |
Восьмеричная Х(8) |
Двоичная Х(2) |
|
0 |
0 |
0 |
0000 |
|
1 |
1 |
1 |
0001 |
|
2 |
2 |
2 |
0010 |
|
3 |
3 |
3 |
0011 |
|
4 |
4 |
4 |
0100 |
|
5 |
5 |
5 |
0101 |
|
6 |
6 |
6 |
0110 |
|
7 |
7 |
7 |
0111 |
|
8 |
8 |
10 |
1000 |
|
9 |
9 |
11 |
1001 |
|
10 |
А |
12 |
1010 |
|
11 |
В |
13 |
1011 |
|
12 |
С |
14 |
1100 |
|
13 |
D |
15 |
1101 |
|
14 |
Е |
16 |
1110 |
|
15 |
F |
17 |
1111 |
Помимо Позиционных однородных систем известны также Позиционные неоднородные (смешанные) системы счисления.
В таких системах цифры в разных разрядах могут принимать значения из различных множеств.
Задают неоднородные системы с помощью двухстрочных матриц вида:

(2.7)
Здесь в первой строке матрицы указано число разрядов (tI), отводимых в (i-й) группе разрядов (i=) представления числа для записи цифр по основанию (kI), которое указано во второй строке того же столбца.
Неоднородные системы Счисления, так же как и однородные, могут быть с Непосредственным и с Кодированным представлением цифр.
Примером смешанной системы с кодированным представлением цифр Является система измерения времени (в годах, месяцах, неделях, сутках, часах, минутах и секундах).
Например: надо выразить время в 2- года, 25 - суток, 14 - часов, 35 - минут и 48 секунд, в секундах. Тогда можно записать, что основание в каждом разряде равно:

Цифры имеют следующие значения:

По формуле (2.4) можно записать:
.
Существует так же неоднородная двоично-пятиричная система счисления, в которой в нечетных разрядах основание р1=5,(аІ= 0 - 4), а в четных разрядах основание р2=2,(аІ= 0,1).
Так как произведение весов двух соседних (четного и нечетного) разрядов равно десяти, то двумя двоично-пятиричными разрядами можно кодировать одну десятичную цифру.
Пример записи десятичных цифр от 0 до 9 в двоично-пятиричной системе приведен в табл. 2.2.
Таблица 2.2 - Пример записи десятичных цифр в двоично-пятиричной системе
|
А(10) |
А(2-5) |
А(10) |
А(2-5) |
|
0 |
00 |
5 |
10 |
|
1 |
01 |
6 |
11 |
|
2 |
02 |
7 |
12 |
|
3 |
03 |
8 |
13 |
|
4 |
04 |
9 |
14 |
Например: записать число 853(10) в двоично-пятиричной системе счисления.
Решение: исходя из значений, представленных в табл. 2.2 имеем:
|
8(10)=13(2-5) |
|
5(10)=10(2-5) |
|
3(10)=03(2-5) |
Тогда: А(10) = 131003(2-5).
Существует так же Кодированные системы счисления - это позиционные системы счисления, в которых цифры одной системы счисления кодируются при помощи цифр другой системы, а число в общем виде записывается следующим образом:

. (2.8)
Где: А - число;
- - цифра; - основание системы счисления, символами которой кодируются цифры;
Р - основание исходной системы счисления.
Классическим примером кодированной системы счисления есть - двоично-десятичная система.
При двоично-десятичном кодировании каждая десятичная цифра заменяется тетрадой (четверкой) двоичных цифр, а сами тетрады записываются последовательно в соответствии с порядком следования десятичных цифр.
При обратном преобразовании двоично-десятичного кода в десятичный исходный код разбивается на тетрады вправо и влево от запятой, которые затем заменяются десятичными цифрами.
Таким образом, при двоично-десятичном кодировании фактически не производится перевод числа в новую систему счисления, а мы имеем деле с двоично-кодированной десятичной системой счисления.
Например: десятичное число 12(10) записать в двоично-десятичной системе счисления = 00010010(2-10).
При построении кодированных позиционных систем счисления в качестве весов разрядов могут быть выбраны как члены геометрической прогрессии, так и произвольные числа.
В зависимости от этого кодированные системы счисления делятся на кодированные системы счисления с естественными разрядами весов и на кодированные системы счисления с искусственными разрядами весов.
Кодированные системы счисления с естественными разрядами весов - это позиционная система счисления, в которой в качестве весов разрядов используются члены геометрической прогрессии.
Примером системы счисления с естественными разрядами весов может служить двоично-десятичная система с весами (8-4-2-1).
Кодированные системы счисления с искусственными разрядами весов - это позиционная система счисления, в которой в качестве весов разрядов используются произвольные числа.
Примером системы счисления с искусственными разрядами весов может служить двоично-десятичная система с весами (2-4-2-1, 5-2-1-3).
Искусственный порядок весов широко применяется в аналогово-цифровых и цифро-аналоговых преобразователях.
В табл. 2.3 представлены числа, записанные в десятичной системе счисления и в кодированной системе счисления с естественным и искусственным порядком весов.
Таблица 2.3 - Числа десятичной системы счисления и кодированной системе счисления с естественным и искусственным порядком весов.
|
Десятичная СС |
Кодированная СС 8-4-2-1 |
Кодированная СС 4-2-2-1 |
Кодированная СС 2-4-2-1 |
|
0 |
0000 |
0000 |
0000 |
|
1 |
0001 |
0001 |
0001 |
|
2 |
0010 |
0010 |
0010 |
|
3 |
0011 |
0011 |
0011 |
|
4 |
0100 |
0110 |
0100 |
|
5 |
0101 |
0111 |
0101 |
|
6 |
0110 |
1010 |
0110 |
|
7 |
0111 |
1011 |
0111 |
|
8 |
1000 |
1110 |
1110 |
|
9 |
1001 |
1111 |
1111 |
Например: десятичное число 1593(10) в двоично-десятичной системе счисления с естественными разрядами весов 8-4-2-1 имеет вид: 0001 0101 1001 0011, а в двоично-десятичной системе счисления с искусственными разрядами весов 2-4-2-1 имеет вид: 0001 0101 1111 0011.
В современных компьютерных системах помимо рассмотренных систем счисления встречаются и системы счисления с непостоянными разрядами весов. Наиболее известным примером таких систем является код Грея.
Кодом Грея порядка (n) называется любая циклическая последовательность всех наборов из (0) и (1) длины (n), в которой два соседних набора отличаются ровно в одной компоненте.
Код Грея является одношаговым кодом, т. е. при переходе от одного числа к другому всегда меняется лишь какой то один из всех битов. Соответствие десятичных чисел в диапазоне от 0 до 15 двоичным числам и коду Грея приведено в табл. 2.4.
В двоичном коде при переходе от изображения одного числа к изображению соседнего числа может происходить одновременное изменение цифр в нескольких разрядах, что может явиться источником ошибок, в работе аппаратуры в некоторых случаях например при переходе от 7 к 8.
В коде Грея два соседних значения отличаются только в одном разряде.
Двоичные разряды в коде Грея не имеют постоянного веса. Код Грея изначально предназначался для защиты от ложного срабатывания электрических переключателей. Сегодня код Грея широко используется для упрощения выявлений и исправления ошибок в системах связи.
Таблица 2.4 - Соответствие десятичных чисел в диапазоне от 0 до 15 двоичным числам и коду Грея
|
Десятичные числа |
Двоичные числа |
Код Грея |
|
0 |
0000 |
0000 |
|
1 |
0001 |
0001 |
|
2 |
0010 |
0011 |
|
3 |
0011 |
0010 |
|
4 |
0100 |
0110 |
|
5 |
0101 |
0111 |
|
6 |
0110 |
0101 |
|
7 |
0111 |
0100 |
|
8 |
1000 |
1100 |
|
9 |
1001 |
1101 |
|
10 |
1010 |
1111 |
|
11 |
1011 |
1110 |
|
12 |
1100 |
1010 |
|
13 |
1101 |
1011 |
|
14 |
1110 |
1001 |
|
15 |
1111 |
1000 |
Похожие статьи
-
Системы счисления. Представление данных в ЭВМ - Основы программирования
В современном мире для записи числовой информации используют позиционные системы счисления, в которых числа записываются с помощью ограниченного...
-
Системы счисления - Компьютерная арифметика
Как было отмечено в первой главе Система счисления - совокупность приемов и правил для установления однозначного соответствия между любым числом и его...
-
Системы счисления - Основы информатики
1.1 Переведите число 154,23510 из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную системы счисления Решение: При переводе из...
-
Базовые понятия и определения компьютерной арифметики - Компьютерная арифметика
Компьютерная арифметика - совокупность принципов и форм представления числовой информации, методов и алгоритмов выполнения арифметических операций и...
-
10 2 4 8 16 0 0 0 0 0 1 1 1 1 1 2 10 2 2 2 3 11 3 3 3 4 100 10 4 4 5 101 11 5 5 6 110 12 6 6 7 111 13 7 7 8 1000 20 10 8 9 1001 21 11 9 10 1010 22 12 A...
-
Классификация эк. информации (И) - Автоматизированные системы обработки экономической информации
Классификация - упорядочение некоторого множества объектов в соответствии с установленными признаками их сходства и различия. Признак сходства или...
-
Классификация по типу интерактивности Для того, чтобы правильно понять, оценить, грамотно разработать и использовать информационные технологии в...
-
В повседневной жизни мы постоянно сталкиваемся с экспертами в самых различных областях человеческой деятельности - врачи, преподаватели, референты и т....
-
Классификация экспертных систем, Медицинская диагностика., Прогнозирование. - Экспертные системы
Медицинская диагностика. - Диагностические системы используются для установления связи между нарушениями деятельности организма и их возможными...
-
Человек получает представление об окружающем пространстве с помощью большого набора органов чувств. Система дополненной реальности, являясь посредником...
-
Анализ основных вопросов классификаций распределительных вычислительных систем
Сегодня к распределенным вычислительным системам относят: вычислительные кластеры, SMP - симметричные мультипроцессоры, DSM - системы с распределенной...
-
Классификация корпоративных информационных систем - Корпоративные информационные системы
Корпоративные информационные системы можно разделить на два класса: финансово-управленческие и производственные. 1. Финансово-управленческие системы...
-
Классификация АИС по функциональному признаку Функциональный признак определяет назначение подсистемы, а также ее основные цели, задачи и функции....
-
Классификация массивов - История создания и развития автоматизированных информационных систем
Организационная подборка сведений о каком-либо объекте или процессе либо о ряде однородных объектов или процессов называется массивом информации. 1. По...
-
Классификация компьютерных сетей - Теоретические основы информационных процессов и систем
Для классификации компьютерных сетей используются разные признаки, выбор которых заключается в том, чтобы выделить из существующего многообразия такие,...
-
Угроза - целенаправленное действие, которое повышает уязвимость накапливаемой, хранимой и обрабатываемой системы информации и приводит к ее случайному...
-
- Статические ЭС разрабатываются в предметных областях, в которых база знаний и интерпретируемые данные не меняются во времени. Они стабильны. Пример:...
-
Без использования измерительных приборов невозможно представить многие грани человеческой деятельности:начиная от научной работы и заканчивая...
-
Классификация по степени автоматизации - Исследование информационной системы
По степени автоматизации ИС делятся на: Автоматизированные: информационные системы, в которых автоматизация может быть неполной (то есть требуется...
-
Классификации СППР - Система поддержки принятия решений
Для СППР отсутствует не только единое общепринятое определение, но и исчерпывающая классификация. Разные авторы предлагают разные классификации. На...
-
Хотя существует множество инновационных способов использования дополненной реальности, можно выделить четыре типа приложений, в которых чаще всего...
-
В современной технологии баз данных предполагается, что создание базы данных, ее поддержка и обеспечение доступа пользователей к ней осуществляются...
-
Классификация и анализ источников угроз и уязвимостей безопасности В информационной безопасности под угрозой понимают потенциальное событие или действие,...
-
Понятие информационных технологий - Классификация и развитие информационных систем и технологий
Информационная технология -- это процесс, использующий совокупность средств и методов сбора, обработки и передачи данных для получения информации нового...
-
Из всех изделий микроэлектроники наибольшее распространение получили интегральные микросхемы. Именно они характеризуют современный уровень развития...
-
Классификация систем электронного документооборота International Data Corporation (далее IDC) является аналитической фирмой, которая специализируется на...
-
Классификация имитационных моделей - Имитационные модели информационных систем
Имитационные модели принято классифицировать по четырем наиболее распространенным признакам: Типу используемой ЭВМ; Способу взаимодействия с...
-
Области применения экспертных систем - Экспертные системы
Области применения систем, основанных на знаниях, могут быть сгруппированы в несколько основных классов: медицинская диагностика, контроль и управление,...
-
Техническое обеспечение (ТО) - совокупность технических средств, предназначенных для работы информационной системы, а также соответствующая документация...
-
Координатная система. Картографическая проекция и ее классификация - Геоинформационные системы
Система координат определяет единицы измерения, которые используются для определения положения объекта на двумерной поверхности, и начало координат для...
-
Архивация информации - это такое преобразование информации, при котором объем файла уменьшается, а количество информации остается прежним. Архивный файл...
-
Операционная система - совокупность программных средств, обеспечивающая управление аппаратной частью компьютера и прикладными программами, а также их...
-
Классификация ИС. Жизненный цикл ИС и его модели - Теория экономических информационных систем
Классификация по масштабу По масштабу информационные системы подразделяются на следующие группы 1. одиночные;2. групповые;3. корпоративные. Одиночные...
-
Файловая система - это часть операционной системы, назначение которой состоит в том, чтобы обеспечить пользователю удобный интерфейс при работе с...
-
Компьютерные информационные технологии в управлении экономическим объектом. Классификация систем управления Богатейший бизнесмен планеты Бил Гейтс,...
-
Дисковые разделы, MBR, загрузочные сектора и таблица разделов - Операционная система Linux
Весь жесткий диск может быть разбит на несколько разделов, причем каждый раздел представлен так, как если бы это был отдельный диск. Разделение...
-
Понятие электронного бизнеса в Интернет Глобальная сеть Интернет представляет собой особую индустрию, средство транспортировки информации до...
-
Структура SQL - Банки и базы данных. Системы управления базами данных
Широкое развитие информационных систем и связанная с этим унифицированность информационного пространства привело к необходимости создания стандартного...
-
Рассмотрим замкнутую сеть массового обслуживания с разнотипными заявками, которая является вероятностной моделью обслуживания заявок в УП "Проектный...
-
Описание динамики системы программируемости данного вида деятельности составляет основу любой автоматизированной информационной системы специального...
Классификация систем счисления - Компьютерная арифметика