Применение математики в конструировании одежды
Особенную важность имеют те методы науки, которые позволяют решать задачу, важную для всей практической деятельности человека: как распорядиться своими средствами для достижения по возможности больших результатов. С такими задачами приходится иметь дело представителям самых разных профессий - конструкторы стремятся найти оптимальный и безопасный режим работы атомного реактора, военные ломают голову, стремясь сделать "невидимым" для противника подводный крейсер, экономисты стараются так организовать управление и планирование, чтобы предприятие работало наиболее эффективно и т. д.
Решение таких задач невозможно без применения математики и методов математического и компьютерного моделирования.
Математическая модель - это записанная в математических символах абстракция реального явления, причем так конструируемая, чтобы ее анализ давал возможность проникнуть в сущность явления. Для принятия определенных решений на основе исследования математической модели необходимо владение математическим аппаратом для решения возникающих задач, разработки компьютерных алгоритмов, позволяющих находить решение задачи с помощью ЭВМ.
Следует особенно подчеркнуть роль математики в процессе моделирования. Нередко красивая математическая теория, которая сейчас кажется далекой от практики, используется для самых неожиданных приложений. Развитие и расширение возможностей компьютеров дает основу для анализа более сложных моделей, описывающих процессы в экономике, технике и естествознании и требует, соответственно, новых математических методов.
Пропорции -- Размерные соотношения элементов формы. Пропорциональные соотношения -- это соразмерность элементов, единство частей и целого. В моделировании одежды пропорции являются самым главным фактором. Пропорции делятся на две группы: Простые (основанные на рациональных числах) и Сложные (основанные на иррациональных числах, производных геометрических построений). Простые пропорциональные отношения выражаются дробным числом, где числитель и знаменатель -- это целые числа от 1 до 8. Например, рукав 3/4, юбка-мини 1/3, пальто 7/8, свитер 2/3 от целого. На рис. 1 приведены примеры встречающихся в моделировании пропорциональных соотношений. К простым пропорциональным отношениям относится так называемый "египетский треугольник" с соотношением сторон: 3:4:5 (рис. 1, А).
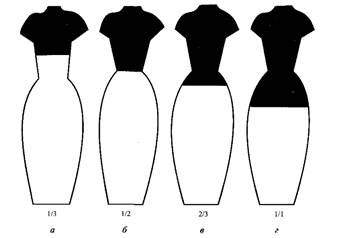
Рис. 1. Примеры часто встречающихся в моделировании пропорциональных отношений: а -- завышенная линия лифа (лиф -- I часть, нижняя часть платья -- 3 части); б -- линия лифа расположена на линии талии (лиф -- 1 часть, юбка -- 2 части); в -- линия лифа чуть занижена (лиф -- 2 части, юбка --,3 части), такие пропорции приближаются к "золотому сечению"; г -- лиф и юбка по длине одинаковы (лиф -- 1 часть, юбка -- 1 часть).
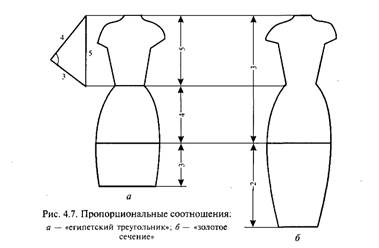
Начиная с древности, велись поиски наиболее гармоничных пропорций, которые можно было использовать в архитектуре, строительстве, инженерных сооружениях. Найденные сложные пропорции основаны на иррациональных числах, которые выводились геометрическими построениями:
"Треугольник Пифагора" -- прямоугольный треугольник с углами в 30, 60 и 90 градусов и гармоничным соотношением сторон;
"Золотое сечение", получаемое при делении целого на две неравные части, где целое так относится к большей части, как большая часть --- к меньшей. В некотором приближении отношения "золотого сечения" можно представить в виде ряда: 2/3, 3/5, 5/8, 8/13 (рис. 4.7, Б);
Хочется затронуть тему "золотого сечения", так как в процессе конструирования одежды мы имеем дело с цифрами, расчетами и отношениями. Уж если в архитектуре с античных времен используют это соотношение, то почему бы нам не разобраться, и не внедрить в нашу работу.
Красота скульптуры, красота храма, красота картины, симфонии, поэмы... Что между ними общего? Разве можно сравнивать красоту храма с красотой ноктюрна? Оказывается можно, если будут найдены единые критерии прекрасного, если будут открыты общие формулы красоты, объединяющие понятие прекрасного самых различных объектов - от цветка ромашки (разве он не прекрасен?!) до красоты обнаженного человеческого тела.
Из многих отношений, которыми издавна пользовался человек при создании гармонических произведений, существует одно, единственное и неповторимое, обладающее уникальными свойствами. Оно отвечает такому делению целого на две части, при котором отношение большей части к меньшей равно отношению целого к большей части. Эту пропорцию называли по-разному - "золотой", "божественной".
Древнейшие сведения о ней относятся ко времени расцвета античной культуры. О золотой пропорции упоминается в трудах великих философов Греции Пифагора, Платона, Евклида.
Художник и инженер Леонардо да Винчи, изучавший и восхвалявший золотую пропорцию на протяжении всей своей жизни, называет ее "золотое сечение". Название Леонардо да Винчи сохранилось и сегодня.
Рассмотрение особенностей проявления золотой пропорции - от объектов природы до произведений искусств и составляет предмет нашего проекта.
Деление целого на две части, при котором отношение большей части к меньшей равно отношению целого к большей. Схематично это выглядит так:
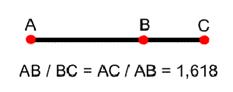
В процентах выходит так:
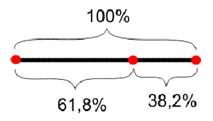
Посмотрим, как это выглядит на практике.



Впечатляет? Подобных примеров в искусстве, природе и древней архитектуре бесконечное множество. Увлекательное скажу вам занятие. Для нас, как создателей одежды, самым важным будет разобрать пропорции фигуры человека.
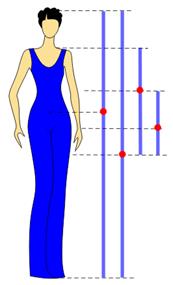
Трудно оторвать глаза от красоты, она так притягательна, может причина в нем - золотом и божественном. Надо заметить, человек способен интуитивно чувствовать пропорции сечения. Работая над картиной, вышивкой или костюмом, сам того не зная, закладывает Его в свои творения. Ничего удивительного, ведь золотая пропорция у нас всегда перед глазами, в виде самих себя. Тогда вперед за работу, но теперь уже не пальцем в небо, а точно и наверняка.
Коэф_зол_сеч1 = 1.618;
Коэф_зол_сеч2 = 0.618;
Коэф_зол_сеч3 = 0.382;

Пропорция человеческого тела
Золотое сечение является основой построения гармоничных форм, так как является абсолютным законом формообразования в природе, частью которой мы являемся.
Законы гармонии - есть числовые законы. Поэтому необходимо использовать знания и опыт человечества для развития подходов при определении форм моделей в ваших виртуальных мирах.
Моделируя обычного человека, мы, скорее всего, не берем линейку и калькулятор, высчитывать золотые пропорции. Мы просто интуитивно ощущаем эти формы, ибо формы человеческого существа попадаются нам на глаза чаще, чем что-либо другое, но создавая модель необычного существа, растения, сооружения, нам стоит использовать знания геометрии и золотого сечения, чтобы на результат работы можно было смотреть без отвращения, хотя... если вы добиваетесь как раз чувства отвращения, то вы знаете, что вы должны делать.
В любом случае, знание законов природы (числовых законов), помогает нам как можно быстрее достичь желаемого результата.
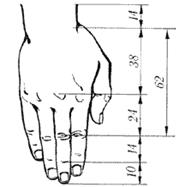
Немецкий профессор Цейзинг в середине 18 столетия проделал огромную работу: он измерил более 2000 тел и высказал предположение, что золотое сечение выражает среднестатистический закон: деление тела точкой пупа - один из основных показателей золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13: 8 = 1,625. Пропорции золотого сечения проявляются и в отношении других частей тела - длина плеча, предплечья и кисти, кисти и пальцев и т. д.
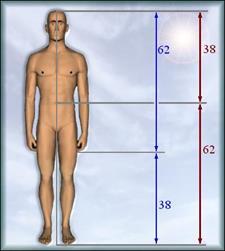
У маленьких детей (около года) пропорция составляет отношение 1: 1.
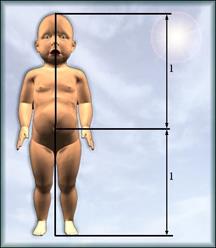
Голова человека тоже проявляет пропорции золотого сечения:
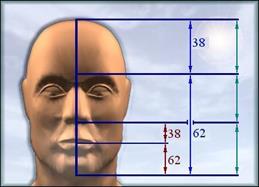
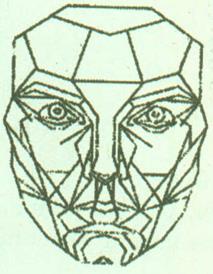
Недавно наш современник, американский хирург Стивен Маркварт создал, используя принцип "золотого сечения", геометрическую маску, которая может служить эталоном прекрасного лица. Чтобы узнать, соответствует ли лицо идеалу, достаточно скопировать маску на прозрачную пленку и наложить ее на фотографию соответствующего размера.
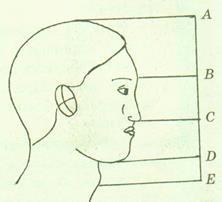
Так, разделив в отношении" золотого сечения" отрезок, заключенный между макушкой и адамовым яблоком, мы получим точку, лежащую на линии бровей (В). При дальнейшем золотом делении образовавшихся частей получим последовательно кончик носа (С), конец подбородка(Д).
"квадраты Фибоначчи" с резким убыванием отношения стороны к диагонали (рис. 4.8, и);
"динамические прямоугольники" и прямоугольники с отношением сторон, которые дают иллюзию постепенного едва заметного убывания (рис. 2, Б).
Таким образом, из сказанного выше напрашивается вывод, что гармоничные пропорциональные отношения основаны на неравенстве пропорций. В моделировании одежды пропорциональные отношения определяются интуитивно или задаются тенденциями моды. Каждое модное направление предлагает свои пропорциональные членения костюма и, тем самым, человека в костюме.
Похожие статьи
-
Цели метода конструирование, в конечном счете, следующие: - получение более лучших и более экономичных изделий; - рационализация и создание предпосылки...
-
Сферы применения титана и титановых сплавов - Титан и титановые сплавы
Авиационная промышленность - основной потребитель титановой продукции. Именно развитие авиационной техники дало толчок титановому производству. По своим...
-
Применение лазерного луча в промышленности и технике - Лазеры
Оптические квантовые генераторы и их излучение нашли применение во многих отраслях промышленности. Так, например, в индустрии наблюдается применение...
-
Сварка электронно-лучевая и лазерная - Виды сварки и способы их применения
В промышленности все более широкое применение находят тугоплавкие и химически активные металлы и сплавы. Поэтому для их сварки необходимо применять...
-
Результирующая вольт-амперная характеристика туннельного диода определяется комбинацией туннельных и тепловых свойств и имеет довольно необычный вид. В...
-
Конструктивные схемы крепления валов перемешивающих устройств В большинстве аппаратов химической технологии с целью интенсификации проводимых процессов...
-
Введение - Применение ионного микроскопа
Ионный микроскоп - микроскоп, в котором для получения изображения применяется создаваемый источником пучок ионов. По принципу действия ионный микроскоп...
-
Получение, Применение - Целюллоза и ее применение
Образцом почти чистой целлюлозой является вата, полученная из очищенного хлопка. Основную массу целлюлозы выделяют из древесины, в которой она содержится...
-
Пластмассовые антифрикционные материалы - Пластмассы. Их свойства и области применения
Из-за малого сходства с металлами и из-за больших упругих деформаций пластмассы в узлах трения менее чувствительны к схватыванию и задиранию, что резко...
-
Пластмассы. Основные характеристики пластмасс - Пластмассы. Их свойства и области применения
Пластические массы (пластмассы, пластики) -- материалы на основе природных или синтетических полимеров, способные под влиянием нагревания и давления...
-
Анализ конструкции (объекта дипломного проектирования) на предмет снижения ее массы, применения новых материалов, совершенствования конструктивных...
-
Технологические особенности получения и применения пластмасс
1. Общие сведения о пластмассе Пластмассами называют обширную группу органических материалов, основу которых составляют искусственные или природные...
-
Диод Шоттки (назван в честь немецкого физика Baльтера Шоттки) - полупроводниковый диод с малым падением напряжения при прямом включении. Диоды Шоттки...
-
ПРИНЦИПЫ КОНСТРУИРОВАНИЯ САМОДЕЛЬНЫХ СВАРОЧНЫХ АППАРАТОВ - Самодельные сварочные аппараты
В зависимости от используемого для сварки типа тока, различают сварочные аппараты постоянного и переменного тока. Сварочные аппараты с использованием...
-
Пластмассовые уплотнители и амортизаторы. - Пластмассы. Их свойства и области применения
Детали уплотнений из пластмасс находят очень широкое применение. Это объясняется тем, что пластмассы обеспечивают не только высокую герметичность...
-
Истинная плотность полуводного гипса 2,65-2,75 г/см3. По срокам схватывания гипс делят на 3 группы (А, Б, В) Вид гипса Начало схватывания Конец...
-
Разработка теоретической схемы базирования Базирование - определение положения деталей сборочной единицы, относительно друг друга, либо сборочной единицы...
-
Выводы - Проектирование и применение токарного станка модели 1К660Ф3
Дипломный проект состоит из шести частей: - конструкторской; - технологической; - специальной; - организационно-экономической; - охраны труда и техники...
-
Расчет ведомого вала - Конструирование узлов и деталей машин
Производим расчет для опасного сечения (рис.11) (канавка для выхода шлифовального круга): Где - коэффициент запаса прочности по нормальным напряжениям; -...
-
Технологические свойства, Список используемой литературы - Область применения цементуемых сталей
Температура ковки, 0 С: начала 1250, конца 780 - 760. Охлаждение заготовок сечением до 100 мм производится на воздухе, сечения 101 - 300 мм - в мульде....
-
Расчет валов на выносливость, Расчет ведущего вала - Конструирование узлов и деталей машин
Расчет ведущего вала Производим расчет для опасного сечения (рис.10) (канавка для выхода шлифовального круга): Где - коэффициент запаса прочности по...
-
Определение формы и габаритных размеров упаковки Для разработки развертки и штанцевальной формы картонной упаковки для пищевой отрасли была выбрана...
-
Станина Станина состоит из головной части и секций, стыкуемых по длине. На головной части станины установлена передняя бабка. Остальные секции станины...
-
Основным технологическим средством автоматизации проектирования в машиностроении является цифровая ЭВМ, оперирующая с информацией, представленной в...
-
Контроль качества -- это деятельность, включающая проведение измерений, экспертизы, испытаний или оценки параметров объекта и сравнение полученных...
-
Анализ проблемы - Выбор варианта автоматизации процесса конструирования
Рассматривая появление новых технических изделий на рынке, пусть это будет сравнительно простой технический предмет потребления или сложная...
-
Ионно-лучевая литография - Применение ионного микроскопа
Традиционно, рельеф фоторезистов формируется методами сфокусированного ионного пучка и электронно-лучевой литографии. Преимущества ионно-лучевой...
-
Взаимодействие ионов с веществом - Применение ионного микроскопа
Ионы, как и электроны в СЭМ, могут проникать во внутренний объем твердых и жидких образцов. Поскольку отслеживать траектории движения каждого иона в...
-
Оптическая система - Применение ионного микроскопа
Схема колонны СГИМ Для фокусировки и отклонения ионного пучка используется электростатическая оптическая схема, аналогичная системам со сфокусированным...
-
Назначение. Конструктивные элементы - Выбор вида шланга для применения в конкретном производстве
Гибкие шланг ЕS предназначены для надежного крепления на трубопроводе и исключения передачи вибрации от горелок к газовому тракту. Использование гибких...
-
Введение - Методика конструирования узлов и деталей винтового подъемника
Актуальность выбранной темы. Важную роль на уроках труда, черчения и др. предметов, в школе играют наглядные средства обучения. Они служат для более...
-
Область применения социальных сталей - Понятие и виды спецсталей
Стали и сплавы специального назначения благодаря своим уникальным свойствам находят широкое применение в электроэнергетике, станкостроении,...
-
Что такое чугун? Применения чугуна. - Чугун и сталь
Чугун -- сплав Fe (основа) с С (обычно 0...0 %), содержащий постоянные примеси (Si, Mn, S, Р), а иногда и легирующие элементы (Cr, Ni, V. А0 и др.); как...
-
Назначение, область применения и место установки в производственном процессе Шнековый питатель ПШМ - 1 входит в состав аэрозоль транспортера и...
-
Ассортимент получаемых продуктов и их применение - Промышленные установки нефти и газа
Нефтеперерабатывающая промышленность обеспечивает потребность народного хозяйства в горючих и смазочных материалах. Кроме того, нефть расходуется на...
-
ЦЕЛЕСООБРАЗНАЯ ОБЛАСТЬ ПРИМЕНЕНИЯ - Абсорбционные холодильные машины
Основное преимущество работающих на природном газе АБХМ - сокращение эксплуатационных расходов за счет сокращения потребления относительно дорогостоящей...
-
Области применения абсорбционных процессов - Абсорбер для очистки газов от диоксида углерода
Некоторые из этих областей указаны ниже: 1. Получение готового продукта путем поглощения газа жидкостью. Примерами могут служить: абсорбция SO3 в...
-
Промышленные аккумуляторы, Применение - Принцип действия и использование аккумуляторов
Положительные пластины при производстве промышленных аккумуляторов покрывают толстым слоем перекиси свинца. Отрицательные пластины изготавливаются из...
-
Химические свойства - Целюллоза и ее применение
Химические свойства целлюлозы определяются прежде всего присутствием гидроксильных групп. Действуя металлическим натрием, можно получить алкоголят...
-
Строение, Физические свойства - Целюллоза и ее применение
Молекулярная формула целлюлозы (-C6H10O5-) N, как и у крахмала. Целлюлоза тоже является природным полимером. Ее макромолекула состоит из многих остатков...
Применение математики в конструировании одежды