Циклические коды - Техника передачи дискретных сообщений
Широкое распространение получил класс линейных кодов которые называются циклическими. Название этих кодов происходит от их основного свойства: если кодовая комбинация A1, а2,......, aN-1, aN принадлежит циклическому коду, то комбинации aN, a1, А2,........, aN-1; aN-1, aN, a1, а2,......., аN-2 и т. д., полученные циклической перестановкой элементов, также принадлежат этому коду.
Общим свойством всех разрешенных КК ЦК (как полиномов) является их делимость без остатка на некоторый выбранный полином, называемый производящим. Синдромом ошибки в этих кодах является наличие остатка от деления принятой КК на этот полином. Описание циклических кодов и их построения обычно проводят с помощью многочленов (полиномов). Цифры двоичного кода можно рассматривать как коэффициенты многочлена переменной х. Поскольку любое число в произвольной системе счисления можно записать в виде
,
Где Х-основание системы счисления, AN-1,...,a0 - цифры этой системы, то переход от двоичного числа к записи в виде многочлена осуществляется следующим образом:
1101 1х3 +1х2+1x0=x3+x2+1
KK ЦК описываются полиномами обладающими определенными свойствами. Последние определяются свойствами и операциями той алгебраической системы, к которой принадлежит множество полиномов. Например, в алгебраической системе, которая носит название поля Галуа (GF(x)), действие над коэффициентами полиномов (сложение, вычитание) производится по модулю два. Умножение полиномов должно производиться по модулю некоторого полинома Рr(х). Эти два условия определяют замкнутость указанных операций: их применение не приводит к кодовым комбинациям, длинна которых больше длинны заданного кода n.
Способы формирования циклических кодов.
Найдем алгоритмы построения циклического кода, удовлетворяющего перечисленным выше условиям. Задан полином
,
Определяющий исправляющую способность кода, и задан исходный простой код, который требуется преобразовать в корректирующий циклический. Обозначим многочлен, соответствующий комбинации простого кода, Q(x). Возьмем произведение Q(x)хr и разделим его на P(x). В результате получим многочлен G(x) и остаток R(x)/P(x):
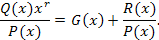
Умножим левую и правую части на P(x). В результате получим:
Перепишем равенство ( * ) в виде
Левая часть (**) делится без остатка на, значит, без остатка делится и правая часть. Таким образом, мы получили два способа формирования кодовых комбинаций циклического кода:
- 1. Путем умножения многочлена исходной кодовой комбинации на производящий полином; 2. Путем деления на производящий полином и приписывания к остатка от деления.
Недостатком первого способа является то, что в результате мы получаем неразделимый код (невозможно отделить проверочные элементы от информационных). Поэтому на практике чаще всего применяется второй способ формирования кодовых комбинаций.
Для обнаружения ошибок в принятой кодовой комбинации достаточно поделить ее на производящий полином. Если принятая кодовая комбинация разрешенная, то остаток от деления будет нулевым. Ненулевой остаток свидетельствует о том, что принятая кодовая комбинация содержит ошибки. По виду остатка (синдрома) можно в некоторых случаях также сделать вывод о характере ошибки и исправить ее.
Похожие статьи
-
Формирование кодовой комбинации циклического кода (Задачи) - Техника передачи дискретных сообщений
3.4.1 Записать кодовую комбинацию циклического кода, если задан производящий полином P(х) = x3+x2+1 и кодовая комбинация, поступающая от источника...
-
Системы ПДС с ОС, Классификация систем с ОС - Техника передачи дискретных сообщений
Классификация систем с ОС В системах с ОС ввод в передаваемую информацию избыточности производится с учетом состояния дискретного канала. С ухудшением...
-
Рис. 4.2.1. Временная диаграмма работы системы с РОС-ОЖ Расчет параметров систем с ОС и ожиданием 4.3.1 Построить временные диаграммы для системы с...
-
Кодирование в системах ПДС, Классификация кодов - Техника передачи дискретных сообщений
Классификация кодов Эффективное кодирование - это процедуры направленные на устранение избыточности (т. е. минимизировать количество элементов,...
-
Циклические коды - Основы построения телекоммуникационных систем и сетей
Широкое распространение получил класс линейных кодов которые называются циклическими. Название этих кодов происходит от их основного свойства: если...
-
ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ - Расчет параметров системы передачи дискретных сообщений
В связи с тем, что при приеме сообщений необходимо обеспечить вероятность ошибки не более 10-6 , используются помехоустойчивые коды, исправляющая и...
-
Эффективное кодирование - Техника передачи дискретных сообщений
Эффективное кодирование - это процедуры направленные на устранение избыточности. Основная задача эффективного кодирования: обеспечить, в среднем,...
-
При организации самостоятельной сети АТ нагрузку каналов в ЧНН между проектируемой и i-й станциями можно представить в следующем виде, Эрл , (23) Общий...
-
Найдем значение соотношения сигнал/шум на выходе согласованного фильтра: Подставим в формулу вычисления вероятности ошибки полученное значение:...
-
ВВЕДЕНИЕ - Расчет параметров системы передачи дискретных сообщений
Электросвязь - это совокупность человеческой деятельности, главным образом технической, связанной с передачей сообщений на расстояние с помощью...
-
2.4.1 Коэффициент нестабильности задающего генератора устройства синхронизации и передатчика k=10-4. Исправляющая способность приемника µ=52%. Краевые...
-
Классификация систем синхронизации Синхронизация есть процесс установления и поддержания определенных временных соотношений между двумя и более...
-
ЛИТЕРАТУРА - Расчет параметров системы передачи дискретных сообщений
Передача дискретных сообщений: учебник для вузов/Под ред. Б. П. Шувалова. М.: Радио и связь, 1990. Чернега B. C. и др. Расчет и проектирование...
-
Время доставки сообщения Тд получателю складывается из времени установления цикловой tцc синхронизации, времени передачи сообщения tпр, времени...
-
Заключение, Список литературы - Техника передачи дискретных сообщений
В данной курсовой работе рассматривались основные принципы системы ПДС. Были рассмотренные взаимозависимости различных параметров характеризующих систему...
-
Теоретические основы Сигнал, поступающий с выхода канала постоянного тока (КПТ), должен быть отождествлен на приемной стороне с "0" или "1". Необходимо...
-
Среднесуточная нагрузка проектируемой станции АТ зависит от потока телеграфного обмена местных и иногородних абонентов. Среднесуточная нагрузка местных...
-
При расчетах каналов и оборудования телеграфных станций сети ПС необходимо учитывать не только нагрузку по передаче и приему телеграмм, но и нагрузку в...
-
Основным типом каналов телеграфной связи на железнодорожном транспорте являются каналы тонального телеграфирования. Они могут быть организованы по...
-
H2 = , Отсюда получим h = 1.79 Рассчитаем вероятность неправильного принятия решения в рассматриваемом приемнике (ДЧМ, КГ). Воспользуемся формулой...
-
Данные передача сигнал сообщение Для обеспечения заданной достоверности при передаче данных применяют обратные связи и помехоустойчивое кодирование,...
-
В качестве основного параметра, характеризующего канал связи, используется вероятность ошибки р в зависимости от отношения h средних мощностей сигнала Wс...
-
Для передачи непрерывных сообщений можно воспользоваться дискретным каналом. При этом необходимо преобразовать непрерывное сообщение в цифровой сигнал,...
-
Расчет количества резервных каналов связи по направлениям - Передача дискретных сообщений
Коэффициент готовности пучка каналов связи определяется по формуле (если каждого канала по направлению равны) , (34) Где - количество каналов в пучке...
-
Для определения необходимого числа каналов на участках между проектируемой станцией и заданными узлами связи дороги воспользуемся номограммой. Процент...
-
1. Шаг коррекции ( Дц ) - смещение фазы ТИ в долях единичного интервала ( Ф 0 ) на выходе делителя частоты (ДЧ) при добавлении или вычитании одного...
-
Определение потока телеграфного обмена по системе прямых соединений - Передача дискретных сообщений
Общий среднесуточный поток телеграфного обмена по каналам системы ПС проектируемой станции определяется из выражения QКпс =, (7) Где n - число станций, с...
-
Введение - Передача дискретных сообщений
Железнодорожный транспорт - вид наземного рельсового транспорта, представляющий собой совокупность его коммуникаций и транспортных средств,...
-
Преобразование в АЦП состоит из трех операций: сначала непрерывное сообщение подвергается дискретизации по времени через интервалы ; полученные отсчеты...
-
Заключение, Литература - Передача дискретных сообщений
В ходе выполнения данной курсовой работы был проведен расчет нагрузки станции абонентского телеграфирования, потока телеграфного обмена по системе прямых...
-
СТРУКТУРНАЯ СХЕМА СИСТЕМЫ СВЯЗИ - Проект обобщенной структурной схемы системы передачи сообщений
Под системой электросвязи понимают совокупность технических средств и среды распространения сигналов, обеспечивающих передачу сообщения от источника к...
-
ВВЕДЕНИЕ - Проект обобщенной структурной схемы системы передачи сообщений
Теория электрической связи (ТЭС), можно сказать, является первым специальным курсом, который ведет к дальнейшему изучению специальности. ТЭС -...
-
ПОВЫШЕНИЕ ВЕРНОСТИ ПРИНИМАЕМЫХ СООБЩЕНИЙ - Расчет параметров системы передачи дискретных сообщений
Существуют два метода повышения верности принимаемых сообщений. Первый метод основан на улучшении качественных показателей каналов, что достигается...
-
Определение сметной стоимости строительства узла коммутации - Передача дискретных сообщений
При определении денежных и материальных затрат на строительство или реконструкцию сооружений электрической связи на стадии проектного задания...
-
Коэффициенты неравномерности и прироста телеграфной нагрузки - Передача дискретных сообщений
Одной из основных особенностей телеграфной связи является неравномерность поступления сообщений, которая обусловлена графиком движения поездов, дневной...
-
В соответствии с исходными данными варианта в качестве приемника применяется приемник когерентного приема ДЧМ. Рассмотрим выражение временной функции...
-
Объектом расчета является цифровая система передачи непрерывных сообщений с импульсно-кодовой модуляцией (ЦСП с ИКМ) по каналу с шумом. Структурная схема...
-
Задача8 Чему равна пропускная способность канала связи, описанного следующей матрицей: ? Решение Найдем безусловные вероятности источника и приемника:...
-
Техника безопасности - Ремонт коробки передач автомобиля на примере ВАЗ-2115
1. Любые работы по ремонту и техническому обслуживанию автомобиля необходимо проводить в просторном, хорошо вентилируемом и освещенном помещении. 2....
-
Охрана труда Перед началом работы нужно: ) Убедиться в исправности спецодежды, обуви и защитных средств. ) Проверить свое рабочее место и место...
Циклические коды - Техника передачи дискретных сообщений