Возмущения от тессеральных и секториальных гармоник, Постановка задачи - Движение искусственного спутника Земли в нецентральном поле тяготения
Постановка задачи
Долготная часть потенциала земного притяжения дается следующей формулой:
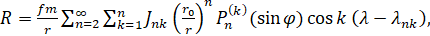
(6.1.1)
Где r -- радиус-вектор;
-- геоцентрическая широта;
-- долгота, отсчитываемая от гринвичского меридиана;
-- присоединенная функция Лежандра;
и -- постоянные.
Как и в случае зональных гармоник, в выражении Rчерез элементы р, е, i, ?, и, v мы будем пренебрегать периодическими членами, пропорциональными. Поэтому будем считать, что в формуле (6.1.1) величины r, sin и равны
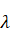
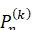
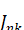
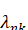
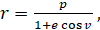
(6.1.2)
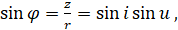
(6.1.3)
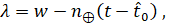
(6.1.4)
(6.1.5)
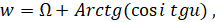
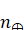
Где через обозначена угловая скорость вращения Земли;
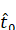
А через -- момент времени, когда гринвичский меридиан проходит через точку весеннего равноденствия.
Посмотрим теперь, как можно выразить функцию R через элементы промежуточного движения. Для этого рассмотрим сначала вторую секториальную гармонику
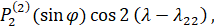
Имеем
(6.1.6)
Пусть
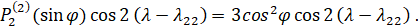
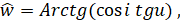
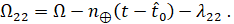
(6.1.7)
Тогда согласно (6.1.4) и (6.1.5)
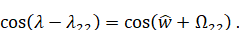
Но поскольку
То
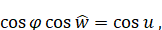
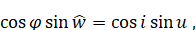
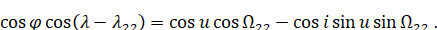
(6.1.8)
Аналогично находим
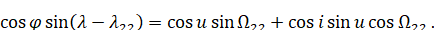
(6.1.9)
Подставляя (6.1.8) и (6.1.9) в (6.1.6) и вводя вместо и переменную и* = и -- 90°, получим
(6.1.10)
Где
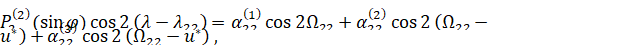
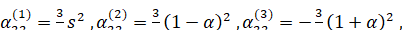
(6.1.11)
Причем
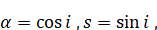
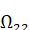
A определяется формулой (6.1.7).
В промежуточном движении мы, очевидно, имеем
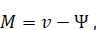
(6.1.12)
Где
(6.1.13)
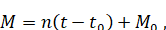
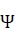
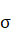
А, если отбросить периодические члены с и, есть уравнение центра, т. е.
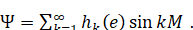
Подставляя в (6.1.7) вместо t его выражение из (6.1.12) и (6.1.13), получим
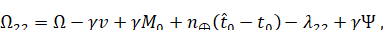
(6.1.14)
Где
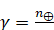
(6.1.15)
Есть отношение угловой скорости вращения Земли к среднему аномалистическому движению спутника.

Сначала мы рассмотрим лишь случай близких спутников, когда величина мала. При этом в разложении функции R будем пренебрегать членами, пропорциональными, т. е. членами порядка. Вследствие этого можно считать, что
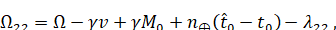
(6.1.16)
Поскольку есть периодическая функция v.
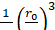
Вторая секториальная гармоника, как показывает формула (6.1.1), имеет множителем величину. Ноприлюбом целом п мы имеем
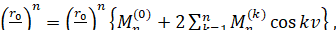
(6.1.17)
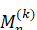
Где суть функции е.
Формулы (6.1.10) (6.1.16) и (6.1.17) показывают, что в случае второй секториальной гармоники функция R будет содержать члены вида
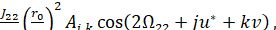
(6.1.18)
Где j и k -- целые числа.
Подобные члены будут содержать и функции R', F' и Ф'.
Поскольку в промежуточном движении
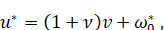
Где и -- постоянные, то, интегрируя члены вида (6.1.18), мы получим
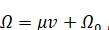
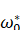
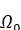
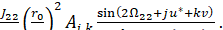
(6.1.19)
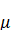
Рассмотрим знаменатель выражения (6.1.19), в котором v и суть величины порядка. Он может быть мал в двух случаях:
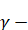
1 малоиj + k = 0 ,
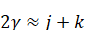
2 .
Очевидно, первый случай соответствует близким спутникам, а второй -- спутникам, периоды обращения которых равны 12H, 24H и. т. д.
Здесь мы ограничимся рассмотрением первого случая. Таким образом, мы будем учитывать только долгопериодические возмущения, для которых j + k = 0. Тогда функции R', F' и Ф' принимают весьма простой вид. Так, например
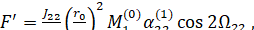
(6.1.20)
Причем
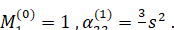
(6.1.21)
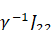
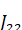
Амплитуды долгопериодических возмущений будут иметь порядок. Короткопериодические возмущения, которыми мы пренебрегаем, пропорциональны. [19]
Похожие статьи
-
Возмущающая функция В этой главе мы рассмотрим возмущения элементов орбиты спутника, обусловленные зональными гармониками потенциала притяжения Земли....
-
Представим возмущающую функцию в следующем виде: (6.2.1) Где (6.2.2) (6.2.3) В формулах (6.2.1) и (6.2.2) первые строчки соответствуют четным h -- q, а...
-
Полученные дифференциальные уравнения для элементов промежуточной орбиты позволяют довольно просто построить аналитическую теорию движения спутника со...
-
Сводка формул для возмущений - Движение искусственного спутника Земли в нецентральном поле тяготения
Приведем окончательные формулы для возмущений элементов промежуточной орбиты. Поскольку v отличается от только периодическими членами порядка и, то с...
-
Рассмотрим, наконец, общую схему вычисления возмущенных координат спутника. Элементы орбиты. Примем за основную систему произвольных постоянных теории...
-
Влияние электромагнитных сил - Движение искусственного спутника Земли в нецентральном поле тяготения
Пусть спутник обладает электрическим зарядом, равным Q. Тогда при движении в магнитном поле Земли на него будет действовать сила F, определяемая формулой...
-
4.1 Введение В предыдущих главах было подробно изучено промежуточное движение искусственного спутника. Была рассмотрена качественная картина движения,...
-
Замечания - Движение искусственного спутника Земли в нецентральном поле тяготения
Представление потенциала притяжения Земли в виде ряда по сферическим функциям стало классическим. В силу простоты сферических функций оно очень удобно...
-
В этой части мы сведем дифференциальные уравнения (2.1.6) к квадратурам, которые и будут в дальнейшем использованы для построения промежуточной орбиты...
-
2.1 Дифференциальные уравнения движения искусственного спутника Мы ввели подвижную, жестко связанную с Землей, систему координат и соответствующие ей...
-
Введение В предыдущих главах были рассмотрены возмущения элементов орбиты спутника, вызываемые зональными и тессеральными гармониками геопотенциала и...
-
Постановка задачи В этой главе мы рассмотрим возмущения в движении спутника, обусловленные притяжением Луны и Солнца. Пусть, как и раньше, Оxyz --...
-
ВВЕДЕНИЕ - Движение искусственного спутника Земли в нецентральном поле тяготения
Изучение движения искусственных спутников Земли представляет интерес не только для специалистов по астродинамике, занимающихся прогнозированием движения...
-
Давление света В этом главе мы выведем формулу для возмущающего ускорения, вызываемого действием светового давления на спутник. Сначала мы предположим,...
-
В формулы для возмущений элементов помимо масс и больших полуосей возмущающих тел входят также наклоны, долготы узлов и перигеев Луны и Солнца,...
-
Рассмотрим сначала промежуточное движение. Мы видели, что промежуточное движение спутника происходит в области, ограниченной двумя эллипсоидами и двумя...
-
Введение Помимо несферичности Земли, притяжения Луны и Солнца, сопротивления атмосферы и светового давления на движение спутника действует целый ряд...
-
Из дифференциальных уравнений и формул видно, что элементы L, G, Н, а следовательно, и а, е, i, не имеют (по крайней мере в первом приближении) вековых...
-
Эллиптические функции Якоби В предыдущей главе были найдены первые интегралы уравнений промежуточного движения, позволяющие записать общий интеграл...
-
Рассмотрим распределение силы тяжести на уровенной поверхности. Ускорение силы тяжести gдается формулой (1.2.1) Где Так как второе слагаемое правой части...
-
Плотность атмосферы - Движение искусственного спутника Земли в нецентральном поле тяготения
Плотность воздуха верхней атмосферы определяется как непосредственно, при помощи аппаратуры, установленной на спутниках и ракетах, так и косвенным путем,...
-
Сила сопротивления атмосферы - Движение искусственного спутника Земли в нецентральном поле тяготения
При изучении поступательного движения спутника принимают во внимание лишь ту компоненту аэродинамических сил, направление которой противоположно вектору...
-
В предыдущих главах были выведены формулы, позволяющие вычислять положение спутника в пространстве для любого момента времени, если известны численные...
-
Притяжение объемного тела - Движение искусственного спутника Земли в нецентральном поле тяготения
Рассмотрим задачу о притяжении материальной точки Р единичной массы некоторым телом М. Будем предполагать, что тело имеет произвольную форму, а плотность...
-
Рельеф лунной поверхности, Движение луны - Луна как спутник Земли
Граница дня и ночи на Луне называется терминатором, в это время лучше всего изучать рельеф Луны, потому что все неровности отбрасывают тень и их легко...
-
Нецентральность гравитационного поля Земли - Возмущенное движение космического аппарата
Возмущенный движение гравитационный орбита При решении ограниченной задачи двух тел Земля представляется шаром со сферическим распределением плотности. В...
-
Покажем, что для любой классической системы, обладающей центральной симметрией и заданной энергией, существует такая метрика, что действие системы будет...
-
Закон Всемирного тяготения - Законы движения небесных тел и строение Солнечной системы
Законы Кеплера прекрасно описывали наблюдаемое движение планет, но не вскрывали причин, приводящих к такому движению (напр. вполне можно было считать,...
-
" Наука совершенствуется опытом " Фрэнсис Бэкон (1561 - 1626) Все существующие космические летательные аппараты передвигаются за счет инерции,...
-
Сравнивая дуги, на которые перемещаются планеты за равные промежутки времени, установить, какая из планет быстрее движется на звездном небе, и объяснить...
-
Запуск второго искусственного спутника Земли - История развития космонавтики
Работы по созданию второго искусственного спутника Земли начались сразу после запуска первого, и уже 12 октября 1957 г. было принято официальное решение...
-
Запуск первого искусственного спутника Земли - История развития космонавтики
4 октября 1957 г. весь мир потрясло известие о том, что на околоземную орбиту выведен первый советский искусственный спутник Земли "Спутник-1". Так был...
-
В 1955 году (задолго до летных испытаний ракеты Р-7) С. П. Королев, М. В. Келдыш, М. К. Тихонравов вышли в правительство с предложением о выведении в...
-
Путь, описываемый космическим аппаратом в пространстве наз. траекторией. Прямолинейные траектории. Если начальная скорость равна нулю, то тело начинает...
-
Параболическое движение, Прямолинейное движение - Математическое моделирование движения небесных тел
(p = 0, e = 1) Уравнение параболической орбиты записывают в видеp r = 1 + cos v (1.80) Где величина определяет расстояние от центра притяжения M0 до...
-
Введение - Аномальное движение орбит в общей теории относительности
Как известно, в общей теории относительности можно определить аномальное движение орбит [1]. Для решения задачи о вековом аномальном смещении перигелия...
-
Магнитное поле Нептуна, Нептун и его кольца, Спутники и кольца Нептуна - Планета Нептун
Нептун и его кольца Регулярные радиовсплески, обнаруженные "Вояджером-2", говорят о том, что Нептун имеет магнитное поле и окружен магнитосферой....
-
Погода на завтра - что может быть актуальнее для каждого из нас. Мы можем без особого внимания прослушать программу новостей, но как только начинают...
-
В чем смысл открытого физического феномена? - Как движение Земли влияет на погоду, приливы и отливы
Представьте себе два груза из стали в форме шара, больший шар имеет массу 2 кг., а меньший шар имеет массу 1 кг. Если поднять шар 1, который имеет массу...
-
Устройство выглядит так: на корпусе 1 установлен двигатель 2, который работает от электричества и управляется пультом 3. Пульт 3 выполняет функцию...
Возмущения от тессеральных и секториальных гармоник, Постановка задачи - Движение искусственного спутника Земли в нецентральном поле тяготения