Изотонная звездная сходимость
Данная работа продолжает систематическое изучение свойств звездных сходимостей, проводившееся в работах [1-3]. Наряду с конфинальными, муровскими, квазиподсетями есть еще один класс подсетей - изотонные [4]. Применив его к общей концепции звездных сходимостей в пространствах абстрактной сходимости, получаем еще один тип звездной сходимости - изотонную звездную сходимость.
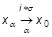
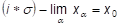
Пусть - пространство - сходимости. Будем говорить, что сеть изотонно звездно сходится к точке, если каждая ее изотонная подсеть имеет свою изотонную подсеть, которая - сходится к точке. Запись: или.
Первый, возникающий после введения данного понятия, вопрос - это, в каком отношении эта сходимость находится с ранее введенными [1-3] типами звездных сходимостей? Из соотношений основных классов подсетей [4] получается:
Теорема 1
.
Для дальнейшего нам понадобится следующий результат.
Лемма. Отношение "быть изотонной подсетью сети..." транзитивно на множестве всех сетей данного пространства абстрактной сходимости.
Доказательство. Пусть сеть есть изотонная подсеть сети, а сеть есть изотонная подсеть сети. Покажем, что сеть есть изотонная подсеть сети. По условию существуют отображения и такие, что выполнены условия:
- 1.1 , т. е. . 1.2 . 1.3 изотонно. 2.1 , т. е. . 2.2 . 2.3 изотонно.
Построим функцию по правилу. Тогда для каждого будет, значит, т. е. . Таким образом, и первое условие изотонной подсети выполнено. Далее, зададим любое, по условию (1.2) найдем соответствующее ему такое, что. По условию (2.2) для найдем такое, что. Тогда при будет, далее, следовательно, . Итак, при будет, т. е. и выполнено второе условие изотонной подсети. Наконец, проверим изотонность отображения. Пусть. По (2.3) . По (1.3) , т. е. и - изотонно. В итоге, сеть есть изотонная подсеть сети.
Лемма доказана.
Обратимся теперь к изучению свойств изотонной звездной сходимости. В частности, нас будут интересовать свойства, связанные с аксиомами Дж. Келли класса сходимости.
Теорема 2 - сходимость имеет свойство NA2.
Доказательство. Пусть сеть изотонно звездно сходится к, - любая ее изотонная подсеть. Рассмотрим любую ее изотонную подсеть. В силу леммы - изотонная подсеть. Из - сходимости к получаем, что имеет изотонную подсеть, которая - сходится к. В силу леммы есть изотонная подсеть сети. Таким образом, каждая изотонная подсеть сети имеет изотонную подсеть, - сходящуюся к. Это и означает - сходимость сети к точке.
Теорема доказана.
Теорема 3 - сходимость имеет свойство NA3.
Доказательство. Пусть сеть не сходится изотонно звездно к. Допустим, что каждая ее изотонная подсеть имеет изотонную подсеть, - сходящуюся к. Тогда каждая изотонная подсеть сети имеет изотонную подсеть, - сходящуюся к. В силу леммы сеть есть изотонная подсеть сети. Это означает изотонную звездную сходимость к. Противоречие.
Теорема доказана.
Теорема 4 Если - сходимость удовлетворяет условию NA1, то ему удовлетворяет и - сходимость.
Доказательство. Пусть NA1 выполнено для. Рассмотрим любую изотонную подсеть сети и далее любую изотонную подсеть сети. В силу леммы - изотонная подсеть сети. Таким образом, существует отображение :
- 1 . 2 . 3 - изотонно.
Из условия (1) следует, что. Тогда - сходится к, а это означает - сходимость сети к.
Теорема доказана.
Исследуем соотношение сходимостей и.
Теорема 5 Если - сходимость удовлетворяет условию NA2, то
.
Доказательство. Пусть NA2 для выполнено, сеть - сходится к, - любая ее изотонная подсеть, - любая изотонная подсеть сети. В силу леммы есть изотонная подсеть. В силу NA2 - сходится к. Это означает - сходимость сети к.
Теорема доказана.
Теорема 6 Если - сходимость удовлетворяет NA3, то.
Доказательство. Пусть условие NA3 выполнено для, сеть - сходится к. Допустим, что не сходится к. В силу NA3 имеет такую изотонную подсеть, у которой все изотонные подсети не сходятся к. Но тогда не может - сходится к. Противоречие.
Теорема доказана.
Теорема 7 Данная сходимость совпадает с изотонно звездной к ней тогда и только тогда, когда удовлетворяет NA2 и NA3.
Этот результат вытекает из теорем 5 и 6.
Теорема 8
.
Вытекает из теорем 2,3,7.
Теорема 9 Если на заданы сходимости и и, то
.
Доказательство. Пусть сеть - сходится к. Тогда любая ее изотонная подсеть имеет изотонную подсеть, - сходящуюся к. В силу условия теоремы - сходится к, что и дает - сходимость к.
Теорема доказана.
Если в формулировках аксиом класса сходимости использовать изотонные подсети, то можно провести модификацию третьей аксиомы.
Теорема 10 Аксиома эквивалентна аксиоме NA3.1. .
Доказательство.
1 При выполнении для в силу теоремы 6 NA3.1 выполнено.
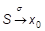
2 При выполнении NA3.1 допустим существование сети, для которой NA3 не выполнена. Тогда каждая изотонная ее подсеть имеет свою изотонную подсеть, которая - сходится к. Это дает - сходимость к. В силу NA3.1 получаем, что невозможно.
Теорема доказана.
SUMMARY
The properties of the fourth type star convergence have been explored. The connections between this convergence and the convergence class axioms have been investigated.
СПИСОК ЛИТЕРАТУРЫ
Погребной В. Д. Конфинальная звездная сходимость //Вісник Сумського державного університету. - 2001. - №4(25). - С.141-144.
Погребной В. Д. Муровская звездная сходимость //Вісник Сумського державного університету. - 2002. - №5(38). - С.180-183.
Погребной В. Д. Квазизвездная сходимость //Вісник Сумського державного університету. - 2002. - №6(39). - С.183-186.
Погребной В. Д. Основные классы подсетей //Вісник Сумського державного університету. - 2001. - №3(24). - С.138-140.
Похожие статьи
-
Метод звездных подсчетов - Научные представления о строении Вселенной
Данные о крупномасштабной структуре 2df обзора Первым способом изучения крупномасштабной структуры Вселенной, не потерявший своей актуальности, стал так...
-
Для сравнение с теоретическими данным сырые данные приводятся к вращательно-инвариантной величине: "Спектр" же строят для величины l(l+1)Cl/2р, из...
-
Светимость звезд, звездная величина - Физика звезд
Если смотреть на звездное небо, сразу бросается в глаза, что звезды резко отличаются по своей яркости - одни светят очень ярко, они легко заметны, другие...
-
В КОГО ЦЕЛИТСЯ ЗВЕЗДНЫЙ СТРЕЛЕЦ - Созвездия зодиака
240-270° эклиптики. Большое созвездие из звезд 3-й, 4-й, 5-й и двух звезд 2-й величины. Лежит в области, богатой звездными скоплениями и туманностями....
-
Основные звездные характеристики, Светимость и расстояние до звезд - Жизненный путь звезды
Чтобы любоваться звездным небосводом, совсем не обязательно описывать все звезды и выяснять их физические характеристики - они красивы сами по себе. Но...
-
Введение, Основные звездные характеристики, Светимость - Звезды. Их рождение, жизнь и смерть
Как и все тела в природе, звезды не остаются неизменными, они рождаются, эволюционируют и умирают. Чтобы проследить жизненный путь звезды и понять, как...
-
Метагалактика - Звездные системы галактики
Понятие " Метагалактика " не является вполне ясным. Оно сформировалось на основании аналогии со звездами. Наблюдения показывают, что галактики, подобно...
-
ЗВЕЗДНЫЙ СТРЕЛЕЦ - Созвездия звездного неба
240 - 270° эклиптики. Большое созвездие из звезд 3-й, 4-й, 5-й и двух звезд 2-й величины. Лежит в области, богатой звездными скоплениями и туманностями....
-
Звездные скопления - Космические объекты
По-видимому, почти все звезды рождаются группами, а не по отдельности. Поэтому нет ничего удивительного в том, что звездные скопления -- вещь весьма...
-
Межзвездная пыль - Основные звездные характеристики. Рождение звезд
До сих пор, говоря о межзвездной среде, мы имели ввиду только межзвездный газ. но имеется и другая компонента. Речь идет о межзвездной пыли. Мы уже...
-
Стадии звездной эволюции - Эволюция и строение звезд
Этот процесс является закономерным, то есть неизбежным. В самом деле, тепловая неустойчивость межзвездной среды неизбежно ведет к ее фрагментации, то...
-
Магнитное поле звезд, Пузырь звездного ветра - Физика звезд
Звездное магнитное поле -- Магнитное поле , создаваемое движением проводящей Плазмы внутри звезд Главной последовательности . Это движение создается...
-
КОЗЕРОГ - Созвездия звездного неба
270 - 300° эклиптики. Созвездие состоит из звезд не ярче 3-й величины. На "лбу" этого иероглифического животного главная звезда Гиеди - двойная. Каждая...
-
Звездная астрономия, Космогония - Структура астрономии как научной дисциплины
Изучение звезд и звездной эволюции имеет фундаментальное значение для нашего понимания Вселенной. Астрофизика звезд развивалась на основе наблюдений и...
-
ЛЕВ - Созвездия звездного неба
120 - 150° эклиптики. Занимает большую область неба. Звезды 1-й, 2-й, 3-й, 4-й, 5-й величин. Звезда 1-й величины - Регул, или Сердце Льва, голубая,...
-
Созвездия звездного неба - Созвездия звездного неба
В темную, безлунную и безоблачную ночь на небе видно множество звезд. Кажется, трудно разобраться в этой величественной картине звездного неба, о которой...
-
Галактики - это большие звездные системы, в которых звезды связаны друг с другом силами гравитации. Существуют галактики, включающие триллионы звезд....
-
Кратко о всем процессе рождения - Основные звездные характеристики. Рождение звезд
Мы довольно подробно рассматривали вопрос о конденсации в протозвезды плотных холодных молекулярных облаков, на которые из-за гравитационной...
-
Звездные скопления - Процесс образования и структура звезд
По-видимому, почти все звезды рождаются группами, а не по отдельности. Поэтому нет ничего удивительного в том, что звездные скопления - вещь весьма...
-
В кого целится звездный стрелец - Звездное небо
По древнегреческой мифологии мудрейший из кентавров Хирон, сын бога Хроноса и богини Фемиды, создал и первую модель небесной сферы. При этом одно место в...
-
Изменение вида звездного неба в течение года
Изменение вида звездного неба в течение года Цель : Познакомится с экваториальной системой координат, видимым годичным движениям Солнца и видам звездного...
-
Температура поверхности Солнца - Звездное небо
Когда стал известен Химический состав Солнца, число ядерных реакций, которые могли бы служить возможным источником огромного количества вырабатываемой...
-
Исключительно богатую информацию дает изучение спектров звезд. Уже давно спектры подавляющего большинства звезд разделены на классы. Последовательность...
-
Движение планет - Изучение звездного неба на Древнем Востоке
Наблюдая за годичным перемещением Солнца среди звезд, древние люди научились заблаговременно определять наступление того или иного времени года. Они...
-
Звездные дожди - Малые тела Солнечной системы
Когда астероид или комета распадаются на части, их обломки рассеиваются на прежней орбите. Если ее пересекает Земля, происходит так называемый звездный...
-
Изменение вида звездного неба в течение суток
Тема: Изменение вида звездного неба в течение суток Цель: Познакомить учащихся с небесной средой и ее вращением, ориентировкой по небу. Рассмотреть...
-
Природа постоянства скорости света - Звездная аберрация против релятивистской астрономии
Два варианта могут объяснить постоянство скорости света. Первый вариант. Существуют "жесткие" и "эластичные" модели эфира. Атрибутом "жесткой" модели...
-
Виды галактик - Звездные системы галактики
Галактики во Вселенной не похожи друг на друга. Некоторые из них ровные и круглые, другие имеют форму уплощенных разметавшихся спиралей, а у некоторых не...
-
Абсолютные звездные величины - Спектральная классификация звезд типа Вольфа-Райе
Среднюю абсолютную звездную величину звезд WR в Галактике впервые оценил Фаас (1928), сравнив видимые величины звезд WR и соседних звезд О. Оказалось,...
-
Состав нашей Галактики - Звездные системы галактики
Самые маленькие коллективные члены Галактики - это Двойные и кратные звезды . Так называются группы из двух, трех, четырех и более звезд, в которых...
-
Звездные миры. - В поисках системы мира
К началу нашего века границы разведанной Вселенной раздвинулись настолько, что включили в себя Галактику. Многие, если не все, думали тогда, что эта...
-
Связь основных звездных величин, Молодые звездные коллективы - Жизненный путь звезды
Итак, современная астрономия располагает методами определения основных звездных характеристик: светимости, поверхностной температуры (цвета), радиуса,...
-
Строение нашей Галактики - Звездные системы галактики
Важнейшей особенностью небесных тел является их свойство объединяться в системы. Земля и ее спутник Луна образуют систему из двух тел. Так как размеры...
-
Масса галактик - Звездные системы галактики
Не так много лет назад одной из наиболее надежных областей внегалактической астрономии было определение масс галактик. Для этой цели были разработаны...
-
Связь основных звездных величин, Молодые звездные коллективы - Рождение и жизнь звезд
Итак, современная астрономия располагает методами определения основных звездных характеристик: светимости, поверхностной температуры (цвета), радиуса,...
-
Эволюция галактик - Звездные системы галактики
Одна из задач современной астрономии - понять, как образовались галактики и как они эволюционируют. Во времена Эдвина Хаббла и Харлоу Шепли было...
-
Открытые звездные скопления - Звезды
Наверное, самым знаменитым открытым звездным скоплением являются Плеяды, или Семь сестер, в созвездии Тельца. Несмотря на такое название, большинство...
-
Введение - Звездные системы галактики
С древнейших времен людей интересовало, что же находится за горизонтом, и они отправлялись исследовать далекие и незнакомые земли. По мере того как Земля...
-
Звездные миры - Движение планет
К началу нашего века границы разведанной Вселенной раздвинулись настолько, что включили в себя Галактику. Многие, если не все, думали тогда, что эта...
-
Вращательное движение - Звездная аберрация против релятивистской астрономии
Посмотрим, как можно объяснить парадокс Эренфеста, если считать, что пространство является общим для всех инерциальных систем, а время для них едино....
Изотонная звездная сходимость