НЕЧЕТКИЕ ОТНОШЕНИЯ - Статистические методы оценки получаемых знаний учащимися в общеобразовательной средней школе
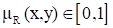
Пусть - прямое произведение универсальных множеств и М - некоторое множество принадлежностей. Нечеткое n-арное отношение определяется как нечеткое подмножество R на E, принимающее свои значения в М. В случае и, нечетким отношением R между множествами и будет называться функция R:(X, Y)® [0,1], которая ставит в соответствие каждой паре элементов (х, y)ОXгY величину. Обозначение: нечеткое отношение на XгY запишется в виде: xОX, yОY: xRy. В случае, когда X = Y, т. е. X и Y совпадают, нечеткое отношение R: XгX®[0,1] называется нечетким отношением на множестве X.
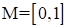
Примеры:
Пусть X = {x1,x2,x3}, Y = {y1,y2,y3,y4}, М = [0,1]. Нечеткое отношение R=XRY может быть задано, к примеру, таблицей:
|
Y1 |
Y2 |
Y3 |
Y4 | |
|
X1 |
0 |
0 |
0,1 |
0,3 |
|
X2 |
0 |
0,8 |
1 |
0,7 |
|
X3 |
1 |
0,5 |
0,6 |
1 |
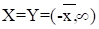
Пусть, т. е. множество всех действительных чисел. Отношение (x много больше y) можно задаеть функцией принадлежности:
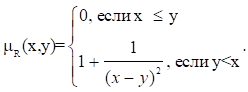
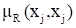
Отношение R, для которого, при достаточно больших k можно интерпретировать так: "x и y близкие друг к другу числа". В случае конечных или счетных универсальных множеств очевидна интерпретация нечеткого отношения в виде нечеткого графа, в котором пара вершин (xi, xj) в случае XRX соединяется ребром с весом, в случае XRY пара вершин (xi, yj) соединяется ребром c весом.
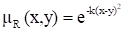
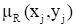
Примеры:
Пусть Х={x1,x2,x3}, и задано нечеткое отношение R: XгX® [0,1], представимое графом:
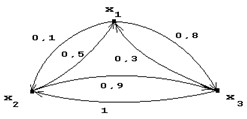
Пусть X={x1,x2} и Y={y1,y2,y3}, тогда нечеткий граф вида:
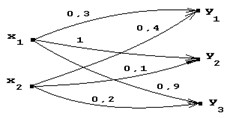
Задает нечеткое отношение XRY.
Замечание. В общем случае нечеткий граф может быть определен на некотором GМXгY, где G - множество упорядоченных пар (x, y) (необязательно всех возможных) такое, что и.
Будем использовать обозначения вместо и вместо.
Пусть.
Носитель нечеткого отношения.
Носителем нечеткого отношения R называется обычное множество упорядоченных пар (x, y), для которых функция принадлежности положительна:
.
Нечеткое отношение содержащее данное нечеткое отношение, или содержащееся в нем.
Пусть R1 и R2 - два нечетких отношения такие, что:
,
Тогда говорят, что R2 содержит R1 или R1 содержится в R2 .
Обозначение: .
Пример:
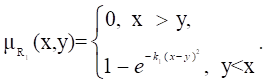
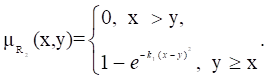
Отношения R1 , R2 - отношения типа (y много больше x). При отношение R2 содержит R1 .
Операции над нечеткими отношениями
Объединение двух отношений и.
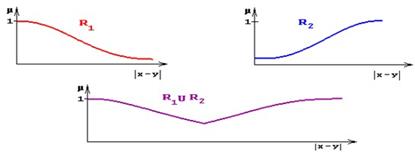
Объединение двух отношений обозначается R1ИR2 и определяется выражением:
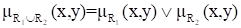
.
Пример:
Ниже изображены отношения действительных чисел, содержательно означающие: xR1y - "числа x и y очень близкие", xR2y - "числа x и y очень различны" и их объединение xR1ИR2y - "числа x и y очень близкие или очень различные".
Функции принадлежности отношений заданы на |y-x|.
Пересечение двух отношений
Пересечение двух отношений R1 и R2 обозначается R1?R2 и определяется выражением:
.
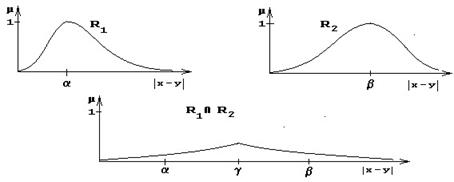
Пример:
Ниже изображены отношения: xR1y, означающее "модуль разности |y-x| близок к a", xR2y, означающее "модуль разности |y-x| близок к b", и их пересечение.
Алгебраическое произведение двух отношений
Алгебраическое произведение двух отношений R1 и R2 обозначается R1ЧR2 и определяется выражением:
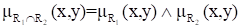
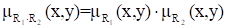
.
Алгебраическая сумма двух отношений
Алгебраическая сумма двух отношений R1 и R2 обозначается R1R2 и определяется выражением:
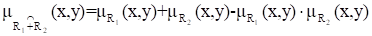
.
Для введенных операций справедливы следующие свойства дистрибутивности:
,
R1И(R2ЗR3) = (R1ИR2)З(R1ИR3),
,
,
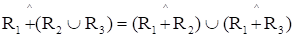
,
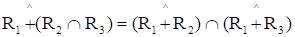
.
Дополнение отношения
Дополнение отношения R обозначается и определяется функцией принадлежности:
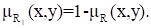
Дизъюнктивная сумма двух отношений
Дизъюнктивная сумма двух отношений R1 и R2 обозначается R?R и определяется выражением:
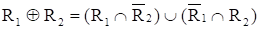
.
Обычное отношение, ближайшее к нечеткому.
Пусть R - нечеткое отношение с функцией принадлежности. Обычное отношение, ближайшее к нечеткому, обозначается R и определяется выражением:
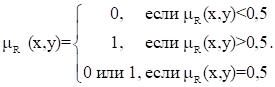
Проекции нечеткого отношения
Пусть R - нечеткое отношение. Первой проекцией отношения R (проекция на X) называется нечеткое множество, заданное на множестве X, с функцией принадлежности:
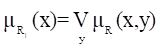
.
Аналогично, второй проекцией (проекцией на Y) называется нечеткое множество, заданное на множестве Y, с функцией принадлежности:
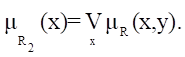
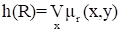
Величина называется глобальной проекцией отношения R. Если h(R)=1, то отношение R нормально, в противном случае - субнормально.
Цилиндрические продолжения проекций нечеткого отношения
Проекции R1 и R2 нечеткого отношения XRY в свою очередь определяют в XгY нечеткие отношения и с функциями принадлежности:
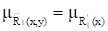
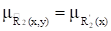
При любом y, при любом x,
Называемые, соответственно, цилиндрическим продолжением и цилиндрическим продолжением.
Замечание. Очевидно, что для любых нечетких подмножеств А и В, определенных, соответственно, на X и Y, можно построить их цилиндрические продолжения А и В.
Сепарабельность отношений
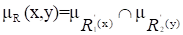
Нечеткое отношение XRY называется сепарабeльным, если оно равно пересечению цилиндрических продолжений своих проекций, т. е. если, т. е. .
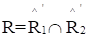
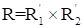
Замечание. Если определено декартово произведение нечетких множеств (выше оно введено), то, очевидно, нечеткое отношение XRY сепарабельно, если оно является декартовым произведением своих проекций, т. е. .
Композиция двух нечетких отношений
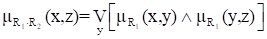
Пусть R1 - нечеткое отношение между X и Y, и R2 - нечеткое отношение между Y и Z. Нечеткое отношение между X и Z, обозначаемое, определенное через R1 и R2 выражением, называется (max-min)-композицией отношений R1 и R2.
Свойства max-min композиции
Операция (max-min)-композиции ассоциативна, т. е.
,
Дистрибутивна относительно объединения, но недистрибутивна относительно пересечения:
,
.
Кроме того, для (max-min)-композиции выполняется следующее важное свойство: если то,.
(max-*) - композиция.
В выражении для (max-min)-композиции отношений R1 и R2 операцию можно заменить любой другой, для которой выполняются те же ограничения, что и для : ассоциативность и монотонность (в смысле неубывания) по каждому аргументу. Тогда:
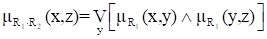
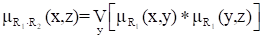
.
В частности, операция может быть заменена алгебраическим умножением, тогда говорят о (max - prod)-композиции.
Обычное подмножество a - уровня нечеткого отношения
Обычным подмножеством a - уровня нечеткого отношения R называется четкое (обычное) отношение Ra такое, что
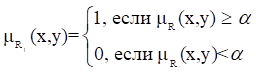
Очевидно, что из a1Ј a2 следует Ra1 і Ra2.
Теорема декомпозиции
Любое нечеткое отношение R представимо в форме:
, 0<aЈ1,
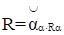
Где aЧRa означает, что все элементы Ra умножаются на a.
Условные нечеткие подмножества.
Пусть X и Y - универсальные множества, взаимосвязь которых задана нечетким отношением, т. е. для каждой пары задано значение функции принадлежности.
Пусть А - некоторое нечеткое множество, заданное на Х, т. е. определена функция принадлежности для всех х из Х. Тогда нечеткое множество А и нечеткое отношение R индуцируют в Y нечеткое подмножество B с функцией принадлежности
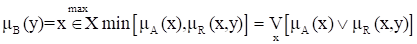
.
Обозначение: .
Немного о бинарных отношениях вида XRX
Нечеткие отношения вида XRX задаются функцией принадлежности ? R(x, y), но с условием, что x и y - элементы одного и того же универсального множества. В зависимости от своих свойств (основные - симметричность, рефлексивность, транзитивность) конкретные нечеткие отношения задают отношения сходства и различия, порядка или слабого порядка между элементами Х. Они имеют обширную сферу приложений в задачах автоматической классификации и принятия решений (сравнение альтернатив).
Похожие статьи
-
НЕЧЕТКИЕ МНОЖЕСТВА Пусть - универсальное множество, - элемент, а - некоторое свойство. Обычное (четкое) подмножество универсального множества E, элементы...
-
Какие бы реформы не проходили в образовании, в конечном итоге они замыкаются на педагоге, которому во все времена принадлежала ведущая роль в воспитании...
-
ОТВЕТ. Математические выражения - это слова письменного математического языка, он относится к искусственным языкам, которые создаются и развиваются с той...
-
Для осуществления организации коммуникативно-интерактивного обучения с целью развития дискутивных навыков у учащихся необходим высокий методический...
-
Анализ УМК Кузовлева В. П. "The World of English" на предмет формирования у учащихся дискутивных умений УМК В. П. Кузовлева, Э. Ш. Перегудовой, Н. М....
-
Ответ. Прием вычисления над N складывается из ряда последовательных операций, выполнение которых приводит к нахождению результата, требуемого...
-
Анализ методической литературы по проблеме формирования положительного отношения младших школьников к учебной деятельности в процессе выполнения домашних...
-
Актуальное состояние педагогической практики по использованию различных форм оценки достижений учащихся на уроках русского языка при изучении темы...
-
Как уже было сказано ранее, тем методом, который способствовал бы развитию активности и самостоятельности школьников, в то же время обеспечил бы...
-
Проектный метод обучения содержит большой потенциал в реализации межпредметных связей: русский язык, литература, природоведение, рисование,...
-
Характеристика сформированности ценностного отношения к природе у первоклассников Констатирующий эксперимент, направленный на выявление сформированности...
-
Контролирование, оценивание знаний, умений обучаемых включаются в диагностирование как необходимые составные части. Это очень древние компоненты...
-
Для реализации коммуникативно-интерактивного подхода наиболее приемлемым представляется обучение на основе дискуссии в форме группового сотрудничества и...
-
Современный этап развития школы характеризуется изменением образовательных ценностей: на смену предметно-ориентированному обучению приходит...
-
Дискутивный интерактивный обучение английский Основные положения коммуникативно-интерактивного обучения В педагогике различают несколько моделей...
-
Прогностическая функция проверки служит получению опережающей информации об учебно-воспитательном процессе. В результате проверки получают основания для...
-
Происходящие в России социальные изменения ставят личность в сложные психологические условия, связанные с процессом изменения общественного сознания. В...
-
Применение данного метода позволяет учителю получить сведения об усвоении того или иного материала, не затрачивая время на беседу с учащимися или на...
-
Оценка достижений учащихся в начальной школе Совершенствование системы начального образования направлено на решение ряда важнейших задач, среди которых...
-
Ответ. Уравнение - это равенство с переменой. Если соединить f(х) и g(х) два выражения с переменной х - и областью определению х, тогда высказывательная...
-
Ценностное отношение как научное понятие Сегодня человечество вынужденно решать глобальные экологические проблемы и выработать такую концепцию...
-
Цель : Познакомить учащихся с отвлеченными и именованными числами, их видами и преобразованиями. Отработка и контроль вычислительных навыков, решение...
-
Методы контроля, п.5.1. Устная проверка - Контроль за качеством знаний на уроке математики
Среди методов контроля выделяют: устную проверку, проверку письменно-графических работ и проверку практических работ. П.5.1. Устная проверка Устная...
-
Ответ. Прием вычисления над данными числами складывается из ряда последних операций, выполнение которых приводит к нахождению результата требуемого...
-
Ответ. Большое значение для первых уроков начальной математики имеет работа над числовым рядом. Рост числового ряда прибавлением по единице удобно...
-
Развитие гражданских и патриотических качеств младших школьников как основы гражданской идентичности на уроках Патриотизм - это любовь к Родине,...
-
Ответ. Понятия, изучаемые в начальной школе, обычно представляют в виде 4-х групп: 1) числа и операции над ними: число, слагаемое, сложение, больше и...
-
Проверка и оценка знаний учащихся на уроке - завершающий этап обучения. Основная цель этой составной части урока - определение качества усвоения...
-
В заключении можно сделать следующие выводы по всему содержанию работы. Характеризуя оценку достижений учащихся в начальной школе, мы отметили, что...
-
Сущность ориентирующей функции контроля - в получении информации о степени достижения цели обучения отдельным учеником и классом в целом - насколько...
-
В отечественной методической системе упражнение рассматривается как : А) структурная единица методической организации учебного материала, Б) единица...
-
В рамках общего экономического образования в начальных классах акцент делается на элементарных понятиях, связанных с жизненным опытом детей....
-
Анализ психолого-педагогической литературы показал, что для решения разнообразных задач с помощью метода проектов можно выделить шесть основных этапов:...
-
В процессе обучения происходит постоянное взаимодействие учителя и учеников. Учение, имеющее ярко выраженную личностную окраску, каждым из учащихся...
-
Учитель трудовой обучение школьник Немного истории о методе проектов Метод проектов не является принципиально новым в мировой практике. Он возник еще в...
-
Введение - Метод проектов и его применение в общеобразовательной школе
Сегодня в условиях информационного общества система накопления фактических знаний, как это было ранее, постепенно заменяется. Новая ситуация требует...
-
Практика преподавания иностранного языка в школе показывает, что изучение иностранного языка при традиционном подходе обычно ассоциируется с нудным,...
-
Арифметический метод решения требует большего умственного напряжения, что положительно сказывается на развитии умственных способностей, матем-ой...
-
Характеристика методов контроля и оценки знаний - Методы контроля и оценки знаний обучающихся
Проверка и контроль успеваемости является составной частью процесса обучения, тесно связан с другими его звеньями: изучение нового материала, его...
-
На современном этапе обучения иностранному языку все большее внимание уделяется формированию творческих составляющих речевой деятельности, а именно:...
НЕЧЕТКИЕ ОТНОШЕНИЯ - Статистические методы оценки получаемых знаний учащимися в общеобразовательной средней школе