Методический аспект развития знаково-символических учебных действий - Схематическое моделирование условия задачи в развитии знаково-символических действий у младших школьников

Наглядно-образный тип мышления младших школьников - психологическая основа развития знаково-символических действий учащихся в обучении решению текстовых задач. Чтобы решить задачу, младших школьников должен визуально представить (увидеть) ее условие и понять взаимосвязи ее данных.

Развитие знаково-символических учебных действий в процессе обучения решению задач имеет строго определенную последовательность, которая определяется системой типов текстовых задач в программе по математике. Представим последовательность моделей в соответствии с типами текстовых задач.

1. Простейшим видом знаково-символической модели условия задачи является рисунок. Эта форма краткой записи условия задачи применяется в 1 классе.

Задача. Мальчик для украшения новогоднего зала вырезал 10 елочек, а девочка 8. Сколько елочек вырезали дети?

Имея наглядное представление задачи на нахождение суммы, первоклассники осознанно записывают ее решение.

2. Задачи с более сложными объектами для изображения представляются в виде условного рисунка.

Задача. В магазин привезли 3 коробки шоколадных конфет, а карамели на 2 коробки больше. Сколько коробок конфет привезли в магазин?

В выполнении модели краткой записи условия коробки изображают условно квадратами. Получается условная модель:

Ш. к. ???

К. ????? - ?

3. В процессе формирования опыта решения задач эту же составную задачу в целях сокращения выполнения модели условия можно представить в виде простейшей схемы:

Ш. к. _________3________

К. ____________________|______2______ - ?

В процессе ее анализа схема дополняется промежуточным вопросом (Сколько коробок карамели привезли в магазин?)

Ш. к. _________3________

К. ____________________|______2______ - ?

- ?

В данной схеме знаково-символически представлен план решения задачи. Его можно обозначить знаково на схеме:

Ш. к. _________3________

К. ____________________|______2______ - ? (2)

- ? (1)

В работе со схематическими моделями используются различные приемы усвоения этого вида знаково-символического моделирования условия задач. В качестве иллюстрации приведем пример.

Выбери схему для задачи:

    1. Во 2 классе 8 отличников, а в 3 классе 4. Во сколько раз во 2 классе отличников больше, чем в третьем? 2. В ателье за 1 день сшили 12 платьев, а костюмов в 3 раза меньше. Сколько костюмов сшили в ателье? 3. Купили 15 кг яблок, а винограда на 8 кг меньше. Сколько килограммов винограда купили? А) _______________________ б) ____________________

___________ ___________

В) ________________________ г) ____________

__________ _____________________

Решение задач на движение сопровождается моделями другого вида. Проиллюстрируем это примерами.

Задача. Из двух городов навстречу друг другу вышли два автомобиля. Скорость первого 80 км/ч, скорость второго 100 км/ч. Через сколько часов они встретятся, если расстояние между городами 540 км?

80 км/ч 100 км/ч

_________________________________________________________

540 км

4. Модели условий. Задач на пропорциональное деление чаще всего представляют в виде таблицы.

Задача. За 3 м ткани уплатили 540 руб. Сколько будут стоить 5 м такой же ткани?

Цена (руб.)

Количество (м)

Стоимость (руб.)

Одинаковая
    ? ?
    3 5
    540 ?

Знаково-символическая форма записи условия этой задачи позволяет определить план решения задачи.

Цена (руб.)

Количество (м)

Стоимость (руб.)

Одинаковая
    ? 1 ? 1
    3 5
    540 ? 2

Знаково-символическая модель условий задач на движение как одного из видов задач на пропорциональное деление может представляться и в виде таблицы.

Задача. Автомобиль, двигаясь со скоростью 75 км/ч, преодолевает некоторое расстояние за 4 ч. За сколько часов он преодолеет это расстояние, если его скорость увеличить на 25 км/ч?

Скорость (км/ч)

Время (ч)

Расстояние (км)

I

II
    75 -?, на 25 больше
    4 ?
    ? ?

Одинаковое

Эта модель условия содержит промежуточные вопросы, которые не только направляют ход анализа задачи, но и помогут обозначить план ее решения.

Скорость (км/ч)

Время (ч)

Расстояние (км)

I

II
    75 -? 2, на 25 больше
    4 ? 3
    ? 1 ? 1

Одинаковое

5. На более позднем этапе развития знаково-символических действий учащихся (по мере накопления опыта решения задач и формирования абстрактного мышления) практикуется словесный вид краткой записи условия задачи.

Задача. В первый день туристы проехали 120 км, во второй - на 40 км больше, в третий день - в 2 раза меньше, чем за первые два дня, а в четвертый - 1/7 пути, пройденного в третий день. Сколько километров туристы проехали за 3 дня?

I д. - 120 км

II д. - ? 1, на 40 км больше? 2 - ? 5

III д. - ? 3, в 2 раза меньше

IV д. - ? 4, 1/7 пути

Эта модель после анализа задачи поможет учащимся упорядочить процесс ее решения посредством присвоения промежуточным и главному вопросам порядка выполнения действий.

6. Менее применимой является знаково-символическая модель условия задачи в виде кругов Эйлера.

Задача. В группе туристов 18 чел. знали английский язык, 25 человек знали немецкий. Причем 8 чел. владели и английским, и немецким языками. 24 человека знали французский, причем 2 человека французов владели тремя языками, 4 человека французским и английским, 5 человек французским и немецким. Сколько было всего иностранных туристов в группе?

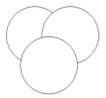
Этот тип задачи достаточно легко решается с применением именно такого вида краткой записи условия. Посредством логических рассуждений без опоры на знаково-символическую модель решение возможно лишь для незначительной части детей, у которых на достаточно высоком уровне для их возраста развито абстрактное мышление. Применение такого вида модели условия задачи возможно, та как учащиеся к периоду появления в учебнике таких задач владеют некоторыми элементарными основами теории множеств, выполняют операции объединения и пересечения множеств.

Мы показали процесс развития опыта представления условия текстовых задач посредством знаково-символических действий разного вида. Усвоение видов моделирования условий текстовых задач позволяет развивать мыслительные операции (анализ, синтез, сравнение, обобщение), характеризующие уровень развития математического мышления.

Похожие статьи




Методический аспект развития знаково-символических учебных действий - Схематическое моделирование условия задачи в развитии знаково-символических действий у младших школьников

Предыдущая | Следующая