Виды структуры оператора запаздывания во времени экзогенных переменных - Экономическое моделирование временных рядов
Модель Бокса и Дженкинса
Процедуры оценки параметров и прогнозирования, описанные в разделе Идентификация модели временных рядов, предполагают, что математическая модель процесса известна. В реальных данных часто нет отчетливо выраженных регулярных составляющих. Отдельные наблюдения содержат значительную ошибку, тогда как вы хотите не только выделить регулярные компоненты, но также построить прогноз. Методология АРПСС, разработанная Боксом и Дженкинсом (1976), позволяет это сделать. Данный метод чрезвычайно популярен во многих приложениях, и практика подтвердила его мощность и гибкость (Hoff, 1983; Pankratz, 1983; Vandaele, 1983). Однако из-за мощности и гибкости, АРПСС - сложный метод. Его не так просто использовать, и требуется большая практика, чтобы овладеть им. Хотя часто он дает удовлетворительные результаты, они зависят от квалификации пользователя (Bails and Peppers, 1982). Следующие разделы познакомят вас с его основными идеями. Для интересующихся кратким, рассчитанным на применение, (нематематическим) введением в АРПСС, рекомендуем книгу McCleary, Meidinger, and Hay (1980). [2, с. 236]
Процесс авторегрессии. Большинство временных рядов содержат элементы, которые последовательно зависят друг от друга. Такую зависимость можно выразить следующим уравнением:
Xt = + 1*x(t-1) + 2*x(t-2) + 3*x(t-3) + ... +
Здесь:
- константа (свободный член),
1, 2, 3 - параметры авторегрессии.
Вы видите, что каждое наблюдение есть сумма случайной компоненты (случайное воздействие, ) и линейной комбинации предыдущих наблюдений.
Требование стационарности. Заметим, что процесс авторегрессии будет стационарным только, если его параметры лежат в определенном диапазоне. Например, если имеется только один параметр, то он должен находиться в интервале -1<<+1. В противном случае, предыдущие значения будут накапливаться и значения последующих xt могут быть неограниченными, следовательно, ряд не будет стационарным. Если имеется несколько параметров авторегрессии, то можно определить аналогичные условия, обеспечивающие стационарность (см. например, Бокс и Дженкинс, 1976; Montgomery, 1990).
Процесс скользящего среднего. В отличие от процесса авторегрессии, в процессе скользящего среднего каждый элемент ряда подвержен суммарному воздействию предыдущих ошибок. В общем виде это можно записать следующим образом:
Xt = µ + t - 1*(t-1) - 2*(t-2) - 3*(t-3) - ...
Здесь:
µ - константа,
1, 2, 3 - параметры скользящего среднего.
Другими словами, текущее наблюдение ряда представляет собой сумму случайной компоненты (случайное воздействие, ) в данный момент и линейной комбинации случайных воздействий в предыдущие моменты времени.
Обратимость. Не вдаваясь в детали, отметим, что существует "двойственность" между процессами скользящего среднего и авторегрессии (см. например, Бокс и Дженкинс, 1976; Montgomery, Johnson, and Gardiner, 1990). Это означает, что приведенное выше уравнение скользящего среднего можно переписать (обратить) в виде уравнения авторегрессии (неограниченного порядка), и наоборот. Это так называемое свойство обратимости. Имеются условия, аналогичные приведенным выше условиям стационарности, обеспечивающие обратимость модели.
Распределенный лаг Алмона
Обычная проблема, возникающая в множественной регрессии, состоит в том, что соседние значения x сильно коррелируют. В самом крайнем случае, это приводит к тому, что корреляционная матрица не будет обратимой и коэффициенты бета не могут быть вычислены. В менее экстремальных ситуациях вычисления этих коэффициентов и их стандартные ошибки становятся ненадежными из-за вычислительных ошибок (ошибок округления). В контексте множественной регрессии эта проблема хорошо известна как проблема мультиколлинеарность.
Алмон (1965) предложил специальную процедуру, которая в данном случае уменьшает мультиколлинеарность. Именно, пусть каждый неизвестный коэффициент записан в виде:
I = 0 + 1*i + ... + q*iq
Алмон показал, что во многих случаях (в частности, чтобы избежать мультиколлинеарности) легче оценить коэффициенты альфа, чем непосредственно коэффициенты бета. Такой метод оценивания коэффициентов бета называется полиномиальной аппроксимацией.
Неправильная спецификация. Общая проблема полиномиальной аппроксимации, состоит в том, что длина лага и степень полинома неизвестны заранее. Последствия неправильного определения (спецификации) этих параметров потенциально серьезны (в силу смещения, возникающего в оценках при неправильном задании параметров).
Пример. Имеются следующие данные (х -- доход, ден. ед., y -- расход на потребление некоторого блага; табл. 1).
Таблица 1
|
Условное время |
X |
Y |
Z0 |
Z1 |
Z2 |
|
1 |
11,4 |
13,2 |
- |
- |
- |
|
2 |
11,8 |
14 |
- |
- |
- |
|
3 |
7,1 |
12,5 |
- |
- |
- |
|
4 |
10,4 |
13 |
40,7 |
64,9 |
156,9 |
|
5 |
7,5 |
11,5 |
36,8 |
60 |
145 |
|
6 |
14 |
13,8 |
39 |
49,6 |
113 |
|
7 |
9,9 |
13,8 |
41,8 |
60,2 |
137,6 |
|
8 |
14,4 |
15,9 |
45,8 |
60,4 |
133,4 |
|
9 |
9 |
14 |
47,3 |
76,2 |
180 |
|
10 |
9,4 |
13,3 |
42,7 |
67,5 |
155,7 |
|
11 |
14,9 |
15,7 |
47,7 |
70,6 |
175 |
|
12 |
15,3 |
16,9 |
48,6 |
60,7 |
133,5 |
|
13 |
12,8 |
16,5 |
52,4 |
73,3 |
159,5 |
|
14 |
14,8 |
17,6 |
57,8 |
88,1 |
208,1 |
|
15 |
9,6 |
15,3 |
52,5 |
86,3 |
203,7 |
|
16 |
18 |
18,1 |
55,2 |
77,6 |
184 |
|
17 |
11,3 |
16,8 |
53,7 |
81,6 |
189,6 |
|
18 |
9,8 |
14,8 |
48,7 |
76,1 |
169,7 |
Пусть число лагов равно трем и веса в модели Алмон подчиняются полиному второй степени, т. е.
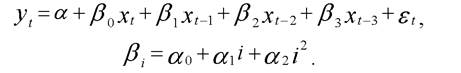
Тогда модель примет вид:
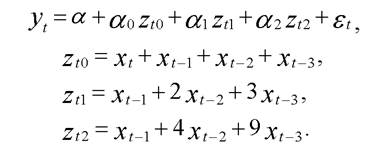
После оценки параметров получим эмпирическое уравнение регрессии:
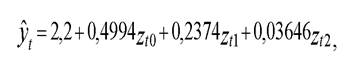
Следовательно
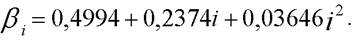
Возвращаясь к исходным переменным, получим:
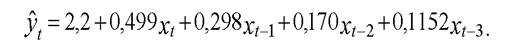
Нелинейный метод наименьших квадратов. Метод Койка
В случае если модель с распределенным лагом характеризуется бесконечной величиной максимального лага L, то для оценивания неизвестных параметров данной модели применяются нелинейный метод наименьших квадратов и метод Койка. При ???м исходят из предположения о геометрической структуре лага, т. е. влияние лаговых значений факторной переменной на результативную переменную уменьшается с увеличением величины лага в геометрической прогрессии.
В случае если в модель включена только одна объясняющая переменная, то ее можно представить в виде:
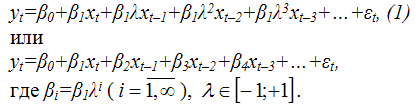
В модели с распределенным лагом (1) неизвестными будут три параметра: в0, в1 и л. Найти оценки данных параметров с помощью традиционного метода наименьших квадратов невозможно по нескольким причинам, по???му в данном случае могут быть использованы нелинейный метод наименьших квадратов и метод Койка
Суть нелинейного метода наименьших квадратов состоит по сути в том, что для параметра
Л определяются значения в интервале [-1;+1] с определенным шагом, например, 0,05 (чем меньше шаг, тем точнее будет результат).
Несмотря на то, что метод Койка очень удобен в вычислительном отношении (оценки параметровв0, в1 и л можно рассчитать с помощью традиционного метода наименьших квадратов), оценки, полученные с его помощью, будут смещенными и несостоятельными, т. к. нарушается первое условие нормальной линейной модели регрессии.
Похожие статьи
-
Примеры лаговых моделей в экономике - Экономическое моделирование временных рядов
Модель адаптивных ожиданий Моделью адаптивных ожиданий называется динамическая эконометрическая модель, которая учитывает предполагаемое (или желаемое)...
-
Лаговые модели - Экономическое моделирование временных рядов
Для многих экономических процессов характерно, что эффект от воздействия некоторого фактора на показатель, характеризующий процесс, оказывается не сразу,...
-
Аналитическое выравнивание временного ряда. - Моделирование в эконометрике
Рассмотрим модель временного ряда yT = F (t) + , где F (t) - неслучайная составляющая (тренд, либо тренд и циклическая и (или) сезонная компонента,...
-
Введение - Моделирование времени жизни ипотечного кредита
Постановка задачи. Экономическое и практическое обоснование важности ее решения. Рассмотрим задачу моделирования денежных потоков по портфелю (пулу)...
-
По данным динамики валют (вариант 14) выявить трендовую, периодическую и случайную составляющие ряда (T, S,E), оценить качество модели, сделать прогноз...
-
Экономико-математические методы представляют собой совокупность математических методов (математического программирования, теории вероятностей, теории...
-
Множественная регрессия - уравнение связи с несколькими независимыми переменными: где - зависимая переменная (результативный признак); - независимые...
-
1. Определение параметров модели парной линейной регрессии методом наименьших квадратов 2. Оценка тесноты связи между переменными 3. Оценка качества...
-
Моделирование временной переменная автокорреляция Главным инструментом эконометрического исследования является модель. Выделяют три основных класса...
-
Результат функционирования имитационной модели во многом зависит от внутренних управляемых параметров. Поэтому, представляет интерес рассмотрение влияние...
-
Данная программа представляет собой реализацию имитации реального объекта, то есть документооборота отдела с помощью имитационной модели. Поскольку...
-
Описание реальных отношений между экономическими объектами и производственными процессами наиболее рационально и в полной мере осуществляется с помощью...
-
После получения матриц спектра плана, проведем 70 опытов в каждой точке. По полученным параметрам построим регрессионную модель второго порядка,...
-
Приведем данные среднегодовой численности занятого населения Год Тыс. чел. 1996 2301,3 1997 2341,4 1998 2329,8 1999 2351,6 2000 2367,8 2001 2372,3 2002...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
В состав системы эконометрических уравнений входят множество зависимых или эндогенных переменных и множество предопределенных переменных (лаговые и...
-
Суть, причины и последствия автокорреляции. - Моделирование в эконометрике
Одной из предпосылок регрессионного анализа является независимость случайного члена в любом наблюдении от его значений во всех других наблюдениях, т. е....
-
Неслучайная составляющая временного ряда и методы его сглаживания - Динамические ряды
Существенную роль в решении задач выявления и оценивания трендовой, сезонной и циклической составляющих в разложении (1.1.1) играет начальный этап...
-
1. Предпосылки метода наименьших квадратов. 2. Проблема мультиколлинеарности. 3. Гомоскедатичность и гетероскедатичность. Линейные регрессионные модели с...
-
Простая линейная регрессия - Моделирование в эконометрике
Простой регрессией называется односторонняя стохастическая зависимость результативной переменной только от одной объясняющей переменной: Простая линейная...
-
Постоянство механизмов. Одно из условий, на которое опирается эконометрическое моделирование, состоит в том, что функциональное соотношение не меняется в...
-
Основные этапы построения эконометрической модели - Моделирование в эконометрике
Построение эконометрической модели является основой эконометрического исследования. Оно основывается на предположении о реально существующей зависимости...
-
Выбор математической формы функции при моделировании зависимости выпуска продукции от производственных факторов Постановка проблемы. Одним из важнейших...
-
Прогнозирование в регрессионных моделях - Эконометрика как наука
Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области научных знаний: техническое...
-
Авторегрессионные модели со скользящими средними в остатках (ARMA(p, q)-модели) - Динамические ряды
Представление процесса типа МА в виде процесса авторегрессии неэкономично с точки зрения его параметризации. Аналогично процесс AR не может быть...
-
Коэффициент детерминации - Математическое описание связи: регрессия, корреляция
Предположим, что экономические предпосылки и анализ расположения точек на корреляционном поле позволил нам выдвинуть гипотезу о том, что зависимость...
-
Критерии диагностики автокорреляции в лаговых моделях - Экономическое моделирование временных рядов
Критерий Дарбина-Уотсона применяют для обнаружения автокорреляции, подчиняющейся авторегрессионному процессу 1-го порядка. Предполагается, что величина...
-
Понятие и структура экономической системы. - Моделирование экономических систем
Употребление понятия системы имеет долгую историю, уходящую в античную эпоху. В переводе с греческого "система" означает некое целое, состоящее из...
-
При анализе инновационной активности региона важно понимать, как те или иные экономические данные влияют на инновационные показатели. В качестве...
-
Модель временного ряда на примере продажи акций - Эконометрическое моделирование финансовых рынков
Рассмотрим пример на основе данных по ценам продажи акций. Даны цены (открытия, максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания...
-
Основные задачи анализа временных рядов. Базисная цель статистического анализа временного ряда заключается в том, чтобы по имеющейся траектории этого...
-
Временные ряды - Эконометрическое моделирование финансовых рынков
При построении эконометрической модели используются два типа данных: 1) данные, характеризующие совокупность различных объектов в определенный момент...
-
Уравнение динамики теплообменника: Передаточные функции объекта получим по его уравнению динамики. Для этого запишем уравнение по заданному каналу. Затем...
-
В результате выполнения курсовой работы были достигнуты следующие результаты: - изучены методы построения имитационных моделей реальных экономических...
-
Временные ряды - Моделирование в эконометрике
Эконометрический модель регрессия ряд Понятие временного ряда. Основные характеристики временных рядов. Модели стационарных и нестационарных временных...
-
Проблема прогнозирования вероятности банкротства существует уже несколько десятков лет - все началось с работ Ramser, Foster (1931), Fitzpatrick (1932) и...
-
Фиктивные переменные во множественной регрессии - Моделирование в эконометрике
До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может...
-
Особенности экономических наблюдений и измерений. - Моделирование перспективного развития экономики
Уже длительное время главным тормозом практического при-менения математического моделирования в экономике является на-полнение разработанных моделей...
-
Оптимизационная модель экономической коррупции имеет вид (1) Где b - величина взятки, r(b) - функция экономической коррупции (например, фактическое...
-
Модели стационарных временных рядов и их идентификация - Динамические ряды
В 2.2 рассматривался класс стационарных временных рядов, в рамках которого подбирается модель, пригодная для описания поведения случайных остатков...
Виды структуры оператора запаздывания во времени экзогенных переменных - Экономическое моделирование временных рядов