Оптимальный план - Модели оптимального плана управления запасами
Найдем наилучший план поставок. План, для которого в моменты доставок очередных партий запас равен 0 (т. е. y(t) = 0), назовем напряженным.
Утверждение 1. Для любого плана поставок, не являющегося напряженным, можно указать напряженный план, для которого средние издержки меньше.
Покажем, как можно от произвольного плана перейти к напряженному плану, уменьшив при этом издержки. Пусть с течением времени при приближении к моменту t1 прихода поставки Q1 уровень запаса не стремится к 0, а лишь уменьшается до положительного значения y(t1-) (где знак "минус" означает предел слева функции y(t) в точке t1). Тогда рассмотрим новый план поставок с теми же моментами поставок и их величинами, за исключением величин поставок в моменты t = 0 и t = t1. А именно, заменим Q0 на Q01 = Q0 - y(t1-), а Q1 на Q11 = Q0 + y(t1-). Тогда график уровня запаса на складе параллельно сдвинется вниз на интервале (0; t1), достигнув 0 в t1, и не изменится правее точки t1. Следовательно, издержки по доставке партий не изменятся, а издержки по хранению уменьшатся на величину, пропорциональную (с коэффициентом пропорциональности s) площади параллелограмма, образованного прежним и новым положениями графика уровня запаса на интервале (0; t1) (см. рис.2).
Итак, в результате первого шага перехода получен план, в котором крайний слева зубец достигает оси абсцисс. Следующий шаг проводится аналогично, только момент времени t = 0 заменяется на t = t1. Если есть такая возможность, второе наклонное звено графика уровня запаса на складе параллельно сдвигается вниз, достигая в крайней правой точке t2 оси абсцисс.
Аналогично поступаем со всеми остальными зубцами, двигаясь слева направо. В результате получаем напряженный план. На каждом шагу издержки по хранению либо сокращались, либо оставались прежними (если соответствующее звено графика не опускалось вниз). Следовательно, для полученного в результате описанного преобразования напряженного плана издержки по хранению меньше, чем для исходного плана, либо равны (если исходный план уже являлся напряженным).
Из утверждения 1 следует, что оптимальный план следует искать только среди напряженных планов. Другими словами, план, не являющийся напряженным, не может быть оптимальным.
Утверждение 2. Среди напряженных планов с фиксированным числом поставок минимальные издержки имеет тот, в котором все интервалы между поставками равны.
При фиксированном числе поставок затраты на доставку партий не меняются. Следовательно, достаточно минимизировать затраты на хранение.
Для напряженных планов размеры поставок однозначно определяются с помощью интервалов между поставками:
Действительно, очередная поставка величиной Qi-1 совпадает с размером запаса на складе в момент ti-1, расходуется с интенсивностью м единиц товара в одну единицу времени и полностью исчерпывается к моменту ti прихода следующей поставки.
Для напряженного плана издержки по хранению равны
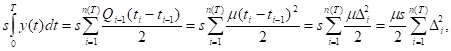
Где Дi = ti - ti-1, i = 1, 2,..., n(T), tn(T) = T. Ясно, что Дi, i = 1, 2,..., n(T), - произвольные неотрицательные числа, в сумме составляющие Т. Следовательно, для минимизации издержек среди напряженных планов с фиксированным числом поставок достаточно решить задачу оптимизации
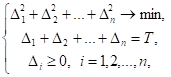
Где n = n(T).
Полученная задача оптимизации формально никак не связана с логистикой, она является чисто математической. Для ее решения целесообразно ввести новые переменные бi = Дi - T/n, i = 1, 2,..., n. Тогда
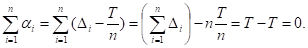
Поскольку Дi = T/n + бi, то
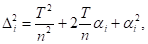
Следовательно, с учетом предыдущего равенства имеем
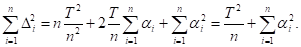
Сумма квадратов всегда неотрицательна. Она достигает минимума, равного 0, когда все переменные равны 0, т. е. при б1 = б2 =... = бn = 0. Тогда
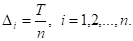
При этих значениях Дi выполнены все ограничения оптимизационной задачи. Итак, утверждение 2 доказано.
Для плана с равными интервалами между поставками все партии товара имеют одинаковый объем. Для такого плана издержки по хранению равны
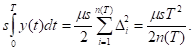
Средние издержки (на единицу времени) таковы:
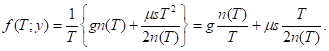
Итак, минимизация средних издержек - это задача дискретной оптимизации. На третьем этапе построения оптимального плана необходимо найти натуральное число n(T) - самое выгодное число поставок.
Поскольку к моменту Т запас товара должен быть израсходован, то общий объем поставок за время T должен совпадать с общим объемом спроса, следовательно, равняться мТ. Справедливо балансовое соотношение (аналог закона Ломоносова-Лавуазье сохранения массы при химических реакциях):
Из балансового соотношения следует, что
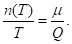
Средние издержки (на единицу времени) можно выразить как функцию размера партии Q:
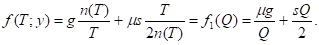
(1)
Задача состоит в минимизации f1(Q) по Q. При этом возможная величина поставки принимает дискретные значения, поскольку
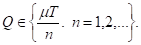
Изучим функцию f1(Q), определенную при Q > 0. При приближении к 0 она ведет себя как гипербола, при росте аргумента - как линейная функция. Производная имеет вид
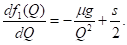
(2)
Производная монотонно возрастает, поэтому рассматриваемая функция имеет единственный минимум в точке, в которой производная равна 0, т. е. при
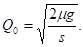
(3)
Получена знаменитая в теории управления запасами "формула квадратного корня".
В литературе иногда без всяких комментариев рекомендуют использовать напряженный план, в котором размеры всех поставляемых партий равны Q0. К сожалению, получаемый таким путем план почти всегда не является оптимальным, т. е. популярная рекомендация неверна или не вполне корректна. Дело в том, что почти всегда
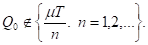
Как же найти оптимальный план? Всегда можно указать неотрицательное целое число n такое, что
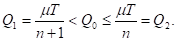
(4)
Утверждение 3. Решением задачи оптимизации
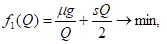
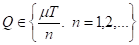
Является либо Q1, либо Q2.
Действительно, из всех возможных объемов партии
Часть лежит правее Q0, из них наименьшим является Q2, а часть лежит левее Q0, из них наибольшим является Q1. Для построения оптимального плана обратим внимание на то, что производная (2) отрицательна левее Q0 и положительна правее Q0, следовательно, функция средних издержек f1(Q) убывает левее Q0 и возрастает правее Q0. Значит, минимум по
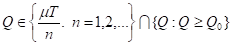
Достигается при Q = Q2, а минимум по
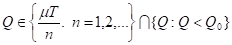
- при Q = Q1 Последнее утверждение эквивалентно заключению утверждения 3.
Итак, алгоритм построения оптимального плана таков.
- 1. Найти Q0 по формуле квадратного корня (3). 2. Найти n из условия (4). 3. Рассчитать f1(Q) по формуле (1) для Q = Q1 и Q = Q2, где Q1 и Q2 определены соотношением (4). 4. Наименьшее из двух чисел f1(Q1) и f1(Q2) является искомым минимумом, а то из Q1 и Q2, на котором достигается минимум - решением задачи оптимизации. Обозначим его Qopt.
Итак, оптимальный план поставки - это напряженный план, в котором объемы всех поставок равны Qopt.
Замечание. Если f1(Q1) = f1(Q2), то решение задачи оптимизации состоит из двух точек Q1 и Q2. В этом частном случае существует два оптимальных плана.
Пример 1. На складе хранится некоторая продукция, пользующаяся равномерным спросом. За 1 день со склада извлекается 5 т продукции. Плата за хранение 1 т. продукции в день - 50 руб. Плата на доставку одной партии - 980 руб. Горизонт планирования - 10 дней. Найти оптимальный план поставок.
В рассматриваемом случае м = 5 (т/день), s = 50 (руб./т. день), g = 980 (руб./партия), Т = 10 (дней). По формуле (3) рассчитываем
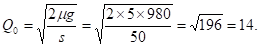
Множество допустимых значений для Q имеет вид
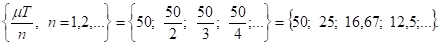
Следовательно, Q1 = 12,5 и Q2 = 16,67. Первое значение определяет напряженный план с четырьмя одинаковыми зубцами, а второе - с тремя. Поскольку
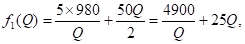
То
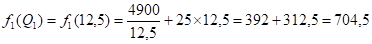
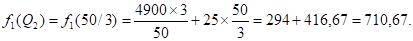
Поскольку f1(Q1) < f1(Q2), то Qopt = Q1 = 12,5. Итак, оптимальным является напряженный план с четырьмя зубцами.
Как уже отмечалось, часто рекомендуют применять план поставок с Q=Q0. Каков при этом проигрыш по сравнению с оптимальным планом?
Для плана с Q=Q0 интервал между поставками составляет Q0/м = 14/5 = 2,8 дня. Следовательно, партии придут в моменты t0 = 0; t1= 2,8; t2 = 5,6; t3 = 8,4. Следующая партия должна была бы придти уже за пределами горизонта планирования Т =10, в момент t4 = 11,2. Таким образом, график уровня запаса на складе в пределах горизонта планирования состоит из трех полных зубцов и одного не полного. К моменту Т =10 пройдет 10 - 8,4 = 1,6 дня с момента последней поставки, значит, со склада будет извлечено 5Ч1,6 = 8 т продукции и останется 14 - 8 = 6 т. План с Q=Q0 не является напряженным, а потому не является оптимальным для горизонта планирования Т =10.
Подсчитаем общие издержки в плане с Q=Q0. Площадь под графиком уровня запаса на складе равна сумме площадей трех треугольников и трапеции. Площадь треугольника равна (14Ч2,8)/2 = 19,6, трех треугольников - 58,8. Основания трапеции параллельны оси ординат и равны значениям уровня запаса в моменты времени t3 = 8,4 и Т =10, т. е. величинам 14 и 6 соответственно. Высота трапеции лежит на оси абсцисс и равна 10 - 8,4 = 1,6, а потому площадь трапеции есть [(14+6)Ч1,6]/2 = 16. Следовательно, площадь под графиком равна 58,8 + 16 = 74,8, а плата за хранение составляет 50Ч74,8 = 3740 руб.
За 10 дней доставлены 4 партии товара (в моменты t0 = 0; t1= 2,8; t2 = 5,6; t3 = 8,4). Следовательно, затраты на доставку равны 4Ч980 = 3920 руб. Общие издержки за 10 дней составляют 3740 + 3920 = 7660 руб., а средние издержки - 766 руб. Они больше средних издержек в оптимальном плане в 766/704,5 = 1,087 раза, т. е. на 8,7%.
Отметим, что
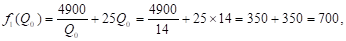
Т. е. меньше, чем в оптимальном плане. Таким образом, из-за дискретности множества допустимых значений средние издержки возросли на 4,5 руб., т. e. на 0,64%.
При этом оптимальный размер партии (12,5 т) отличается от Q0 = 14 т на 1,5 т, т. е. Qopt/Q0 = 0,89 - различие на 11%. Достаточно большое различие объемов поставок привело к пренебрежимо малому изменению функции f1(Q). Это объясняется тем, что в точке Q0 функция f1(Q) достигает минимума, а потому ее производная в этой точке равна 0.
Оба слагаемых в f1(Q0) равны между собой. Случайно ли это? Покажем, что нет. Действительно,
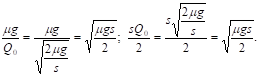
Таким образом, составляющие средних издержек, порожденные различными причинами, уравниваются между собой.
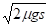
Средние издержки в плане с Q=Q0 равны. Интервал между поставками при этом равен
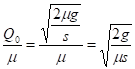
.
Издержки в течение одного интервала между поставками таковы:
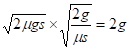
,
При этом половина (т. е. g) приходится на оплату доставки партии, а половина - на хранение товара.
Итак, план Вильсона хуже оптимального плана. Однако оказывается, что при росте интервала планирования отношение средних издержек в этих двух планах приближается к 1.
Похожие статьи
-
Асимптотически оптимальный план - Модели оптимального плана управления запасами
Из проведенных рассуждений ясно, что напряженный план с Q=Q0 является оптимальным тогда и только тогда, когда горизонт планирования Т приходится на...
-
Классическая модель управления запасами - Модели оптимального плана управления запасами
Пусть y(t) - величина запаса некоторого товара на складе в момент времени t, t>0. Дефицит не допускается, т. е. y(t)>0 при всех t. Товар пользуется...
-
Детерминированные модели, Модель Уилсона - Экономико-математические модели управления запасами
Чрезвычайно трудно построить обобщенную модель управления запасами, которая учитывала бы все разновидности условий, наблюдаемых в реальных системах. Но...
-
Модель с определением точки заказа - Экономико-математические модели управления запасами
В реальных ситуациях следует учитывать время выполнения заказа Q. Для обеспечения бесперебойного снабжения заказ должен подаваться в момент, когда...
-
Введение - Экономико-математические модели управления запасами
Разница в ритме производства продукции у различных поставщиков, дискретность процесса поставок, возможность случайных колебаний в интенсивности...
-
Влияние отклонений от оптимального объема партии - Модели оптимального плана управления запасами
В реальных производственных и управленческих ситуациях часто приходится принимать решения об использовании объемов партии, отличных от оптимальной...
-
Модель с учетом неудовлетворенных требований - Экономико-математические модели управления запасами
В некоторых случаях, когда потери из-за дефицита сравнимы с издержками хранения, дефицит допускается. Пусть требования, поступающие в момент отсутствия...
-
Вопросы практического применения классической модели управления запасами рассмотрены в [20, 26]. Для отработки методики практического использования этой...
-
Модели теории игр. Основные определения и термины В разных областях целенаправленной деятельности, например при разработке и эксплуатации АСУ, часто...
-
Пусть заказанная партия поступает с интенсивностью u единиц в единицу времени. Очевидно система может работать без дефицита, если интенсивность поставок...
-
Программное управление Относительно просто может быть сформулирована так называемая задача программного управления. В ней предполагается, что управляющие...
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
В зависимости от содержания задачи может быть два случая: когда ребра графа G единичной длины; когда ребра графа произвольной длины. Для каждого из этих...
-
Постановка задачи применительно для КУП "СПЕЦКОММУНТРАНС": двум погрузчикам разной мощности, это автомобили ТО 28 и ТО 49, за 23 часа нужно погрузить на...
-
Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....
-
Введение - Модели оптимального плана управления запасами
Экономико-математической теории управления запасами в 2015 г. исполняется 100 лет (отсчитывая с работы Ф. Харриса [1]). Она входит в логистику - одну из...
-
Модель с фиксированной периодичностью предполагает, что размеры заказов различны для разных циклов. Таким образом, размер запаса регулируется за счет...
-
Заключение - Экономико-математические модели управления запасами
В любой задаче управления запасами решается вопросы выбора размеров и сроков размещения заказов на запасаемую продукцию. К сожалению, общее решение этой...
-
Теория игр исследует оптимальные стратегии в ситуациях игрового характера. К ним относятся ситуации, связанные с выбором наивыгоднейших производственных...
-
Из перечисленного обзора типов ММ, составляющих предмет ИСО, можно выделить следующие особенности ММ ИСО [3]. - Системный подход, заставляющий...
-
Наиболее ранним способом формализации экономико-математических и ТС является представление физических явлений с помощью систем дифференциальных...
-
Комментарии к третьему разделу курсовой работы В третьем разделе курсовой работы студенту предлагается определить оптимальную стратегию заказа в условиях...
-
В качестве примера конкретной модели процесса управления обсудим модель распределения времени между овладением знаниями и развитием умений, впервые...
-
При использовании такой стратегии уровень запаса отслеживается непрерывно. Опасность исчерпания запаса возникает здесь только в течение времени...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Вероятностные модели управления запасами - Экономико-математические модели управления запасами
Резервный запас - это величина запаса, постоянно поддерживаемая дополнительно к ожидаемой потребности. В случае нормального распределения колебаний...
-
Оптимальное управление запасами - выбор таких объемов и моментов поставок, когда суммарные издержки системы снабжения будут минимальными. Простейшие...
-
Сравнительный анализ формул, полученных для числа циклов и исходных объемов финансового и материального потоков технологической цепи хлебопродуктового...
-
В реальных производственных условиях, во-первых, не может быть мгновенных поставок партий исходного продукта переработки, а во-вторых, технологический...
-
Основные понятия линейного программирования - Оптимальное программирование
Математические исследования отдельных экономических проблем, математическая формализация числового материала проводилась еще в XIX веке. При...
-
При управлении подвижными объектами (такими, например, как мобильные роботы, подводные аппараты и т. п.) часто имеет место неопределенность цели, когда...
-
Важным этапом изучения явлений предметов процессов является их классификация, выступающая как система соподчиненных классов объектов, используемая как...
-
Экономико-математические модели управления запасами
> Таблица Брауна Показывает зависимость ожидаемого дефицита изделий (E(z)) от резервного запаса, выраженного в стандартных отклонениях спроса (z)....
-
Формирование цен различных товаров зависит от большого числа факторов, совокупное влияние которых не может быть детерминировано в рамках общей модели без...
-
Модели линейного программирования. Основные определения Еще одним классом задач экономико-математического моделирования являются задачи линейного...
-
В соответствии с принципиальной схемой технологического процесса и в целях четкой организации работ рекомендуется составлять технологические карты,...
-
Введение - Место и значение управления запасами в логистике производственного предприятия
Термин "логистика", известный до недавнего времени лишь узкому кругу специалистов, получает сегодня широкое распространение. Основная причина этого...
-
Основные понятия и обозначения Динамическое программирование как самостоятельная дисциплина сформировалась в пятидесятых годах двадцатого века. Большой...
-
Уровень науки и техники Надежность средств, с помощью которых человек достигает космоса высокая, но не идеальна. РН -- сложная конструкция, и даже в...
-
Экономические задачи, сводящиеся к транспортной модели Транспортная модель используется для составления наиболее экономичного плана перевозок одного вида...
Оптимальный план - Модели оптимального плана управления запасами