Об инфинитезимальных изометриях продолженных почти контактных метрических структур
Об инфинитезимальных изометриях продолженных почти контактных метрических структур
На распределении почти контактной метрической структуры строится продолженная почти контактная метрическая структура. Доказывается, что полный лифт инфинитезимальной изометрии исходной структуры является инфинитезимальной изометрией продолженной структуры.
Пусть Х - гладкое многообразие нечетной размерности N=2m+1, - - модуль гладких векторных полей на Х. Все многообразия, тензорные поля и другие геометрические объекты предполагаются гладкими класса. В работах [1-6] изучались (продолженные) почти контактные метрической структуры, естественным образом определяемые на распределенииD почти контактной метрической структуры.
В предлагаемой работе используются так называемые адаптированные координаты [3]. Карту (Б, В, Г = 1,..., N; a, B, C, E = 1,..., N-1) многообразия X будем называть адаптированной к неголономному многообразию D, если. Пусть P: TX>D - проектор, определяемый разложением. Векторные поля линейно независимы и в области определения соответствующей карты порождают систему D: . Таким образом, мы имеем на многообразии X неголономное поле базисов и соответствующее ему поле кобазисов. Адаптированным будем называть также базис, как базис, определяемый адаптированной картой. Тензорное поле типа (P, q), заданное на почти контактном метрическом многообразии, назовем допустимым (к распределению D), если его координатное представление в адаптированной карте имеет вид:
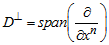
.
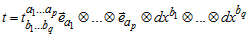
Введем на D структуру гладкого многообразия, поставив в соответствие каждой адаптированной карте на многообразии X сверхкарту на многообразии D, где XN+a - координаты допустимого вектора в базисе. Построенную сверхкарту также будем называть адаптированной. Пусть на многообразии X задана контактная метрическая структура. Определим на распределении D как на гладком многообразии почти контактную метрическую структуру, полагая, , , , .
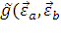
Векторные поля определяются здесь продолженной связностью [1-6]. Полученную структуру будем называть продолженной почти контактной метрической структурой.
Теорема. Пусть - допустимое векторное поле Киллинга, заданное на многообразии X. Тогда, полный лифт поля : , является инфинитезимальной изометрией.
Доказательство теоремы сводится к непосредственным вычислением производной Ли от метрического тензора, координатное представление которого имеет вид
.
Библиографический список
- 1. Букушева А. В., Галаев С. В. Почти контактные метрические структуры, определяемые связностью над распределением с допустимой финслеровой метрикой // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2012. Т.12. Вып.3. С.17-22. 2. Букушева А. В., Галаев С. В. Связности над распределением и геодезические пульверизации // Известия вузов. Математика. 2013. №4. С.1-9. 3. Галаев С. В. Внутренняя геометрия метрических почти контактных многообразий // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2012. Т.12. Вып.1. С.16-22. 4. Галаев С. В. Почти контактные кэлеровы многообразия постоянной голоморфной секционной кривизны // Известия вузов. Математика. 2014. №8. С.42-52. 5. Букушева А. В. О геометрии слоений на распределениях с финслеровой метрикой // Известия Пензенского государственного педагогического университета имени В. Г. Белинского. (Серия физико-математические и технические науки). 2012. №30. С.33-38. 6. Букушева А. В. Слоения на распределениях с финслеровой метрикой // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2014. Т.14. Вып.3. С.247-251.
Похожие статьи
-
СПОСОБЫ ОПИСАНИЯ СТРУКТУР. МОРФОЛОГИЯ СОЦИАЛЬНО-ПОЛИТИЧЕСКОЙ И ЭКОНОМИЧЕСКОЙ СФЕР Структурное моделирование. Структурный анализ Основная цель...
-
ПОДГОТОВКА ОБЖИГОВОГО ГАЗА К КОНТАКТНОМУ ОКИСЛЕНИЮ. - Получение серной кислоты
Подготовка обжигового газа к контактному окислению заключается в удалении из него примесей, присутствие которых может вызвать затруднения при проведении...
-
КОНТАКТНЫЙ МЕТОД ПОЛУЧЕНИЯ СЕРНОЙ КИСЛОТЫ. - Получение серной кислоты
Рассмотрим процесс получения серной кислоты контактным методом из двух видов сырья: серного (железного) колчедана и серы. Получение H2SO4 из колчедана....
-
Многообразия - Формационные основы универсальных алгебр
8.1. Пусть и -- слова сигнатуры в счетном алфавите. Тогда формальное равенство называется - тождеством или тождеством сигнатуры. Пусть тождество имеет...
-
Понятие и структура экономической системы. - Моделирование экономических систем
Употребление понятия системы имеет долгую историю, уходящую в античную эпоху. В переводе с греческого "система" означает некое целое, состоящее из...
-
Реализация интеллектуальных систем поддержки решений (ИСППР) в задачах оценки перспективности объектов природопользования на ранних стадиях их...
-
В основе модели крупномасштабной транспортной сети лежит принцип иерархической организации территорий (в нисходящем направлении). Рассмотрим карту сети...
-
Понятие, классификация и структура инвестиций Инвестиции (от лат. investire -- облачать) -- вложение капитала в объекты предпринимательской и иной...
-
Статистические испытания схемы проводятся исходя из того, что генерирование случайных логических переменных xI проводится с помощью равномерного...
-
СТРУКТУРЫ УПРАВЛЕНИЯ ЛОГИСТИЧЕСКИМИ СИСТЕМАМИ - Понятие и виды логистической системы
Объектом логистическими системами, как известно является сквозной материальный поток, тем не менее на отдельных участках управление им имеет известную...
-
Моделирование (в широком смысле) является основным методом исследований во всех областях знаний и научно обоснованным методом оценок характеристик...
-
Контактный способ - Сера и ее соединения
При производстве серной кислоты применяют различное сырье. Чистая сера стала применяться в ГДР только недавно. В большинстве случаев на предприятиях...
-
Структура генома, Клеточная структура и метаболизм - Этапы получения лизина
Corynebacterium glutamicum имеет при себе круговую хромосому и несколько плазмид. Ее геном состоит из 3314179 нуклеотидов (в расчет берется геном штамма...
-
Решетки (структуры) - Формационные основы универсальных алгебр
Понятие решетки (пример 11) играет исключительно важную роль в изучении самых общих алгебр. И это, в первую очередь, связано с иным подходом в...
-
Цель организационной структуры состоит в том, чтобы обеспечить достижение стоящих перед организацией задач. Согласно классической теории организации, с...
-
Формирование требований к информационной системе Организационная структура предприятия Организационная структура ВУЗа представлена на рисунке 1.1. Рис...
-
Восприятие и описание структур - Системная революция и принцип дуального управления
На рис. 2.1.3 представлена общая схема взаимосвязи различных уровней восприятия Наблюдателем структуры реальных систем. Процесс восприятия некоторой...
-
Структура программного обеспечения ПО функционирует в реальном масштабе времени с прерываниями от сети (TRAP) и таймера (RST 7.5). Структура программного...
-
Структура дослідження інтеракційного та трансакційного полів розподілу доходів в моделі одиничної економіки агрегованого ринку Інституційний аспект...
-
В данном разделе речь идет об особом уровне развития химических знаний, на котором главенствующую роль играет структура молекулы реагента. Свойства...
-
КОНТАКТНОЕ ОКИСЛЕНИЕ ДИОКСИДА СЕРЫ. - Получение серной кислоты
Реакция (III) окисления диоксида серы характеризуется очень высоким значением энергии активации и поэтому практическое ее осуществление возможно лишь в...
-
Зонная структура арсенида индия Зона проводимости Арсенид индия является прямозонным полупроводником, у которого зона проводимости сферически симметрична...
-
II семестр §1. Евклидово пространство Евклидово пространство - это линейное пространство с некоторым образом введенной операцией "скалярного...
-
Математическое ожидание, дисперсия Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными...
-
Дипольный момент молекулы и связи
Представим себе, что можно найти "центры тяжести" отрицательных и положительных частей молекулы. Тогда условно все вещества можно разбить на две группы....
-
Топологический элементный анализ - Системная революция и принцип дуального управления
Независимые от системы элементы формально выглядят как изолированные вершины графа структуры (ее симплекса). Если некоторый элемент на всех структурах...
-
Введение - Моделирование крупномасштабной транспортной сети предфрактальными графами
Транспорт - важный стратегический комплекс, в значительной степени определяющий мощь экономики страны и обеспечивающий нужды общества в перемещении людей...
-
Пусть у нас имеется некоторая непрерывная случайная величина X, распределенная нормально с математическим ожиданием и среднеквадратичным отклонением....
-
Проводя на практике анализ мезо среды поступают следующим образом: производится оценка динамики количественных значений показателей состояния...
-
Організаційно-функціональна структура представлена на Рис. 1.1. Керівництво поточною діяльністю ВАТ здійснює Правління, до складу якого входять:...
-
Сельское хозяйство относится к числу сложных экономических систем. Расширенное воспроизводство в сельском хозяйстве представляет собой взаимосвязь...
-
Прототипом разработанной автором системы моделей служит "точечная" модель [1], представляющая собой пространственно осредненный вариант уравнений горения...
-
Целью работы является моделирование на ПЭВМ с помощью инструментария Simulink замкнутой системы автоматического регулирования (САР) по заданному...
-
Структура створюваних моделей Основний виробничий процес - це система трьох складових: постачання сировини, виробництво і збут продукції (Рис. 2.1.)....
-
В структурном виде данную экономико-математическую модель можно представить следующим образом: Минимизировать значение функции: Выводы и предложения....
-
В данной задаче за основные неизвестные приняты площади посева сельскохозяйственных культур по их целевому назначению и площади сенокосов и пастбищ. Х1...
-
Організаційна структура підприємства ЗАТ "Годинникар" є юридичною особою і діє на підставі статуту і законодавства України. Підприємство створено...
-
Научная теория и ее структура - Основы научных исследований
Теория - система логически непротиворечивых верифицируемых высказываний, в идеале имеющая аксиоматическую структуру и полностью соответствующая всем...
-
Для разработки экономико-математической модели данной задачи необходимо подготовить следующую информацию: Размер площади пашни, пастбищ и сенокосов;...
-
Таблица 1.3.1 Отгружено продукции (услуг) Отгружено товаров собственного производства, выполнено работ и услуг собственными силами 2006 2007 Тыс. руб. %...
Об инфинитезимальных изометриях продолженных почти контактных метрических структур