Двумерная математическая модель жидкости водоема с учетом наличия на поверхности ледяной пластины
Введение
В данной работе рассматривается численная модель движения в двумерных (в вертикальной плоскости) водоемах. Математическая модель основана на уравнениях Навье-Стоксавприближениях. Для построения численного алгоритма применяются метод расщепления по физическим процессам.
1. Постановка задачи
Рассматривается задача волновой динамики жидкости. Исходными уравнениями являются:
- уравнение Навье-Стокса:
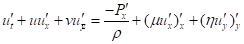
; (1)
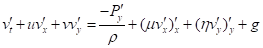
. (2)
- уравнение неразрывности:
Жидкость математический ледяной алгоритм
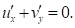
(3)
Уравнения (1) - (3) рассматриваются при следующих граничных условиях, где для разных границ данной области жидкости отдельные условия
- на дне водоема:
(4)
- на свободной поверхности жидкости:
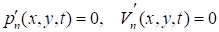
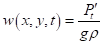
, ; (5)
- на поверхности жидкости, покрытой ледяной пластиной:
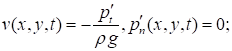
, ,
,
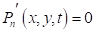
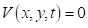
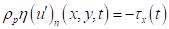
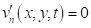
- - на входе задается поток от источника: - на выходе:
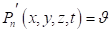
, ; ,
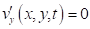
- начальные условия: при моменте выполняются следующие условия:
, ,,
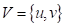
Где - вектор скорости движения водной среды, - давление, - коэффициент турбулентного обмена по горизонтальному направлению,- коэффициент турбулентного обмена по вертикальному направлению, - ускорение свободного падения, - плотность жидкости, - составляющая тангенциального напряжения (закон Ван-Дорна), - плотность суспензии(взвеси). Система координат выбрана таким образом, что ось совмещена с дном водоема и направлена в сторону ледовой пластины, ось - вертикально вверх.
Имеются разные временные слои два реальных при, и один промежуточный слой при соответственно можно обозначить
, , , .
Расщепляя уравнения (1), (2), по физическим процессам, получим:
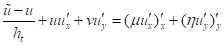
, (6)
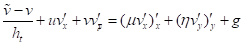
, (7)
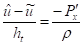
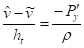
,, (8)
После дифференцирование по и уравнения (18), (18), (20) примут вид:
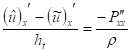
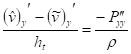
, , (9)
Суммируя уравнения (9), учитывая уравнение неразрывности (3)получим уравнение:
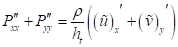
(10)
Расчет задач гидродинамики по данному методу осуществляется в три этапа. На первом этапе считается поле скоростей. На втором этапе рассчитывается давление. На третьем этапе уточняется поле скоростей по давлению.
Для аппроксимации задачи применяется интегро-интерполяционный метод, по области:
, :
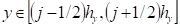
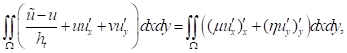
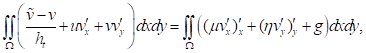
Уравнение (11) и (12) представляет собой конечно-разностную схему для уравнения (6) и (7).
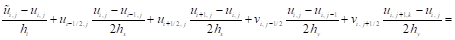
(11)
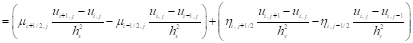
Аналогично:
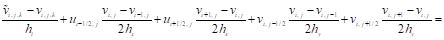
(12)
.
Для аппроксимации операторов диффузии и конвекции по временной переменной будем использовать схемы с весами.
Также проинтегрируем уравнение (10) по области :
, :
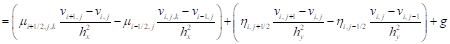
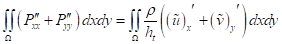
. (13)
Тогда уравнение запишется в виде:
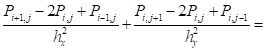
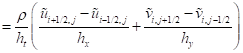
. (14)
Проинтегрируем уравнение (9) по области :
, :
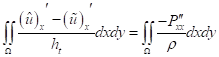
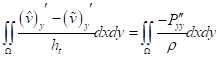
,,. (15)
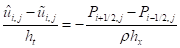
. (16)
Аналогично можно записать конечно-разностную схему для уравнения:
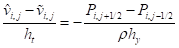
, (17).
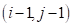
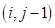
Дискретная конечно-объемная модель волновой гидродинамики. Расчетные ячейки представляют собой прямоугольники, они могут быть заполненными, частично заполненными или пустыми. Центры ячеек и узлы разнесены на, и по координатам и соответственно. Обозначим через заполненность ячейки. Поле скоростей и давление рассчитываются в вершинах ячейки. Вершинами ячейки являются узлы, , , .
Степень заполненности ячейки определяется давлением столба жидкости внутри данной ячейки. Если среднее давление в узлах, которые относятся к вершинам рассматриваемой ячейки, больше давления столба жидкости внутри ячейки, то ячейка считается заполненной полностью. В общем случае заполненность ячейки можно вычислить по следующей формуле:
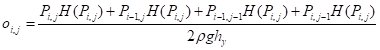
(18)
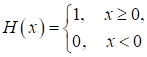
Где - функция Хевисайда.
В окрестности узла лежат ячейки, , , .
Введутся коэффициенты, , , , , описывающие заполненность областей, находящихся в окрестности ячейки. Значение, характеризует заполненность всей области
Заполненные части областей будем называть, где. В соответствии с этим коэффициенты можно вычислить по формулам:
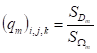
,
А уравнение (11) примет вид:
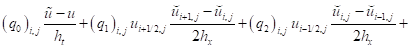
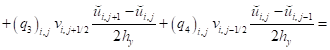
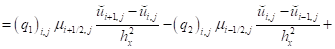
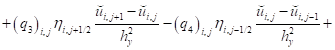
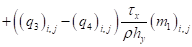
Также уравнение (12):
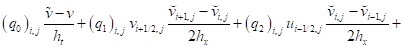
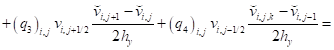
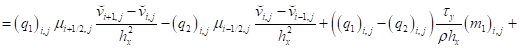
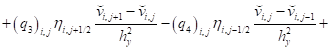
. (19)
Далее представляется следующие сеточные уравнения:
- для составляющей вектора скорости :
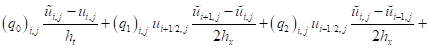
, (20)
- для составляющей вектора скорости :
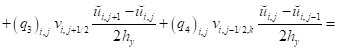
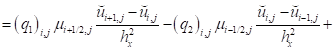
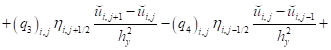
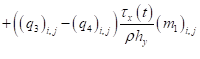
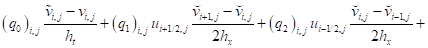
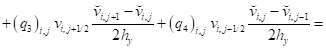
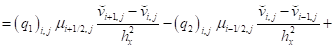
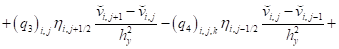
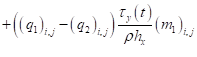
; (21)
- сеточными уравнениями для расчета поля давления:
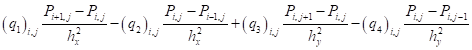
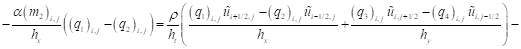
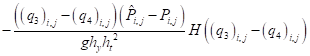
; (22)
- уравнениями для уточнения поля скоростей по давлению:
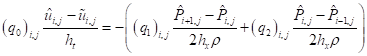
, (23)
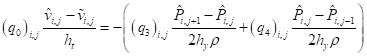
, (24)
Где параметр, :. "маски" граничных условий.
Таким образом, построена конечно-объемная модель задачи волновой гидродинамики, представленная уравнениями (20) - (25).

Рис. 1 Поле вектора скоростей жидкости
Результаты численных экспериментов расчета движения водной среды, частично покрытой ледяной пластиной представлены на рис. 1, где изображена динамика набегающего к пластине потока воды.
Полученная модель, проектируемая для расчетной области с заданными численными значениями, являющимися размером сетки с шагами по оси x и y соответствующимиhx, hy.
Заключение
Разработана двумерная математическая модель для расчета полей скоростей; приведено описание программной реализации математической модели для расчета полей скоростей водной среды; выполнен численный эксперимент, построена картина потока воды водоема при наличии ледового покрытиявпериодов времени, которые согласуются с реальным физическим процессом.
Литература
- 1. Самарский А. А., Михайлов А. П. Математическое моделирование: Идеи. Методы. Примеры. М.: Физматлит, 2001. 320 с. 2. Стокер, Дж. Дж. Волны на воде. Пер. с англ. - М. : Иностр. литер., 1959. 618 с.
Размещено на Аllbеst. ru
Похожие статьи
-
Классификация математических моделей - Построение и классификация математических моделей
К классификации математических моделей разные авторы подходят по-своему, положив в основу классификации различные принципы. Можно классифицировать...
-
Вводим дополнительные ограничения в модель: А) продукция типа 1 выпускается только в том случае, если разрешен выпуск хотя бы одного типа продукции: 2 и...
-
На основании вышеприведенных обозначений сформулируем математическую модель задачи оптимизации графиков занятости работников с многосменной организацией...
-
Математическое моделирование - Основы научных исследований
Выше уже указывалось, что Математическое моделирование - это получение решений уравнений, составляющих математическую модель объекта, при изменении...
-
В решении любой прикладной задачи можно выделить три основных этапа: - Построение математической модели исследуемого объекта - Выбор способа и алгоритма...
-
В воздушном зазоре электрических машин всегда, наряду с основной гармонической составляющей вращающегося магнитного поля, присутствуют гармонические...
-
Проверить ряд на наличие выбросов методом Ирвина, сгладить методом простой скользящее средней с интервалом сглаживания 3, методом экспоненциального...
-
Любой электромеханический преобразователь можно рассматривать в установившемся и динамическом режиме. Модель в установившемся режиме, по сути, является...
-
МК (рисунки 6 и 7) представляет собой ПУ включающий в себя мостовую схему управления электродвигателем с элементами управления ключами моста, токовые...
-
Теоретическое обоснование математического моделирования - Математические методы и модели в экономике
Коммерческая деятельность в том или ином виде сводится к решению таких задач: как распорядиться имеющимися ресурсами для достижения наибольшей выгоды или...
-
Для заданного региона обслуживания с помощью технологии ГИС предоставляется карта автомобильных дорог, на которой указаны пункты, соответствующие...
-
Важнейшие математические модели обычно обладают важным свойством Универсальности : принципиально разные реальные явления могут описываться одной и той же...
-
В статье разработана и приведена математическая модель задачи оптимизации количества персонала предприятий, работающих посменно и с разным графиком...
-
1. Универсальность - характеризует полноту отображения моделью изучаемых свойств реального объекта. 2. Адекватность - способность отражать нужные...
-
Z -преобразование является одним из математических методов, разработанных для анализа и проектирования дискретных систем. Аппарат Z -преобразования...
-
Уравнение динамики теплообменника: Передаточные функции объекта получим по его уравнению динамики. Для этого запишем уравнение по заданному каналу. Затем...
-
Необходимо составить математическое описание теплообменника, в котором жидкий продукт нагревается насыщенным водяным паром (расход, кг/с), до температуры...
-
Введение - Моделирование математической модели теплообменника
Математический динамический модель канал Качественные и количественные изменения в промышленности, науке и технике составляют основу для значительного...
-
В большинстве случаев структурная неопределенность вызвана неполнотой знания аналитической структуры уравнений модели объекта управления. При не...
-
Для определения и проведения экспериментальных исследований Тепловых режимов ЭРИ, разработаем топологическую математическую модель блока управления...
-
Уровень науки и техники Надежность средств, с помощью которых человек достигает космоса высокая, но не идеальна. РН -- сложная конструкция, и даже в...
-
С началом пилотируемого освоения космоса возникла задача обеспечения безопасности человека и возвращения его на Землю. Основная опасность грозила...
-
Модель парной линейной регрессии - Математическое описание связи: регрессия, корреляция
Предположим, что у нас есть все основания считать, что два экономических показателя взаимосвязаны. Например, уровень инфляции и уровень безработицы в...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
В 1974г. группа аргентинских ученых во главе с профессором А. Эррерой получила предварительные результаты работы над латиноамериканской моделью...
-
Система "Диспетчер" апробирована на реальных исходных данных двух регионов Нефтяной Компании "Юкос" (Липецкая и Воронежская области) и показала свою...
-
Адсорбция активированный уголь Развитие теории адсорбционных сил еще не достигло такой стадии, когда по известным физико-химическим свойствам газа и...
-
Практически все авторы, описывающие процесс математического моделирования, указывают, что сначала строится особая идеальная конструкция, Содержательная...
-
В работе рассматривается задача нахождения маршрутов развоза товаров на объекты заданного региона, возникающая у компаний, желающих сократить...
-
Заключение, Список использованной литературы - Моделирование математической модели теплообменника
В данной курсовой работе была получена математическая модель теплообменника в виде дифференциальных уравнений. Также была получена передаточная функция...
-
Выделим случай, когда входной сигнал X ( T ) является элементарной функцией 1( T ). Реакцию системы на воздействие 1( T ) можно компактно: [1] Где...
-
Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования
Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования Современная автомобильная промышленность ставит перед...
-
В качестве примера конкретной модели процесса управления обсудим модель распределения времени между овладением знаниями и развитием умений, впервые...
-
Классификация моделей - Математическое моделирование в менеджменте и маркетинге
Классифицировать модели можно по разным критериям. Например, по характеру решаемых проблем модели могут быть разделены на функциональные и структурные. В...
-
При управлении подвижными объектами (такими, например, как мобильные роботы, подводные аппараты и т. п.) часто имеет место неопределенность цели, когда...
-
Экспериментальная факторная модель процесса акусто-магнитной обработки топлива
Всевозрастающее воздействие человека на природу привело к возникновению экологических проблем в экосистеме биосферы, в частности, проблемы загрязнения...
-
Моделирование процессов управления предполагает последовательное осуществление трех этапов исследования. Первый - от исходной практической проблемы до...
-
Маркетинговое исследование представляет собой системный сбор, обработку и анализ всех аспектов процесса маркетинга: продукта, его рынка, каналов...
-
Введение - Эконометрические модели маркетинговой деятельности на предприятии
Процесс моделирования имеет несколько этапов. Содержательная постановка задачи - формулируются вопросы, на которые надо получить ответы. Делаются...
-
Методы построения решений по математическим моделям - Математическое моделирование в электромеханике
Системы дифференциальных уравнений, полученные для конкретных ти-пов электрических машин, содержат в скрытом виде исчерпывающую инфор-мацию о всех...
Двумерная математическая модель жидкости водоема с учетом наличия на поверхности ледяной пластины