Диференціальні властивості тригонометричних поліномів, що апроксимують задану функцію - Дослідження якнайкращих наближень безперервних періодичних функцій тригонометричними поліномами
У цьому параграфі встановлюється, що якщо тригонометричний поліном Tn(x) Близький до заданої функції F, то його модулі безперервності можна оцінити через модулі безперервності F.
Теорема 3. Зафіксуємо натуральні числа До І N І хай
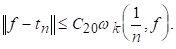
(5.1)
Тоді для будь-якого
(5.2)
(5.3)
(5.4)
І
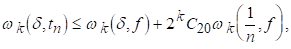
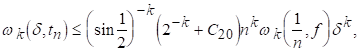
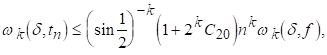
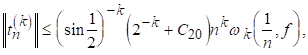
(5.5)
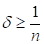
Попередні зауваження. Нерівності (5.2) і (5.4) переважно для великих d, а (5.3) - для малих. Якщо то (5.2) сильніше, ніж (5.4); проте (5.4) має більш симетричну форму і часто зручніше в додатках.
Доказ. Доведемо (5.2). Користуючись (2.1), (2.2) і (5.1), маємо
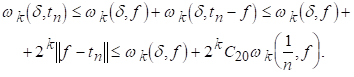
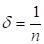
Доведемо (5.5). Покладемо в (5.2) . Тоді отримаємо :
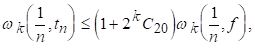
Після чого (4.5) дає (5.5).
(5.3) виходить з (5.5) в силу (2.11).
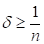
Залишається довести (5.4). Хай спершу. Тоді з (5.4) слідує:
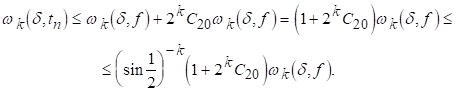
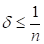
Розглянемо, нарешті, випадок. З нерівності (2.7) виводиться
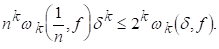
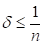
Підставляючи цю оцінку в (5.3), отримуємо (5.4) для.
Таким чином, теорема повністю доведена.
Слідство 3.1. Хай для деякого натурального До І будь-якого натурального N
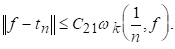
(5.6)
Тоді для будь-якого d>0
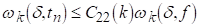
(5.7)
Рівномірно відносно N.
Слідство 3.2. Хай для деякого натурального До І будь-якого натурального N
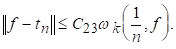
Тоді
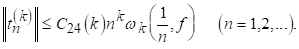
(5.8)
Теорема 4. Для того, щоб необхідно і достатньо, щоб
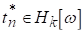
(5.9)
Рівномірно відносно N.
Це витікає з теореми 1, следствия 3.1 і того зауваження що якщо виконана умова (5.9), то.
Теорема 5. Для того, щоб необхідно і достатньо, щоб
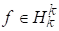
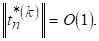
(5.10)
Це доводиться аналогічно теоремі 4, тільки замість слідства 3.1 потрібно скористатися слідством 3.2.
Нерівності теореми 3 мають той недолік, що їх праві частини явно залежать від константи С20. Таким чином, якщо замість фіксованого номера N І одного полінома Tn розглядати послідовність поліномів {Tn} (N=1,2...), то С20 опиниться, взагалі кажучи, незалежною від N І теореми 3 дає оцінки, не рівномірні відносно N. Покажемо як позбавитися від цієї незручності.
Теорема 6. Хай для деякого натурального до
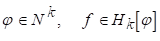
(5.11)
І
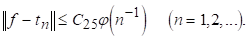
(5.12)
Тоді для будь-якого d>0
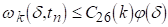
(5.13)
Рівномірно відносно N.
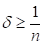
Доказ. Хай спершу. З нерівності (5.2) виходить, що
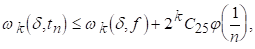
І на підставі (5.11)
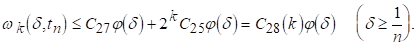
(5.14)
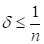
Розглянемо випадок. Покладемо в (5.14) . Тоді отримаємо
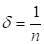
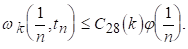
З цієї нерівності, в силу, витікає, що
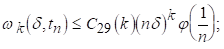
Але оскільки, по умові то
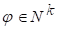
Звідси
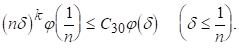
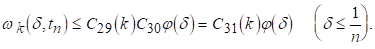
Остаточно
І теорема доведена.
У наступному параграфі буде показано, як можна видозмінити обмеження (5.11) теореми 6.
Похожие статьи
-
Звернемося тепер до розгляду наступного питання: які необхідні і достатні умови того, щоб Де - задана незростаюча функція? Наскільки нам відомо, це...
-
У цьому параграфі узагальнюються і уточнюються так звані "зворотні теореми" теорії наближення. Мова йде про оцінці диференціальних властивостей функції f...
-
Тут буде отримано невелике посилення теореми Джексона про якнайкращі наближення періодичних функцій тригонометричними поліномами. Лема 7. Хай дано...
-
Цей параграф носить допоміжний характер. Тут встановлюється декілька простих властивостей модуля нерперывности вищих порядків. Всі функції F1 , що...
-
У цьому параграфі формулюється одне узагальнення нерівності С. Н. Бернштейна для похідних від тригонометричного полінома. Теорема 2. Хай. Тоді для...
-
Дипломна робота присвячена дослідженню якнайкращих наближень безперервних періодичних функцій тригонометричними поліномами. У ній даються необхідні і...
-
У роботі розглядаються безперервні функції F З періодом 2p і їх наближення тригонометричними поліномами. Через Tn(x) Позначається тригонометричний...
-
Приклад 1. Хай Тоді при кожному Приклад 2. Хай графік функції F(x) Має вигляд, зображений на рис.8.1. Тоді графік функції показаний на рис.8.2. Мал. 8.1....
-
Теорема 1. Похідна від функції logax дорівнює, тобто якщо y=logax, то . (11.1) Теорема 2. Похідна від sinx є cosx, тобто якщо y=sinx, то Y =cosx. (11.2)...
-
Теорема Маркова - Невід'ємні матриці
Нехай для стохастичної матриці P існує натуральне число k0 таке, що (тобто всі елементи додатні). Тоді 1. (існування границі матриці означає, що існує...
-
Нехай функція F (х) задана на відрізку [a, b] . Розіб'ємо цей відрізок на N частин точками ділення А = х0 < x1 < x2 < ... < хn = b У кожному...
-
Дослідження функції однієї змінної за допомогою першої й другої похідних - Основи вищої математики
I. Ознаки сталості зростання й спадання функції Теорема 1. Якщо у всіх точках проміжку A < X < B похідна F ( Х) = 0, то функція F ( Х) зберігає в...
-
Теорема 1. Похідна Const =0, тобто якщо Y = С, те Y =0, де С = Const . Y = С -- пряма паралельна осі ОХ й Tg =0, тобто F ( Х) =0. Теорема 2. Постійний...
-
Загальні властивості функцій - Функції та способи їх задання
Означення : Множина всіх значень аргумента, для яких можна обчислити значення функції, називається природною областю визначення функції. Область...
-
Межа функції - Основи вищої математики
Розглянемо деякі випадки зміни функції або прагнення аргументу Х до деякої межі " А " або до. Визначення 1: Нехай функція y=f(х) визначена в деякій...
-
Вступ, Необхідні відомості з теорії матриць - Невід'ємні матриці
Відомо [[1]-[10]], яку важливу роль відіграють невід'ємні матриці в математичних моделях економіки, біології, теорії ймовірностей тощо. Одними з...
-
Визначення : Скалярний добуток двох векторів і дорівнює добутку модулів цих векторів на косинус кута між ними . (6.1) Таким чином, скалярний добуток двох...
-
Визначники та їх властивості - Основи вищої математики
До поняття визначника приходимо, розглядаючи системи алгебраїчних рівнянь першого степеня. Розглянемо систему рівнянь: (2.1) X та y -- невідомі,...
-
Теорема 1. Нехай послідовності (хП) і (уП) мають відповідно границі а і b. Тоді послідовність (xN+yN) має границю а + b. Теорема 2. Нехай послідовності...
-
Положення підприємства багато в чому визначається його фінансовим станом, у зв'язку з чим аналізові фінансових результатів діяльності надається велике...
-
Диференціал, Визначення диференціала. - Основи вищої математики
Визначення диференціала. Формули й правила диференціювання. Використання диференціала для наближених обчислень. Основні теореми диференціального...
-
Зв'язок між визначеним та невизначеним інтегралами Означення 2. Визначений інтеграл з постійною нижньою межею та змінною верхньою межею називають...
-
Асимптоти. Вертикальні й горизонтальні - Основи вищої математики
Якщо відстань ОМ від деякої точки О до точки, що Рухається, М, то Відстань О 1 М , на яку Точка М віддаляється від якої-небудь іншої нерухомої Крапки О 1...
-
Точки розриву і їхня класифікація. Теореми про безперервні функції - Основи вищої математики
Якщо функція F така, що для неї існують межі F ( А +0) і F ( А --0), однак F ( А ) F ( А +0) F ( А --0), то, мабуть, вона нерозривна (не безперервна) у...
-
Розкриття невизначеностей. Формула Тейлора - Основи вищої математики
1. Невизначеність виду 0/0. Теорема 1 ( Правило Лопіталя - Гійом 1661-1704 р., французький математик, автор першого друкованого підручника по...
-
Щоб значно спростити задачу транспортування і подальшого зберігання газу, його необхідно зріджувати. Додаткова умова - це охолодження природного газу,...
-
Теоретичні основи оптимізаційних рішень Умови оптимальності у формі принципу максимуму дають, узагалі говорячи, достатню інформацію для рішення задачі...
-
Задачі, що привели до поняття визначеного інтеграла Розглянемо дві задачі -- геометричну та фізичну. 1. Обчислення площі криволінійної трапеції . Нехай...
-
Попит і пропозиція - економічній категорії товарного виробництва. Попит - представлена на ринку потреба в товарах, Пропозиція - продукт, який є на ринку...
-
Визначення : Сукупність лінійно незалежних векторів, по яких відбувається розкладання інших векторів, називається Базисом . Отже, у площині можуть...
-
Поняття математичного моделювання - Математичне моделювання та диференціальні рівняння
Поняття математичного моделювання трактується різними авторами по своєму. Ми будемо його пов'язувати з нашою спеціалізацією - прикладна математика. Під...
-
З математичної точки зору розв'язки (1) і (2) мають однаковий зміст. О-1 Подвійним інтегралом від функції по області називається границя (3) За умови, що...
-
Впровадженню ARIS обов'язково повинна передувати серйозна "ручна" проектно - аналітична робота. У методології ARIS все розподілено, розмежовано і...
-
Система диференціальних рівнянь, що записана у вигляді Чи у векторно-матричному вигляді Називається системою лінійних неоднорідних диференціальних...
-
Результаты исследований А. Н. Фрумкина и Б. В. Дерягина показали, что характер изменения удельной поверхностной энергии е прослоя воды, находящегося...
-
Визначення : Алгебраїчні лінійні рівняння називаються однорідними, якщо в них вільний член дорівнює нулю. Розглянемо таку систему, що має вигляд: (10.1)...
-
ВУГЛЕКИСЛИЙ ГАЗ ТА ЙОГО ВЛАСТИВОСТІ - Склад повітря
Вивчаючи "Склад повітря" ми проводили дослід, зображений на малюнку 41. Через те, що вапняна вада помутніла ми зробили висновок, що у повітрі є...
-
Так як підприємство має інвестиційні ресурси, що можуть бути вкладені тільки в один з проектів, то для дослідження ефективності розподілу інвестиційних...
-
Графіки перехідних процесів, отримані шляхом моделювання: Момент двигуна, Нм Кутова швидкість ротора, рад/с Модуль потокозчеплення статора, Вб Модуль...
-
Рівняння, Трансцендентні рівняння - Основи вищої математики
З одним невідомим повинно бути одне, його звичайно приводять до канонічного вигляду: Приклад: Рівняння 1,2,3 ... степені і т. д. -- лінійні рівняння....
Диференціальні властивості тригонометричних поліномів, що апроксимують задану функцію - Дослідження якнайкращих наближень безперервних періодичних функцій тригонометричними поліномами