Анализ факторов, обуславливающих успех управления маркетингом, Оценка значимости местонахождения пункта продаж на средние цены автомобилей - Решение исследовательских задач
Оценка значимости местонахождения пункта продаж на средние цены автомобилей
При воздействии на систему множества факторов (оцениваемых количественно или качественно) устанавливается связь между ними и признаком. Факторы - независимые случайные переменные, признак - зависимая случайная переменная. В качестве характеристики изменения признака используется полная дисперсия. Задача дисперсионного анализа - разложение полной дисперсии на составляющие:
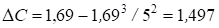
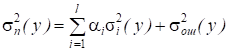
, (2.1)
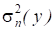
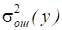
Где - полная дисперсия, характеризующая изменчивость признака у в данной серии экспериментов; - составляющая полной дисперсии, обусловленная изменчивостью i-го фактора или взаимодействия факторов; бi - коэффициент, характеризующий объем наблюдений; - дисперсия, характеризующая ошибку эксперимента и действие неучтенных факторов
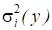
Для решения вопроса о том, существенно ли влияние данного фактора на признак, используется критерий Фишера:
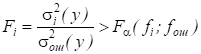
, (2.2)
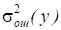
Где б - уровень значимости, характеризующий вероятность, с которой определяется существенность исследуемого фактора; fi - число степеней свободы дисперсии (у), характеризующее количество информации, использованное для ее вычисления; fош - число степеней свободы дисперсии, характеризующее количество информации, использованное для ее определения, т. е. значимость оценивается на фоне шумового поля, создаваемого действием неучтенных факторов и ошибки эксперимента.
Модель однофакторного дисперсионного анализа
Уik = м + Ai + еik, (2.3)
Где уik - значение признака у, когда фактор А находится на i-м уровне при k-м повторении опыта; м - математическое ожидание признака у, оценка которого вычисляется по результатам всех наблюдений; Аi - влияние на изменчивость признака фактора А, когда он находится на i-м уровне (эффект фактора А); еik ошибка эксперимента и действие неучтенных факторов, когда фактор А находится на i-м уровне при k-м повторении опыта.
Для проведения анализа необходимо фактору А придавать различные значения, т. е. исследовать на различных уровнях i, i = 2, 3,..., а; аmin = 2; k - число наблюдений на каждом уровне, k = 3, 4, ..., n; kmin = 3. В случае однофакторного дисперсионного анализа общее число наблюдений N = a - n.
Проведя опыты, можно найти общую среднюю и средние значения по уровням наблюдений и определить суммарные квадраты.
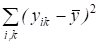
Q = - полный суммарный квадрат, характеризующий полную изменчивость признака.
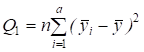
- суммарный квадрат, характеризующий отклонения групповых средних от общей средней, он определяет изменчивость признака от действия фактора А и межгрупповой ошибки эксперимента, число степеней свободы f1 = a - 1.
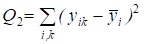
- суммарный квадрат, характеризующий ошибку эксперимента и действие неучтенных факторов внутри групп наблюдений.
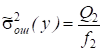
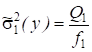
Поскольку опыты производятся в однородных условиях (это предпосылка проведения дисперсионного анализа), то межгрупповая дисперсия ошибки эксперимента и действия неучтенных факторов и общая дисперсия ошибки эксперимента и действия неучтенных факторов однородны. По сути, это одна и та же дисперсия, оценки которой вычисляются по разному объему выборок из одной и той же совокупности экспериментальных данных, поэтому ее оценка, где f2 - число степеней свободы, f2 = N - a. Учтя это и определив оценку дисперсии, можно записать
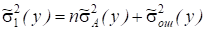
,
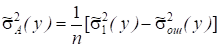
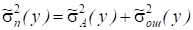
Откуда и. (2.4)
Вклад фактора в изменчивость признака вычисляется по формуле
Ввкл = [S2A(y)/S2п(у)]-100 %, (2.5)
Где S2A(y), S2п(y) - соответственно оценка дисперсии, характеризующая вклад фактора в изменчивость признака, и полная дисперсия, характеризующая полную изменчивость признака.
Расчетные зависимости для рационального подсчета численных значений суммарных квадратов имеют вид
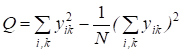
; ;
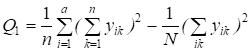
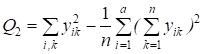
. (2.6)
Пример. По данным источника [13] исследовать влияние местонахождения пункта продаж (Минск, Москва) на средние цены (тыс. долл США) легковых подержанных автомобилей марок БМВ, "Опель-Астра", "VW-Гольф", "Форд-Мондео" в ноябре 2000 г., имеющих в первом приближении одинаковое техническое состояние.
В табл. 13 приведены цены на автомобили в Минске и Москве, а также необходимые расчетные параметры.
Таблица 13 - Вычисление показателей для расчета влияния местонахождения пункта продаж на средние цены подержанных автомобилей
|
№ п/п |
Местонахождение пункта продаж |
Суммы | |
|
Минск |
Москва | ||
|
1 |
2 |
3 |
4 |
|
1 |
5,0 |
6,8 | |
|
2 |
3,1 |
4,1 | |
|
3 |
2,3 |
5,0 | |
|
4 |
4,1 |
5,1 | |
|
5 |
5,3 |
7,2 | |
|
6 |
2,8 |
4,2 | |
|
1 |
2 |
3 |
4 |
|
7 |
3,4 |
5,4 | |
|
8 |
3,8 |
5,4 | |
|
I |
3,7 |
5,4 | |
|
J |
1,1 |
1,2 | |
|
Уу |
29,8 |
43,2 | 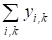
= 73 |
|
Уу2 |
118,6 |
241,9 | 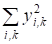
= 360,5 |
|
(Уу)2 |
888,0 |
1866,2 | 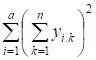
= 2754,2 |
Решение. Приведенные значения параметров вычисляют по следующим формулам:
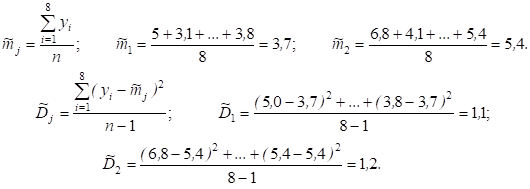
Вначале проверяют однородность оценок дисперсий по уровням наблюдений. Вычисляют значение F-статистики:
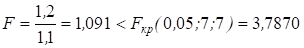
.
Следовательно, оценки дисперсий однородны, дисперсионный анализ можно проводить, поскольку с достаточным уровнем доверительной вероятности неучтенные факторы и неизбежная ошибка эксперимента существенно не повлияли на изменчивость признака.
Значения сумм для первого столбца данных (Минск):
Уу = 5,0 + 3,1 + ...+ 3,8 = 29,8;
Уу2 = 5,02 + 3,12 +...+ 3,82 =118,6;
(Уу)2 = 29,82=888,0.
Для второго столбца (Москва):
Уу = 6,8 + 4,1 +...+ 5,4 = 43,2;
Уу2 = 6,82 + 4,12 +...+ 5,42 = 241,9;
(Уу)2 = 43,22 = 1866,2.
Для третьего столбца (суммы):
= 29,8 + 43,2 = 73;
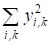
= 118,6 + 241,9 =360,5;
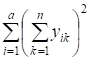
= 888,0 + 1866,2 =2754,2.
Вычисляют значения суммарных квадратов:
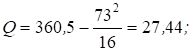
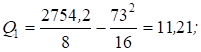
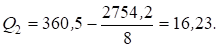
Оценка дисперсии, характеризующая изменение признака от воздействия фактора (местонахождения пункта продаж) и внутригрупповой ошибки эксперимента и действия неучтенных факторов при числе степеней свободы f1 = a - 1 = 2 - 1 = 1
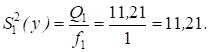
Оценка дисперсии, характеризующей воздействие на признак ошибки эксперимента и действия неучтенных факторов при числе степеней свободы f2 = N - a = 16 - 2 = 14
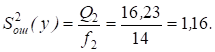
Значимость фактора (местонахождения пункта продаж) оценивается F-критерием при уровне значимости б = 0,05 и числах степеней свободы f1 = 1 и f2 = 14 (табл. 10 приложения), проверяется нулевая гипотеза Н0: S21(y) > S22(y) при конкурирующей Н1: S21(y) ? S22(y):
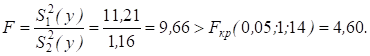
Поскольку значение F-статистики превышает критическое значение Fкр, гипотеза о существенности фактора не отвергается.
Значение оценки дисперсии S2А(у):
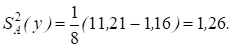
Величина оценки полной дисперсии
S2п(у) = 1,26 + 1,16 = 2,42.
Вклад фактора - местонахождения пункта продаж автомобилей - в формирование цены на подержанный автомобиль
Ввкл = (1,26 / 2,42)100% = 52 %.
Следовательно, цена на подержанный автомобиль на 52% зависит от места нахождения пункта продаж.
Похожие статьи
-
Модель двухфакторного дисперсионного анализа имеет вид , (2.7) Где уijk - значение признака у, когда фактор А находится на i-м уровне, фактор В - на j-м...
-
В случае проверки эффективности рандомизации (целью которой является исключение существенного влияния на исследуемый объект систематически действующих...
-
Оценка однородности условий маркетинговой деятельности - Решение исследовательских задач
Все этапы маркетинга как деятельности, направленной на удовлетворение нужд и потребностей людей, от производства товаров до потребления зависят от...
-
Пример. Исследовать влияние квалификации специалистов, привлекаемых к проведению технических обслуживаний (ТО) машин, на продолжительность ТО....
-
Для проверки гипотезы об однородности двух выборок о1, о2, ... оn и ог1, ог2, ... огm c независимыми элементами используют критерий Вилкоксона W....
-
Для оценки наличия и тесноты связи между двумя объектами, свойства которых описываются качественными показателями, используют метод ранжирования,...
-
Для оценки однородности средних значений независимых нормально распределенных величин, дисперсии которых равны (однородны), но неизвестны, может быть...
-
От 50 до 90 % статистических данных, используемых в экономике, социологии, медицине, технике, имеют нечисловую природу и могут быть оценены только...
-
Экспертные методы оценивания качества товаров и услуг При оценивании качества товаров как совокупности трудно измеряемых свойств очень часто прибегают к...
-
Предпосылки использования в маркетинговых исследованиях статистических методов При исследованиях показателей маркетинговой деятельности в реальных...
-
Совершенно очевидно, что благополучие компании "Poligraf" зависит не только от деятельности самой компании и ее сотрудников, но и от противоборства...
-
Управление запасами, Термины, постановка задачи - Решение исследовательских задач
Термины, постановка задачи Основной предмет изучения - связь между Q - количеством запаса на складе и временем, для которого рассматривается этот запас...
-
Анализ внешних факторов конкурентоспособности Конкурентные преимущества, безусловно, способствуют привлечению внимания к предприятиям общепита целевых...
-
Объем продаж товаров в плане определяется как стоимость предназначенных к поставке и подлежащих оплате в плановом периоде: готовых изделий;...
-
Введение - Решение исследовательских задач
Маркетинг как вид человеческой деятельности, направленной на удовлетворение нужд и потребностей посредством обмена [7], подвержен влиянию огромного...
-
Методы оценки конкурентоспособности товаров и услуг Разработка проблемы конкурентоспособности товаров и услуг напрямую зависит от выбранного метода...
-
Воронка продаж Расчет эффективности проведенной рекламной кампании целесообразно осуществить с помощью воронки продаж (рис.1).[2] Воронка продаж - это...
-
В настоящее время многие руководители кыргызстанских компаний пытаются внедрить стратегическое управление в деятельность своих организаций,...
-
Конкурентоспособность товара -- его интегральное свойство, обусловливающее способность товара удовлетворять требованиям покупателей к его составляющим по...
-
Сбыт потребитель доход маркетинговый Для предварительного выявления наличия связи и раскрытия ее характера можно применить графический метод. Используя...
-
При анализе внутренних факторов конкурентоспособности использовалась модель 5 конкурентных сил Майкла Портера - достаточно старая и известная модель...
-
Применение методологии проектирования внутрипроизводственных логистических систем при решении практических задач Методология - учение о методах, способах...
-
Цели и задачи анализа продаж продукции - Анализ реализации продукции предприятия
Производственная организация - это пространственно-временная структура производственных факторов, обеспечивающая их взаимодействие с целью получения...
-
Текущая мировая ситуация диктует свои условия развития грузовых перевозок железнодорожным компаниям. Провозглашается стремление к открытости и...
-
Конкурентоспособность товара, прежде всего, определяется его качеством. Качество - критерий оценки товара, объединяющий комплекс требований к нему....
-
Стратегический анализ Сегментный анализ 1) Проверка правильности используемых признаков сегментации с помощью непараметрических критериев. При сегментном...
-
Анализ факторов, определяющих конкурентоспособность - Конкурентоспособность предприятия
Факторы конкурентоспособности услуги подразделяются на внешние, проявление которых в малой степени зависит от организации, и внутренние, почти целиком...
-
Оценка эффективности процесса продаж - Автоматизация продаж
Любой бизнес-проект требует хорошего экономического обоснования и хорошего управления данными. Особенно это актуально для определения эффективности...
-
Оценка значимости показателей качества Исследуемым изделием является мужские полуботинки, основным назначением которой является повседневная носка, для...
-
В торговый зал магазина товары должны поступать полностью подготовленными к продаже. Поступившие в магазин товары обычно нуждаются в ряде операций по...
-
Понятие и основные параметры конкурентоспособности продукта Проблема качества и конкурентоспособности товаров и услуг носит в современном мире...
-
Процесс и факторы ценообразования - Оценка издержек производства как основы ценообразования
Процесс ценообразования складывается из ряда последовательных этапов: 1. Выявление факторов внешней среды, влияющих на уровень цен; 2. Постановка целей...
-
Понятие и сущность конкурентоспособности В условиях рыночной экономики конкурентоспособность товара это главный фактор успеха. Конкурентоспособность...
-
Анализ факторов маркетинговой среды рынка услуг пассажирского транспорта муниципального образования
Анализ факторов маркетинговой среды рынка услуг пассажирского транспорта муниципального образования Анализ среды является важнейшим процессом...
-
Главной целью исследование потребителей в системе маркетинга становится, конечно же, определение нескольких побудительных факторов, которыми...
-
Заключение - Анализ конкурентоспособности фирмы и управление ею
В данной работе был проведен анализ оценки конкурентоспособности товаров и услуг на внутреннем рынке. Безусловно, данный анализ не полон в силу ряда...
-
На конкурентоспособность фирм, занимающихся продажей компьютеров и комплектующих к ним, влияют следующие параметры: качество, надежность, стабильность...
-
Факторы формирования ассортимента в системе товарной политики предприятия Формирование ассортимента товаров в розничных торговых предприятиях -- сложный...
-
Динамика экологическойситуации в целом негативная: 44% сообщили об ухудшении ситуации в стране и 39% - в месте проживания. Группа заявивших о...
-
Анализ внешней среды служит инструментом, при помощи которого разработчики стратегии контролируют внешние по отношению к организации факторы с целью...
Анализ факторов, обуславливающих успех управления маркетингом, Оценка значимости местонахождения пункта продаж на средние цены автомобилей - Решение исследовательских задач