Основные сведения о коде - Построение декодера Рида - Маллера
За время исследования помехоустойчивых кодов была наработана огромная теория и выстроена сложнейшая математическая база помехоустойчивого кодирования. Приведем основные понятия из этой теории.
Блоковый код мощности М над алфавитом из q символов определяется как множество из М q-ичных последовательностей длины n, называемых кодовыми словами (если q = 2, то символы называются битами).
При этом М = qK для некоторого целого k, код называется (n, k)-кодом. Причем каждой последовательности из k q-ичных символов можно сопоставить последовательность из n q-ичных символов, являющуюся кодовым словом. Имеются два основных класса кодов: блоковые коды и древовидные коды (смотри рисунок 1).
2
В теории блоковых кодов доказывается тот факт, что хорошими являются коды с большой длиной кода и очень хорошими являются коды с очень большой длиной блока.
О блоковом коде судят по трем параметрам: длине блока n, информационной длине k и минимальному кодовому расстоянию d.
Расстоянием по Хэммингу [1] между двумя q-ичными последовательностями x и y длины n называется число позиций, в которых они различны. Это расстояние обозначается через d (x, y).
Минимальным кодовым расстоянием кода [1] называется наименьшее из всех расстояний по Хэммингу между различными парами кодовых слов, т. е.
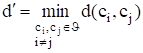
(5),
(n, k)-код с минимальным расстоянием d называется также (n, k, d)-кодом.
В более общем случае если произошло t ошибок и если расстояние от принятого слова до каждого другого кодового слова больше t, то декодер исправит эти ошибки, приняв ближайшее к принятому кодовое слово в качестве действительно принятого. Это всегда будет так, если
(6).
Геометрическая иллюстрация дается на рисунке 2. В пространстве всех q-ичных n-последовательностей выбрано некоторое множество n-последовательностей, объявленных кодовыми словами. Если d' - минимальное расстояние этого кода, а t - наибольшее целое число, удовлетворяющее условию, то вокруг каждого кодового слова можно описать непересекающуюся сферу радиуса t. Принятые слова, лежащие внутри сфер, декодируются как кодовое слово, являющееся центром
Соответствующей сферы. Если произошло не более t ошибок, то принятое слово всегда лежит внутри соответствующей сферы и декодируется правильно.
Некоторые принятые слова, содержащие более t ошибок, попадут внутрь сферы, описанной вокруг другого кодового слова, и будут декодированы неправильно. Другие принятые слова, содержащие более t ошибок, попадут в промежуточные между сферами декодирования области.
Полем [3] называется множество с двумя определенными на нем операциями - сложением и умножением, причем имеют место следующие аксиомы:
- 1) множество образует абелеву группу по сложению; 2) поле замкнуто относительно умножения, и множество ненулевых элементов образуют абелеву группу по умножению. 3) закон дистрибутивности:
- (a + b)c = ac+bc для любых a, b, c из поля.
Поле с q элементами, если оно существует, называется конечным полем, или полем Галуа [2], и обозначается через GF(q).
Линейный код образует подпространство в GF(q). Любое множество базисных векторов может быть использовано в качестве строк для построения (kn)-матрицы G, которая называется порождающей матрицей кода. Пространство строк матрицы G есть линейный код, любое кодовое слово есть линейная комбинация строк из G. Множество qK кодовых слов называется линейным (n, k)-кодом.
Строки матрицы G линейно независимы, и число строк k равно размерности подпространства. Размерность всего пространства GFN(q) может быть отображена на множество кодовых слов.
Любое взаимно однозначное соответствие k-последовательностей и кодовых слов может быть использовано для кодирования, но наиболее естественный способ кодирования использует отображение
C = iG (7),
Где i - информационное слово, представляющее собой k-последовательность кодируемых информационных символов, а c - образующая кодовое слово n-последовательность.
Например, если
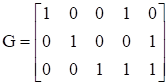
,
То информационное слово
I = [0 1 1]
Будет кодироваться в кодовое слово
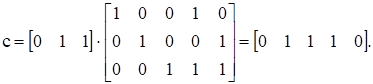
Кроме порождающей матрицы существует так же проверочная матрица называемая Н матрицей. При этом выполняется условие
СНТ=0 (8).
Матрица Н является (n - k)n матрицей; поскольку равенство сНТ = 0 выполняется при подстановке вместо с любой строки матрицы G, то
GHT = 0 (9).
Для приведенной выше порождающей матрице G, получаем
.
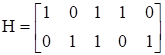
Коды Рида - Маллера представляют собой класс линейных кодов над GF(2) c простым описанием и декодированием, осуществляемым методом простого голосования. По этим причинам коды Рида - Маллера играют важную роль в кодировании (коды Рида - Маллера были использованы при передаче фотографий Марса космическим кораблем Маринер в 1972г.)[2], хотя если судить по минимальному расстоянию, то, за некоторыми исключениями, они не заслуживают особого внимания. Для любых целых m и r < m существует код Рида - Маллера r-го порядка длины 2M.
Код Рида - Маллера является линейным кодом и определяется через порождающую матрицу, которая обычно, для удобства декодирования, строится в несистематической форме. Покомпонентным произведением двух векторов a = (a0, a1, ... aN-1) и b = (b0, b1, ... bN-1) является вектор
С = (a0B0, a1B1, ... aN-1BN-1) (10).
Порождающая матрица кода Рида - Маллера r-го порядка длиной 2M определяется как совокупность блоков
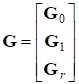
,
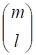
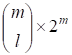
Где G0 - вектор размерности n = 2M, состоящий из одних единиц; G1 есть (m2M)-матрица, содержащая в качестве столбцов все двоичные m-последовательности; строки матрицы GL получаются из строк матрицы G1 как всевозможные произведения l строк из G1. Считается, что первый столбец в G1 состоит из одних нулей, последний - из одних единиц, а остальные m последовательности в G1 расположены в порядке возрастания, считая, что младший бит расположен в нижней строке. Существует всего способов выбора l строк, входящих в произведение, следовательно матрица GL имеет размер. Отсюда следует, что для кода Рида - Маллера порядка r
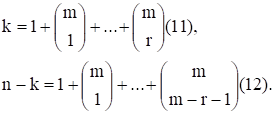
Что обеспечивается линейной независимостью строк в матрице G. Код нулевого порядка является (n, 1)-кодом. Это просто код с повторением, который тривиально декодируется с помощью мажоритарного метода. Минимальное расстояние такого кода равно 2M.
Например, возьмем m = 4, n = 16, r = 3. Тогда
,
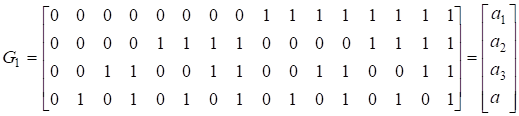
.
Поскольку G1 имеет 4 строки, матрица G2 имеет строк:
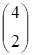
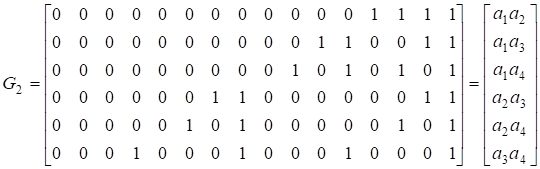
,
А матрица G3 имеет строк:
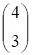
Таким образом, порождающая матрица кода Рида - Маллера третьего порядка длины 16 является (1516)-матрицей вида
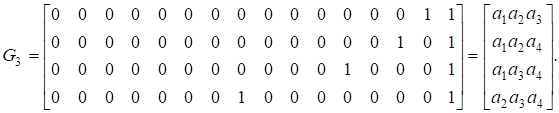
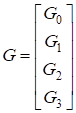
.
Эта порождающая матрица задает (16, 15)-код над GF(2) (на самом деле это просто код с проверкой на четность). Другой код Рида - Маллера может быть получен с использованием этих матриц, если взять r = 2. В этом случае порождающая матрица будет иметь вид
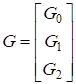
И задает (16, 11)-код над GF(2). В действительности это (15, 11)-код Хэмминга, расширенный с помощью проверки на четность.
Из определения порождающей матрицы ясно, что код Рида - Маллера r-го порядка может быть получен дополнением кода Рида - Маллера (r - 1)-го порядка, а код Рида - Маллера (r - 1)-го порядка получается из кода r-го порядка с помощью выбрасывания. Поскольку код Рида - Маллера r-го порядка содержит код (r - 1)-го порядка, ясно, что его минимальное расстояние не может быть больше минимального расстояния кода (r-1)-го порядка. Вообще, кодовое расстояние кода Рида - Маллера определяется по формуле
D = 2M - r (13).
Каждая строка матрицы G1 имеет вес 2M - l. Таким образом, любая строка матрицы G имеет четный вес, а сумма двух двоичных векторов четного веса также имеет четный вес. Следовательно все линейные комбинации строк матрицы G имеют четный вес, а это значит, что все кодовые слова имеют четный вес. Матрица GR содержит строки весом 2M - r, и, следовательно, минимальный вес кода не превосходит 2M - r.
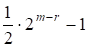
Для декодирования кодов Рида - Маллера был специально разработан алгоритм Рида [2], который позволяет исправлять ошибок и восстанавливать k информационных символов. Отсюда следует, что минимальное расстояние будет не меньше 2M - r - 1, но оно должно быть четным и потому будет не меньше 2M - r.
Поскольку код Рида - Маллера нулевого порядка можно декодировать с помощью мажоритарного метода, можно по индукции получить метод декодирования кодов Рида - Маллера высших порядков.
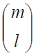
Для удобства разобьем информационный вектор на r + 1 сегмент, положив, где сегмент IL содержит информационных битов. Каждый сегмент будет умножаться на один блок матрицы G. Следовательно, кодирование можно представить поблочным умножением вектора на матрицу:
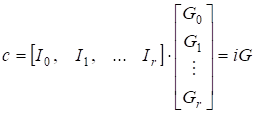
(14).
Предположим, что информационная последовательность разбита на сегменты следующим образом: каждому сегменту соответствует один из r блоков порождающей матрицы, который при кодировании умножается на этот сегмент. Если мы сможем восстановить информационные биты в r-ом сегменте, то затем сможем вычислить их вклад в принятое слово и вычесть его из принятого слова. Тогда задача сведется к декодированию кода Рида - Маллера (r - 1)-го порядка. Процедура декодирования представляет собой последовательность мажоритарных декодирований и начинается с нахождения мажоритарным методом информационных символов в сегменте м номером r.
Принятое слово запишем в виде
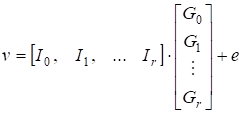
(15).
Алгоритм декодирования сначала по принятому слову восстанавливает IR, затем вычисляется разность
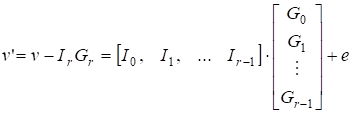
(16),
Которая является искаженным кодовым словом кода Рида - Маллера (r - 1)-го порядка.
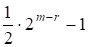
Прежде всего, рассмотрим декодирование информационного бита iK-1, который умножается на последнюю строку матрицы GR. Декодируем этот бит, вычисляя 2M - r проверочных сумм по 2R бит из 2M бит принятого слова, так что каждый принятый бит входит только в одну сумму. Проверочные суммы строятся таким образом, что символ iK-1 вносит вклад только в один бит, а все другие информационные биты вносят вклад в четное число бит в каждой проверочной сумме. Таким образом, при отсутствии ошибок все проверочные суммы равны iK-1. Но, даже если имеется не более ошибок, большинство проверочных сумм по-прежнему будет равняться iK-1.
Первая проверочная сумма представляет собой сумму по модулю 2 первых 2 бит принятого слова, вторая - сумму по модулю два вторых 2R бит принятого слова и т. д. Всего получается 2M - r проверочных сумм, и по предположению имеется ошибок. Таким образом, мажоритарное голосование проверочных сумм дает правильное значение iK-1. Для построенного ранее (16, 11)-кода Рида - Маллера эти четыре суммы выглядят следующим образом:
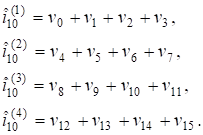
Если произошла только одна ошибка, то одна из оценок, даваемых проверочными суммами, будет неверна; мажоритарное решение дает значение i10. Если произошло две ошибки, то ни одно значение проверочных сумм не встречается чаще других и обнаруживается одна ошибка.
Аналогично может быть продекодирован любой информационный символ, который умножается на одну из строк матрицы GR. Это происходит потому, что любая строка матрицы GR ничем не выделяется среди остальных. Перестановкой столбцов мы можем добиться того, что любая строка будет выглядеть так же, как последняя строка матрицы GR. Следовательно, можно использовать те же самые проверочные суммы, соответственно переставив индексы у символов, входящих в эти суммы. После построения 2M - r проверочных сумм каждый бит декодируется мажоритарным методом.
После того как эти информационные символы найдены, их вклад в кодовое слово вычитается из принятого слова. Это эквивалентно тому, что мы получаем слово кода Рида - Маллера (r - 1)-го порядка. В свою очередь, его последний сегмент информационных бит вычисляется с помощью той же самой процедуры.
Этот процесс повторяется до тех пор, пока не будут найдены все информационные биты.
Похожие статьи
-
Заключение - Построение декодера Рида - Маллера
В этом курсовом проекте мы досконально изучили код Рида - Маллера, ознакомились с историей его открытия Ридом и Маллером, а так же краткой историей всего...
-
На выбор типа кода повлиял тот факт, что коды Рида - Маллера являются одним из наиболее старых и хорошо изученных семейств кодов. Хотя минимальное...
-
Введение - Построение декодера Рида - Маллера
В последнее время передача данных является наиболее быстро развивающейся областью техники. И это не случайно. Всем известно выражение: "Кто владеет...
-
Разработка функциональной электрической схемы декодера - Построение декодера Рида - Маллера
При разработке функциональной схемы рассмотрим каждый блок структурной схемы подробнее. Входной регистр. Входной регистр служит для приема всех бит...
-
Алгоритм работы декодера кода Рида - Маллера будем разрабатывать на основе уже приведенных выше уравнений. Алгоритм приведен на рисунке 12. В начале...
-
Принцип построения помехоустойчивых кодов - Кодек каскадного кода Хэмминга
Помехоустойчивое кодирование представляет собой процесс преобразования передаваемых информационных символов по определенному алгоритму, и в результате...
-
Разработка кодера Хемминга Кодирующее устройство предназначено для кодирования исходной последовательности информационных символов. Для того, чтобы...
-
Литература - Построение декодера Рида - Маллера
1. Блейхут Р. Теория и практика кодов, контролирующих ошибки. Москва: Мир, 1986 г. 2. Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих...
-
Основные принципы построения САПР - Состав систем автоматизированного проектирования
Разработка САПР представляет собой крупную научно-техническую проблему, а ее внедрение требует значительных капиталовложений. Накопленный опыт позволяет...
-
Структурная схема терминов Под корпоративной информационной системой (КИС или EIS - Enterprise Information System) понимают информационную систему...
-
Исходные файлы - это файлы мультимедиа (например, аудио - или видеофайлы) или изображений, которые импортируются в текущий проект. При импорте видео - и...
-
Понятие матрицы Матрицей А размером mn или просто (mn)-матрицей называют прямоугольную таблицу, содержащую m строк и n столбцов, элементами которой...
-
1. Провести обзор методов автоматического построения профиля нормального поведения веб-приложения. 2. Сформулировать требования к методу, провести...
-
Тема: "Основные устройства ЭВМ, их функции и взаимосвязь в процессе работы. Магистрально - модульный принцип построения ПЭВМ" Цель урока: Объяснить...
-
Начинать следует с определения структуры таблицы, соответствующей предметной области, т. е. с определения полей, которые надо включить в таблицу, типов...
-
Роль ключевых предложений в построении текста В первую очередь введем несколько базовых понятий рассматриваемой предметной области: текст, сложное...
-
В программе присутствуют следующие основные модули: - PlatformManager - DeviceManager - ScenariosManager - ScenarioEngine - ExportManager - ImportManager...
-
Практическая реализация - Исправление ошибок с помощью кода Рида-Соломона
Кодирование с помощью кода Рида-Соломона может быть реализовано двумя способами:систематическим и несистематическим (см. [1], описание кодировщика). При...
-
Линейные блоковые коды - Кодек каскадного кода Хэмминга
Код называется групповым, если кодовые комбинации образуют некоторую подгруппу группы всех последовательностей длиной n Линейные коды задаются с помощью...
-
Основная программа Построение интерполяционного многочлена Нахождение максимума функции методом дихотомии Вычисление значения заданной функции Создание и...
-
Для замеров производительности использовалось три запроса, представляющих три наиболее типичные проблемные рассчеты. Ниже приведены эти запросы на языке...
-
Теоретические аспекты СУБД, Основные понятия баз данных - Виды и возможности СУБД
Основные понятия баз данных В настоящее время жизнь человека настолько насыщена различного рода информацией, что для ее обработки требуется создание...
-
Основные понятия алгоритмического языка - Алгоритмический язык Pascal
СОСТАВ ЯЗЫКА. Обычный разговорный язык состоит из четырех основных элементов: символов, слов, словосочетаний и предложений. Алгоритмический язык содержит...
-
Оценка качества работы системы - Роль ключевых предложений в построении текста
Для того чтобы оценить качество работы системы, с ее помощью были составлены рефераты 40 текстов. Среди них было 20 текстов публицистического стиля...
-
Основные тенденции рынка: статистика и прогнозы Как известно, тот, кто владеет информацией, владеет миром. Однако сегодня все убедительнее звучит и...
-
В данном разделе выпускной квалификационной работы описывается процесс разработки программы извлечения КП текста, а также производится оценка качества ее...
-
Понятие автоматического реферирования текста - Роль ключевых предложений в построении текста
Реферирование является одним из основных способов анализа текстовой информации. Его конечным продуктом является реферат - "краткое изложение содержания...
-
Постановка задачи: Для заданных функций необходимо: 1. Построить электронную таблицу (одну для обеих функций) для вычисления значений функций в заданном...
-
Из основного бизнес-процесса по выполнению заказа на проектирование и конструирование РЭКа можно вынести, что производственную спецификацию проекта отдел...
-
3. Построение графиков функций - Основы информатики
3.1 Построить в разных системах координат при х Є [-3.2; -1] графики следующих функций: G = , z = , y = . Решение: Для того, чтобы построить график...
-
Сеансовый уровень, Представительный уровень - Принципы построения открытых графических систем
Сеансовый уровень (Session layer) обеспечивает управление диалогом: фиксирует, какая из сторон является активной в настоящий момент, предоставляет...
-
Сетевой уровень - Принципы построения открытых графических систем
Сетевой уровень (Network layer) служит для образования единой транспортной системы, объединяющей несколько сетей, причем эти сети могут использовать...
-
Канальный уровень - Принципы построения открытых графических систем
На физическом уровне просто пересылаются биты. При этом не учитывается, что в некоторых сетях, в которых линии связи используются (разделяются)...
-
Из универсальных языков программирования сегодня наиболее популярны следующие: Бейсик (Basic), Паскаль (Pascal), Си++ (C++), Ява (Java). Для каждого из...
-
МЕТОДОВ МЕТОД СОРТИРОВКИ Пирамидальная сортировка Пирамидальная сортировка основана на алгоритме построения пирамиды. Последовательность aI, aI+1,...,aK...
-
Основные возможности табличного процессора MS Excel
Задание 1. Необходимо Создать Лист Для Расчета Значения Выражения При Заданных Значениях A И B 1.1. Оформляем таблицу, принимаем за a и b некоторые...
-
Основные понятия и объекты - Терминалы и псевдотерминалы в Linux. Средства работы с терминалами
В стандарте POSIX-2001 Терминал или терминальное устройство определяется как символьный специальный файл, удовлетворяющий спецификациям общего...
-
В длинных документах большинство абзацев форматируется одинаково. Точнее говоря, обычно существует несколько вариантов оформления абзаца, которые...
-
Концентраторы - Построение локальных сетей по стандартам физического и канального уровней
Основные и дополнительные функции концентраторов Практически во всех современных технологиях локальных сетей определено устройство, которое имеет...
-
Общие сведения о тестировании Данный раздел посвящен проведению тестирования клиентского приложения. Тестирование для серверной части системы не...
Основные сведения о коде - Построение декодера Рида - Маллера