Определение ошибок выборочного наблюдения - Особенность использования выборочного наблюдения
При выборочном наблюдении должна быть обеспечена случайность отбора единиц. Каждая единица должна иметь равную с другими возможность быть отобранной. Именно на этом основывается собственно-случайная выборка.
К Собственно-случайной выборке Относится отбор единиц из всей генеральной совокупности (без предварительного расчленения ее на какие-либо группы) посредством жеребьевки (преимущественно) или какого-либо иного подобного способа, например, с помощью таблицы случайных чисел. Случайный отбор - это отбор не беспорядочный. Принцип случайности предполагает, что на включение или исключение объекта из выборки не может повлиять какой-либо фактор, кроме случая. Примером собственно-случайного отбора могут служить тиражи выигрышей: из общего количества выпущенных билетов наугад отбирается определенная часть номеров, на которые приходятся выигрыши. Причем всем номерам обеспечивается равная возможность попадания в выборку. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки.
Доля выборки Есть отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности. Так, при 5 %-й выборке из партии деталей в 1000 ед. объем выборки составляет 50 ед., а при 10 %-й выборке - 100 ед. и т. д. При правильной научной организации выборки ошибки репрезентативности можно свести к минимальным значениям, в результате - выборочное наблюдение становится достаточно точным.
Собственно-случайный отбор "в чистом виде" применяется в практике выборочного наблюдения редко, но он является исходным среди всех других видов отбора, в нем заключаются и реализуются основные принципы выборочного наблюдения.
Рассмотрим некоторые вопросы теории выборочного метода и формулы ошибок для простой случайной выборки.
Применяя выборочный метод в статистике, обычно используют два основных вида обобщающих показателей: среднюю величину количественного признака и относительную величину альтернативного признака (долю или удельный вес единиц в статистической совокупности, которые отличаются от всех других единиц этой совокупности только наличием изучаемого признака).
Выборочная доля или частость, определяется отношением числа единиц, обладающих изучаемым признаком, к общему числу единиц выборочной совокупности:
Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.
Ошибка выборки Или, иначе говоря, ошибка репрезентативности представляет собой разность соответствующих выборочных и генеральных характеристик.
Ошибка выборки свойственна только выборочным наблюдениям. Чем больше значение этой ошибки, тем в большей степени выборочные показатели отличаются от соответствующих генеральных показателей.
Выборочная средняя и выборочная доля по своей сути являются случайными величинами, которые могут принимать различные значения в зависимости от того, какие единицы совокупности попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок - среднюю ошибку выборки.
При соблюдении принципа случайного отбора средняя ошибка выборки определяется прежде всего объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Охватывая выборочным обследованием все большее количество единиц генеральной совокупности, все более точно характеризуем всю генеральную совокупность.
Средняя ошибка выборки также зависит от степени варьирования изучаемого признака. Степень варьирования, как известно, характеризуется дисперсией или - для альтернативного признака. Чем меньше вариация признака, а следовательно, и дисперсия, тем меньше средняя ошибка выборки, и наоборот. При нулевой дисперсии (признак не варьирует) средняя ошибка выборки равна нулю, т. е. любая единица генеральной совокупности будет совершенно точно характеризовать всю совокупность по этому признаку.
Зависимость средней ошибки выборки от ее объема и степени варьирования признака отражена в формулах, с помощью которых можно рассчитать среднюю ошибку выборки в условиях выборочного наблюдения, когда генеральные характеристики неизвестны.
Поскольку практически дисперсия признака в генеральной совокупности точно неизвестна, на практике пользуются значением дисперсии ,Рассчитанным для выборочной совокупности на основании закона больших чисел, согласно которому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.
Однако дисперсия выборочной совокупности не равна дисперсии генеральной совокупности, и следовательно, средние ошибки выборки, будут приближенными. Но в теории вероятностей доказано, что генеральная дисперсия выражается через выборную следующим соотношением:
N/(n-1),
Где - величина, близкая к единице, то можно принять, что , И только в случаях малой выборки (когда объем выборки не превышает 30) необходимо учитывать коэффициент и исчислять среднюю ошибку малой выборки по формуле:
М. в = ,

Где м. в - средняя ошибка малой выборки;
- общее число единиц.
При случайном бесповторном отборе в приведенные выше формулы расчета средних ошибок выборки необходимо подкоренное выражение умножить на , Поскольку в процессе бесповторной выборки сокращается численность единиц генеральной совокупности. Следовательно, для бесповторной выборки расчетные формулы средней ошибки выборки примут вид:
,
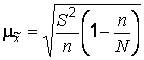
Для средней количественного признака;
,
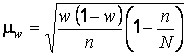
Для доли (альтернативного признака);
Так как всегда меньше, то дополнительный множитель всегда будет меньше единицы. Отсюда следует, что средняя ошибка при бесповторном отборе всегда будет меньше, чем при повторном. В то же время при сравнительно небольшом проценте выборки этот множитель близок к единице (например, при 5 % - й выборке он равен 0,95; при 2 % - й - 0,98 и т. д.). Поэтому иногда на практике пользуются для определения средней ошибки выборки формулами (1.5) и (1.6) без указанного множителя, хотя выборку и организуют как бесповторную. Это имеет место в тех случаях, когда число единиц генеральной совокупности неизвестно или безгранично, или когда очень мало по сравнению с, и по существу, введение дополнительного множителя, близкого по значению к единице, практически не повлияет на значение средней ошибки выборки.
Механическая выборка состоит в том, что отбор единиц в выборочную совокупность из генеральной, разбитой по нейтральному признаку на равные интервалы (группы), производится таким образом, что из каждой такой группы в выборку отбирается лишь одна единица. Чтобы избежать систематической ошибки, отбираться должна единица, которая находится в середине каждой группы.
При организации механического отбора единицы совокупности предварительно располагают (обычно в списке) в определенном порядке (например, по алфавиту, местоположению, в порядке возрастания или убывания значений какого-либо показателя, не связанного с изучаемым свойством, и т. д.), после чего отбирают заданное число единиц механически, через определенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки. Так, при 2 % - й выборке отбирается и проверяется каждая 50 - я единица (1 : 0,02), при 5 % - й выборке - каждая 20 - я единица (1 : 0,05), например, сходящая со станка деталь. экономический статистический комбинированный выборка
При достаточно большой совокупности механический отбор по точности результатов близок к собственно-случайному.
Для отбора единиц из неоднородной совокупности применяется, так называемая типическая выборка, Которая используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных, однотипных групп по признакам, влияющим на изучаемые показатели.
При обследовании предприятий такими группами могут быть, например, отрасль и подотрасль, формы собственности. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.
Типическая выборка обычно применяется при изучении сложных статистических совокупностей. Например, при выборочном обследовании семейных бюджетов рабочих и служащих в отдельных отраслях экономики, производительности труда рабочих предприятия, представленных отдельными группами по квалификации.
Типическая выборка дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность. Типизация генеральной совокупности обеспечивает репрезентативность такой выборки, представительство в ней каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки.
При определении средней ошибки типической выборки в качестве показателя вариации выступает средняя из внутригрупповых дисперсий.
Среднюю ошибку типической выборки Находят по формулам:
,

,
,
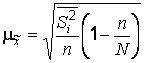
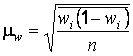
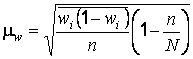
,
Где - Средняя из внутригрупповых дисперсий по выборочной совокупности;
- средняя из дисперсий доли по выборочной совокупности.
Серийная выборка Предполагает случайный отбор из генеральной совокупности не отдельных единиц, а их равновеликих групп (гнезд, серий) с тем, чтобы в таких группах подвергать наблюдению все без исключения единицы
Применение серийной выборки обусловлено тем, что многие товары для их транспортировки, хранения и продажи упаковываются в пачки, ящики и т п. Поэтому при контроле качества упакованного товара рациональнее проверить несколько упаковок (серий), чем из всех упаковок отбирать необходимое количество товара.
Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка выборки (при отборе равновеликих серий) зависит только от межгрупповой (межсерийной) дисперсии.
Среднюю ошибку выборки для средней количественного признака при серийном отборе находят по формулам:
,
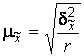
,
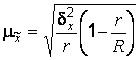
Где - Число отобранных серий,
- общее число серий.
Средняя ошибка выборки для доли (альтернативного признака) при серийном отборе:
;
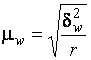
,
,
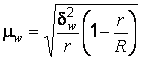
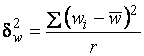
Где - доля признака в - й серии;
- общая доля признака во всей выборочной совокупности.
В практике статистических обследований помимо рассмотренных ранее способов отбора применяется их комбинация (комбинированный отбор).
Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе выборочных результатов. Выборочные средние и относительные величины распространяют на генеральную совокупность с учетом предела их возможной ошибки.
В каждой конкретной выборке расхождение между выборочной средней и генеральной, т. е. Может быть меньше средней ошибки выборки, равно ей или больше ее. Причем каждое из этих расхождений имеет различную вероятность (объективную возможность появления события). Поэтому фактические расхождения между выборочной средней и генеральной Можно рассматривать как некую предельную ошибку, связанную со средней ошибкой и гарантируемую с определенной вероятностью .
Предельную ошибку выборки для средней () при повторном отборе можно рассчитать по формуле:
= ,
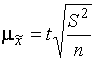
Где - нормированное отклонение - "коэффициент доверия", зависящий от вероятности, с которой гарантируется предельная ошибка выборки.
Аналогичным образом может быть записана формула предельной ошибки выборки для доли () при повторном отборе:
,
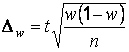
Где - предельная ошибка выборки для доли;
- нормированное отклонение.
Формула предельной ошибки выборки вытекает из основных положений теории выборочного метода, сформулированных в ряде теорем теории вероятностей, отражающих закон больших чисел.
На основании теоремы П. Л. Чебышева (с уточнениями А. М. Ляпунова) с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом объеме выборки и ограниченной генеральной дисперсии выборочные обобщающие показатели (средняя, доля) будут сколь угодно мало отличаться от соответствующих генеральных показателей.
Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью.
Из этой теоремы следует, что при достаточно большом числе независимых наблюдений, распределение выборочных средних (а следовательно, и их отклонений от генеральной средней) приближенно нормально. Распределение выборочных средних будет являться нормальным (или приближаться к нему по мере увеличения объема выборки) даже в случаях, когда генеральная совокупность имеет иную форму распределения.
Значения функции при различных значениях как коэффициента кратности средней ошибки выборки, определяются на основе специально составленных таблиц.
Предельная ошибка выборки отвечает на вопрос о точности выборки с определенной вероятностью, значение которой определяется коэффициентом (в практических расчетах, как правило, заданная вероятность не должна быть менее 0,95). Так, при = 1 предельная ошибка составит, следовательно, с вероятностью 0,683 можно утверждать, что разность между выборочными и генеральными показателями не превысит одной средней ошибки выборки. Другими словами, в 68,3% случаев ошибка репрезентативности не выйдет за пределы. При = 2 с вероятностью 0,954 она не выйдет за пределы 2, при = 3 с вероятностью 0,997 - за пределы 3 и т. д.
Как видно из приведенных выше значений функции , вероятность появления ошибки, равной или большей утроенной средней ошибки выборки, т. е. , крайне мала и равна 0,003. Такие маловероятные события считаются практически невозможными, а потому величину можно принять за предел возможной ошибки выборки.
Выборочное наблюдение проводится в целях распространения выводов, полученных по данным выборки, на генеральную совокупность. Одной из основных задач является оценка по данным выборки исследуемых характеристик (параметров) генеральной совокупности.
Наряду с абсолютным значением предельной ошибки выборки рассчитывается и предельная относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:
,
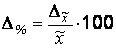
,
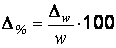
Определение необходимого объема выборки. При проектировании выборочного наблюдения с заранее заданным значением допустимой ошибки выборки очень важно правильно определить численность (объем) выборочной совокупности, которая с определенной вероятностью обеспечит заданную точность результатов наблюдения. Формулы для определения необходимой численности выборки легко получить непосредственно из формул ошибок выборки.
Так, из формул предельной ошибки выборки для повторного отбора нетрудно (предварительно возведя в квадрат обе части равенства) выразить необходимую численность выборки:
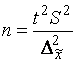
,
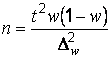
,
Эти формулы показывают, что с увеличением предполагаемой ошибки выборки значительно уменьшается необходимый объем выборки.
Для расчета объема выборки нужно знать дисперсию. Она может быть заимствована из проводимых ранее обследований данной или аналогичной совокупности, а если таковых нет, тогда для определения дисперсии надо провести специальное выборочное обследование небольшого объема.
Похожие статьи
-
Основная задача выборочного наблюдения состоит в том, чтобы на основе характеристик выборочной совокупности (например, средней) получить достоверные...
-
Ошибки выборочного наблюдения - Особенность использования выборочного наблюдения
При любом наблюдении могут происходить ошибки при регистрации единиц. В зависимости от объекта, субъекта и способа наблюдения эти ошибки могут возникнуть...
-
Понятие выборочного наблюдения - Особенность использования выборочного наблюдения
При сплошном наблюдении - множество всех единиц данной совокупности носит название генеральной совокупности. Средняя арифметическая какого-либо признака,...
-
Каждая единица при выборочном наблюдении должна иметь равную с другими возможность быть отобранной - это является основой собственно-случайной выборки....
-
Виды выборочного наблюдения - Особенность использования выборочного наблюдения
По способу отбора (способу формирования) выборки единиц из генеральной совокупности распространены следующие виды выборочного наблюдения: - простая...
-
Выборочное наблюдение - это метод статистического исследования, при котором обобщающие показатели совокупности устанавливаются только по отдельно взятой...
-
Понятие и задачи выборочного наблюдения - Методы расчета валового внутреннего продукта
Выборочное наблюдение - это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная...
-
Введение - Особенность использования выборочного наблюдения
Изучение статистических совокупностей, состоящих из множеств единиц, связано с большими трудовыми и материальными затратами. С давних пор представлялось...
-
Понятие о выборочном наблюдении Первым этапом статистического наблюдения является наблюдение. Этот этап может осуществляться сплошным и несплошным...
-
Виды и схемы отбора единиц в выборочную совокупность - Программа статистического наблюдения
Существует три основных способа отбора единиц совокупности при выборочном наблюдении: случайный, механический и типический. Случайный отбор, когда...
-
Рассмотрим некоторые формулы ошибок для разных видов выборки. Применяя выборочный метод в статистике, обычно используют дна основных вида обобщающих...
-
Одна из зада, решаемая на основе выборочного метода определение ошибки выборки. В статистике принято определять среднюю предельную и относительную ошибки...
-
Понятие малой выборки - Программа статистического наблюдения
Под малой выборкой понимается такое выборочное наблюдение, численность единиц которого не превышает 30. При оценке результатов малой выборки величина...
-
Для построения статистических группировок нужно выбрать группировочный признак, далее определить количество групп, на которые разбивают изучаемую...
-
Заключение, Список использованных источников - Особенность использования выборочного наблюдения
Переход к рыночной экономике в значительной мере способствует расширению сферы использования выборочного наблюдения. Проблемы применения конкретных видов...
-
Классификация видов статистического наблюдения - Виды статического наблюдения
В зависимости от задач статистического исследования и характера изучаемого явления учет фактов можно производить: систематически, постоянно охватывая...
-
Средняя арифметическая является наиболее распространенным видом средних величин. Она бывает двух видов: средняя арифметическая простая и средняя...
-
Отбор единиц при использовании собственно-случайной выборки предполагает непреднамеренный отбор единиц генеральной совокупности в выборочную. При этом...
-
Коммерческий недвижимость стоимость рыночный Недвижимость служит базой для хозяйственной деятельности и развития предприятий и организаций всех форм...
-
Расчет стоимости объекта сравнительным подходом продаж производился путем внесения корректировок к ценам предложения или продажи объектов-аналогов на...
-
Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что...
-
Эмпирическое корреляционное отношение измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Эмпирическое...
-
Статистическое наблюдение, его основные виды - Методы расчета валового внутреннего продукта
Статистическое наблюдение -- это массовое ( оно охватывает большое число случаев проявления исследуемого явления для получения правдивых статистических...
-
Методика построения аналитической группировки - Программа статистического наблюдения
Важная задача при построении аналитической группировки - выбор числа групп, на которые необходимо разбить изучаемую совокупность единиц наблюдения, и...
-
В краткосрочном периоде часть ресурсов остается неизменной, а часть меняется для увеличения или сокращения совокупного выпуска. В соответствии с этим...
-
Определение и классификация теневой экономики История возникновения теневой экономики начинается в 1930-е годах в США. Итальянская мафия своей...
-
Подход к оценке по доходу основывается на принципе ожидания, согласно которому все стоимости сегодня являются отражением будущих преимуществ. При...
-
Недвижимость как объект оценки. Принципы оценки недвижимости Понятие "недвижимое имущество" впервые сформулировано в римском праве в связи с введением в...
-
Основным принципом, на котором основывается затратный подход к оценке, является принцип замещения, который гласит, что осведомленный покупатель никогда...
-
В практике оценки существует три подхода к оценке коммерческой недвижимости: --затратный подход; --сравнительный подход; --доходный подход [26, c.56]. К...
-
Приобретаемый инвестором объект недвижимости допускает Альтернативные варианты его использования. В нем могут размещаться, как торговые, так и офисные,...
-
Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий,...
-
Для снижения трудоемкости расчетов используются основные свойства ср. арифм-кой: 1. Если все варианты усредняемого признака увеличить/уменьшить на...
-
Для оценки влияния факторов, определяющих вариацию, используют прием группировки: совокупность разбивают на группы, выбрав в качестве группировочного...
-
Успех дела сбора качественных и полных исходных данных с учетом требования экономного расходования материальных, трудовых и финансовых ресурсов во многом...
-
Способы расчета дисперсии - Методы расчета валового внутреннего продукта
Расчет дисперсии по преобразованной формуле, суть составления формулы. Дисперсия (уІ ) признака представляйI собой средний квадрат отклонений вариаиювог...
-
Наряду со случайным отбором применяется механический отбор. При этом способе генеральная совокупность делится на столько групп, сколько единиц наблюдения...
-
Актуальность темы исследования. После перехода Российской Федерации к рыночной модели экономики возродились права частной собственности и свобода...
-
Индустрия гостеприимства органически вписывается в рамки изменений, произошедших в экономике развитых стран, по отношению к которым все чаще...
-
Характеристика объекта оценки и внешних факторов, влияющих на его стоимость Оцениваемое нежилое помещение находится на 3 этаже в многоквартирном...
Определение ошибок выборочного наблюдения - Особенность использования выборочного наблюдения